QeRL: Beyond Efficiency – Quantization-enhanced Reinforcement Learning for LLMs
-
ArXiv URL: http://arxiv.org/abs/2510.11696v1
-
作者: Sifei Liu; Wei Huang; Huizi Mao; Song Han; Hanrong Ye; Hongxu Yin; Yao Lu; Shuai Yang; Xiaojuan Qi; Yujun Lin; 等13人
-
发布机构: HKU; MIT; NVIDIA; Tsinghua University
TL;DR
本文提出了QeRL,一个量化增强的强化学习框架,它通过利用量化噪声来提升策略探索,在显著加速大模型强化学习(RL)训练、降低显存占用的同时,实现了超越16位基线方法的性能。
关键定义
- QeRL (Quantization-enhanced Reinforcement Learning):一种为大语言模型设计的、结合了量化与强化学习的训练框架。它通过将高效的4位量化格式(如NVFP4)与低秩适应(Low-Rank Adaptation, LoRA)相结合,不仅提升了RL训练的效率,还创新性地利用量化引入的噪声来增加策略熵,从而促进模型在训练初期进行更广泛的探索。
- AQN (Adaptive Quantization Noise):自适应量化噪声。这是QeRL中提出的一个核心机制,旨在将静态的、确定性的量化噪声转变为动态的、可控的探索工具。它通过在训练过程中注入可调整的随机噪声,并使用指数衰减调度器动态控制噪声强度,从而在探索(高噪声)和利用(低噪声)之间取得平衡。
- NVFP4:一种先进的4位浮点量化格式。它采用一个全局FP32缩放因子和一组块级FP8(E4M3格式)缩放因子,支持在现代GPU(如NVIDIA Hopper和Blackwell架构)上进行硬件加速,其推理速度远超常用于QLoRA的NF4格式。
相关工作
当前,通过强化学习(RL)提升大语言模型(LLM)的复杂推理能力是研究热点,但面临严峻的资源挑战。RL训练过程(尤其是其中的 rollout 阶段)需要巨大的GPU显存和漫长的计算时间。
现有的优化方法存在以下瓶颈:
- 参数高效微调 (PEFT):如LoRA等方法虽然减少了可训练参数量,但并未解决 rollouts 阶段的计算瓶颈,因为模型主干的权重矩阵仍然是高精度的。
- 量化Rollout模型:如FlashRL等方法使用低精度模型加速 rollouts,但会导致与高精度策略模型之间的精度不匹配,需要通过重要性采样进行校正,这反而要求同时在内存中保留两个模型,增加了显存开销。
- QLoRA (使用NF4量化):直接在RL中使用QLoRA会使 rollouts 速度降低1.5-2倍,因为NF4格式需要软件层面的解包和查表操作,无法利用硬件加速,从而降低了效率。
本文旨在解决上述问题,即如何在不牺牲甚至提升性能的前提下,大幅提高LLM进行强化学习训练的效率(包括速度和显存占用)。
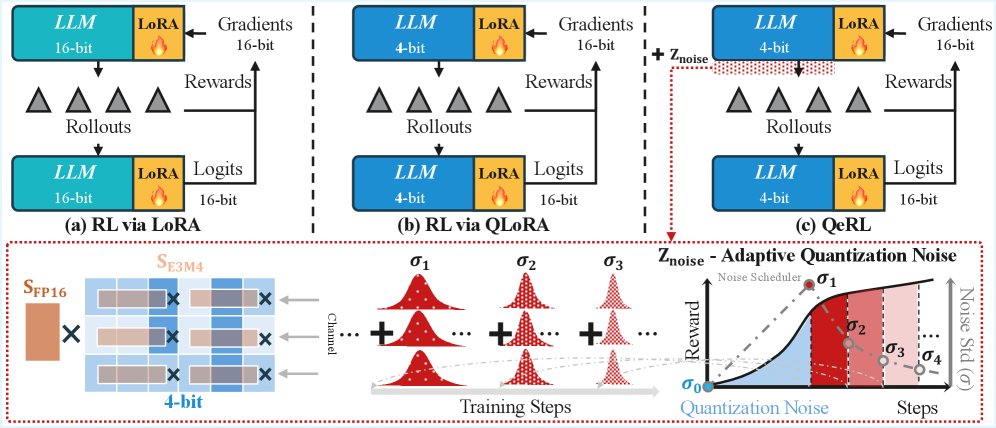
上图展示了QeRL与其他方法的对比。(a) LoRA减少了可训练参数,但未解决rollout瓶颈。(b) QLoRA(NF4+LoRA)虽然实现了量化,但速度较慢。(c) QeRL(NVFP4+LoRA)结合了自适应量化噪声(AQN),在降低显存和加速RL的同时,通过动态调整噪声增强探索,达到了与全参数微调相当的性能。
本文方法
核心思想:化噪声为优势
本文的核心洞察在于,量化过程中产生的误差(即量化噪声)并非纯粹的负面影响,反而可以被利用来促进RL中的探索。传统观点认为量化会损害模型性能,但在RL场景下,这种噪声增加了策略的熵 (entropy),使输出的概率分布更平滑,从而鼓励模型探索更多样的动作(即Token),避免过早陷入局部最优。

上图显示,量化噪声带来了更高的初始熵,这鼓励了RL训练中的探索,从而加速了奖励的增长。
QeRL训练框架
QeRL建立在主流的LLM策略优化算法之上,如GRPO和DAPO。其基本框架如下:
- 模型主体量化:将LLM的主干权重使用高性能的NVFP4格式进行4位量化。这得益于Marlin等内核的优化,能够在现代GPU上实现极快的矩阵运算,从而大幅加速了RL中最为耗时的 rollouts 和 prefilling 阶段。
- 低秩适应训练:在量化的主干权重之上,叠加LoRA层。在训练过程中,仅更新LoRA矩阵 \(A\) 和 \(B\) 的参数,而量化的主干权重保持冻结。
量化如何促进探索
量化操作可以被建模为给模型参数引入了固定的噪声 \(Δε\):
\[(\tilde{\theta}+\theta_{lora})-(\theta+\theta_{lora})=Q(\theta)-\theta=\Delta\epsilon\]| 其中 \(Q(θ)\) 是反量化后的权重。这个噪声 \(Δε\) 会在网络的前向传播中逐层累积,扰动最终的logits输出,使得模型在softmax后的概率分布更加平坦,即策略熵 $$H(π(· | q))$$ 增加。这类似于在RL中向参数空间注入噪声以驱动探索的经典方法。 |
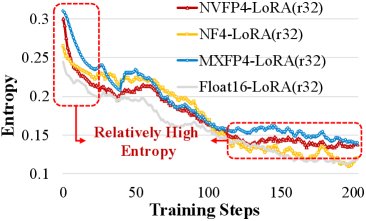
上图对比了不同量化格式下模型的策略熵。可以看到,量化模型的熵显著高于16位模型。

上图展示了不同量化方法在DAPO和GRPO算法下的训练奖励曲线。尽管MXFP4在训练早期得分更高,但NVFP4最终收敛到更好的奖励。
自适应量化噪声 (AQN)
静态的量化噪声在训练后期可能会阻碍模型收敛到最优策略。为解决此问题,本文提出了AQN机制,将噪声变为动态可控。
-
噪声注入:在每个前向传播中,向模型的激活值引入一个随机噪声向量 \(Z_noisy\),其方差 \(σ\) 可控。
\[\Delta\epsilon^{\prime}=\mathbf{Z}_{\text{noisy}}+\Delta\epsilon=\mathbf{Z}_{\text{noisy}}+\left(\hat{\mathbf{W}}-\mathbf{W}\right)\] -
噪声调度:在训练过程中,使用指数衰减调度器逐步减小噪声的尺度 \(σ\)。训练初期使用较大的噪声以鼓励探索,后期则减小噪声以帮助模型稳定收敛和利用。
\[\sigma(k)=\sigma_{\text{start}}\cdot\left(\frac{\sigma_{\text{end}}}{\sigma_{\text{start}}}\right)^{\frac{k-1}{K-1}}\] -
零开销实现:为了避免引入额外参数和计算开销,AQN巧妙地将噪声向量 \(Z_noisy\) 合并到层归一化(Layer Normalization,如RMSNorm)的可学习缩放参数 \(w\) 中。通过数学变换,对输入的加性噪声可以等效地转化为对权重矩阵的乘性噪声,而无需修改高效的量化计算内核。
\[\operatorname{RMSNorm}_{\text{noise}}(\mathbf{x})=\mathbf{w}_{\text{noise}}\odot\frac{\mathbf{x}}{\sqrt{\frac{1}{N}\sum^{N}_{i=1}x_{i}^{2}+\delta}},\quad \mathbf{w}_{\text{noise}}=\mathbf{Z}_{\text{noise}}+\mathbf{w}\]
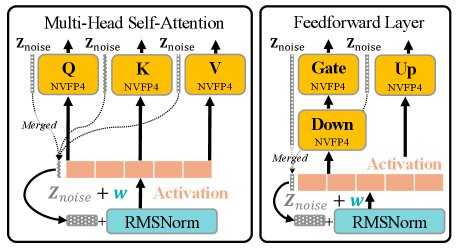
上图展示了AQN的部署方案,噪声向量 \(Z_noise\) 被整合到每个Transformer块的层归一化(如RMSNorm)中。
实验结论
效率与性能
实验结果表明,QeRL在效率和性能上均取得了显著优势。
- 效率:在 rollouts 阶段,QeRL实现了超过1.5倍的速度提升。它成功地在单张H100 80GB GPU上完成了32B模型的RL训练,而显存占用仅为16位LoRA的40-50%。
- 性能:
- 在GSM8K基准上,QeRL训练的7B模型得分达到90.8%,超越了16-bit LoRA(88.1%)和QLoRA(85.0%),并与全参数微调的性能(91.2%)相当。
- 在更具挑战性的BigMath数据集和多个数学推理基准(MATH 500, AIME, AMC)上,QeRL的表现也持续优于或持平于16-bit LoRA,甚至在某些情况下(如14B模型在AMC 23上的表现)超越了全参数微调。
下表展示了在GSM8K数据集上使用GRPO算法的训练结果。QeRL (w/ AQN) 行代表本文提出的完整方法。
(a) Qwen2.5-3B-Instruct 在 GSM8K 上的性能
| 模型 | 方法 | 精度 | GSM8K (Pass@1) |
|---|---|---|---|
| Qwen2.5-3B-Instruct | - | BF16 | 61.2 |
| - | NF4 | 57.5 (-3.7) | |
| - | MXFP4 | 59.8 (-1.4) | |
| - | NVFP4 | 59.4 (-1.8) | |
| Full | BF16 | 84.4 (+23.2) | |
| LoRA | BF16 | 76.1 (+14.9) | |
| LoRA (QLoRA) | NF4 | 76.1 (+14.9) | |
| LoRA | MXFP4 | 73.4 (+12.2) | |
| LoRA (QeRL) | NVFP4 | 83.3 (+22.2) | |
| LoRA (QeRL w/ AQN) | NVFP4 | 83.7 (+22.6) |
(b) Qwen2.5-7B-Instruct 在 GSM8K 上的性能
| 模型 | 方法 | 精度 | GSM8K (Pass@1) |
|---|---|---|---|
| Qwen2.5-7B-Instruct | - | BF16 | 76.3 |
| - | NF4 | 70.5 (-5.8) | |
| - | MXFP4 | 71.3 (-5.0) | |
| - | NVFP4 | 73.4 (-2.9) | |
| Full | BF16 | 91.2 (+14.9) | |
| LoRA | BF16 | 88.1 (+11.8) | |
| LoRA (QLoRA) | NF4 | 85.0 (+8.7) | |
| LoRA | MXFP4 | 86.4 (+10.1) | |
| LoRA (QeRL) | NVFP4 | 88.5 (+12.2) | |
| LoRA (QeRL w/ AQN) | NVFP4 | 90.8 (+13.5) |
训练动态与消融研究
- 更快的奖励增长:实验图表显示,QeRL在训练初期(约200步内)就实现了奖励的快速增长,而基线方法则需要更长时间(超过500步),这验证了量化噪声能有效促进早期探索。
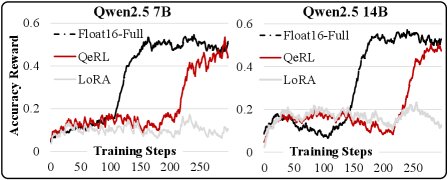
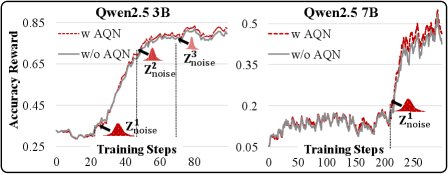
- AQN的有效性:消融实验证明了AQN机制的价值。带有AQN的QeRL比仅使用静态量化噪声的QeRL取得了更高的最终性能。在多种噪声衰减函数中,指数衰减函数在训练后期表现出更稳定的性能提升。
总结
本文提出的QeRL框架成功地证明了量化不仅可以作为提升LLM强化学习效率的工具,还能通过其内生的、可控的噪声机制,成为增强模型探索能力、提升最终性能的有效手段。这一发现为未来大模型的高效训练和优化开辟了新的方向。