Qwen2.5-Math Technical Report: Toward Mathematical Expert Model via Self-Improvement

TL;DR

本文提出了一系列数学专用大语言模型 Qwen2.5-Math，其核心创新在于将“自我改进”（self-improvement）的理念贯穿于从预训练、后训练到推理的整个模型开发流程，从而在多个数学基准上实现了超越现有开源及闭源模型（如GPT-4o）的顶尖性能。

关键定义

相关工作

当前，通用大语言模型由于在预训练阶段缺乏足够的数学相关数据，其数学推理能力普遍存在不足。尽管先前已有研究（如 Minerva、DeepSeekMath）证明，通过构建大规模的数学专业语料库进行持续预训练是提升模型数学能力的有效途径，但该领域仍面临两大关键瓶ăpadă颈：

  1. 高质量数据的稀缺性：如何自动且大规模地生成高质量、高可靠性且覆盖多种推理形式（如CoT和TIR）的训练数据，是提升模型能力的核心挑战。
  2. 对齐与优化的复杂性：如何高效地利用这些数据，通过监督微调和强化学习，使模型的推理过程与正确解题路径对齐，并持续优化其性能，仍是亟待解决的问题。

本文旨在解决上述问题，通过一套系统性的“自我改进”流程，不仅提升模型在英、中文数学问题上的推理能力，尤其是在高难度问题上的表现，同时也探索出一条不完全依赖模型参数规模扩张的性能提升路径。

本文方法

本文提出了一套从 Qwen2-Math 演进至 Qwen2.5-Math 的完整开发流程，其核心是“自我改进”理念在预训练和后训练阶段的系统性应用。

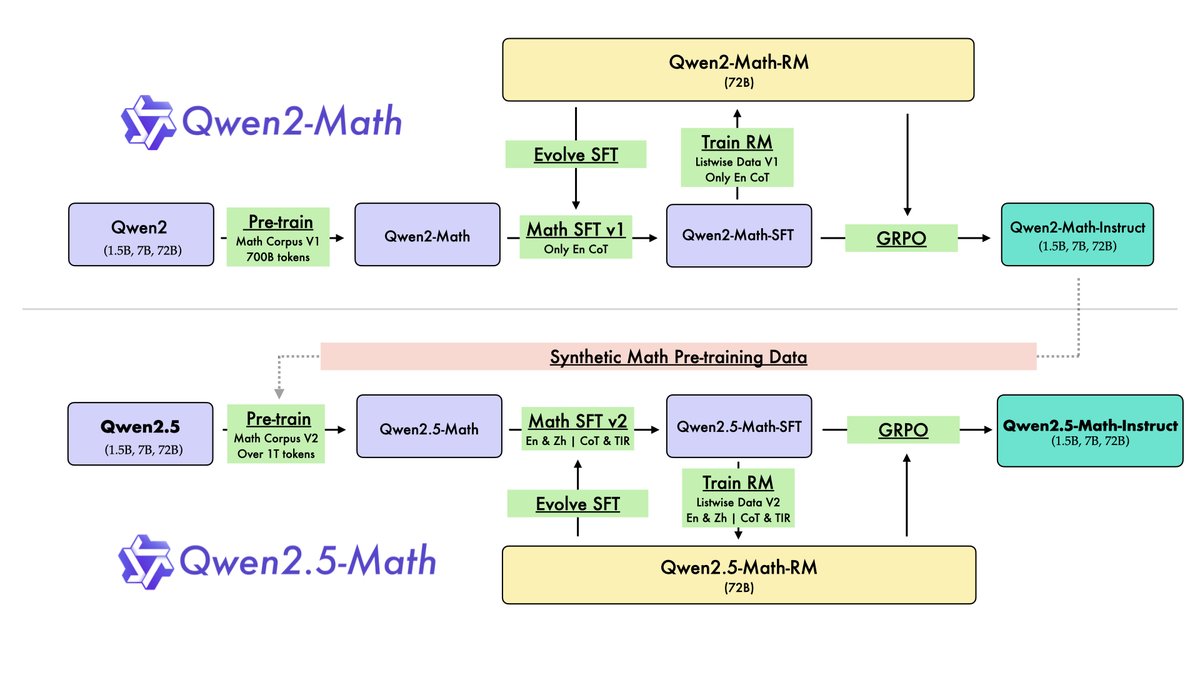Qwen2-Math 和 Qwen2.5-Math 的开发流程图 图注：Qwen2-Math 和 Qwen2.5-Math 的开发流程。

预训练阶段：基于自我改进的数据增强

预训练的目标是构建一个富含数学知识的高质量数据集。相比于 Qwen2-Math 使用的 Qwen Math Corpus v1 (700B token)，Qwen2.5-Math 的预训练采用了升级版的 Qwen Math Corpus v2 (超过 1T token)。其增强主要来自三个方面：

  1. 自我数据合成：利用上一代性能最强的 Qwen2-Math-72B-Instruct 模型，大规模地合成新的高质量数学预训练数据。
  2. 数据源扩充：收集了更多高质量的数学数据，特别是来自网页、书籍和代码库的中文数学内容。
  3. 更强的基座模型：Qwen2.5-Math 的预训练不再从 Qwen2 系列初始化，而是从语言、代码和推理能力更强的 Qwen2.5 通用系列模型开始，再使用 Qwen Math Corpus v2 进行持续预训练。

通过在数据集和基座模型上的双重改进，Qwen2.5-Math 的基础数学能力得到了显著提升。

后训练阶段：SFT、RM与RL的迭代循环

后训练阶段旨在进一步增强模型在思维链（CoT）和工具集成推理（TIR）上的逻辑推理能力，该阶段包含监督微调、奖励模型训练和强化学习三个紧密相连的环节。

监督微调 (Supervised Fine-tuning, SFT)

本文为 CoT 和 TIR 两种模式分别构建了专用的 SFT 数据集。

奖励模型 (Reward Model, RM) 训练

为了在最终答案之外提供更细粒度的监督信号，本文训练了一个数学专用的奖励模型 Qwen2.5-Math-RM。

\[\mathcal{L}_{rm}(\theta)=-\frac{1}{k\times(6-k)}E_{(x,y_{pos},y_{neg})\sim D} \left[\log\left(\sigma\left(r_{\theta}(x,y_{pos})-r_{\theta}(x,y_{neg})\right)\right)\right].\]

其中，$r_{\theta}(x,y)$ 是奖励模型的输出，$k$ 是正样本数量。

强化学习 (Reinforcement Learning, RL)

在 SFT 之后，本文采用 RL 进一步优化模型。

\[\begin{aligned} \mathcal{J}_{GRPO}(\theta) &= \mathbb{E}_{[q\sim P(Q),\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old}}(O \mid q)]} \\ & \quad \frac{1}{G}\sum_{i=1}^{G}\frac{1}{ \mid o_{i} \mid }\sum_{t=1}^{ \mid o_{i} \mid }\{ \min[\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_{old}}^{i,t}}\hat{A}_{i,t},\textrm{clip}(\frac{\pi_{\theta}^{i,t}}{\pi_{\theta_{old}}^{i,t}},1-\epsilon,1+\epsilon)\hat{A}_{i,t}]-\beta\mathbb{D}_{KL}[\pi_{\theta} \mid \mid \pi_{\textrm{ref}}]\}, \end{aligned}\] \[r=\sigma(\alpha\cdot r_{m})+(r_{v}-1),\]

其中 $r_m$ 是 RM 的分数，$r_v \in {0, 1}$ 是验证器结果，$\alpha=0.5$。这种设计确保了最终答案正确的回答总能获得更高的奖励。

数据去污

为保证评估的公正性，本文实施了严格的数据去污流程。使用 13-gram 匹配结合文本归一化来识别和过滤训练数据中与测试集重叠或高度相似的样本。特别地，本文还排除了那些与测试题在概念或结构上高度相似但非完全重复的问题，以避免“隐性”泄露。

MATH 训练集中的问题 (已过滤) MATH 测试集中的问题
$1+2+3+4+\dots+9+10$ 除以 8 的余数是多少？ $1+2+3+4+\dots+9+10$ 除以 9 的余数是多少？
在 1 到 1000（含）之间，有多少个整数 $n$ 使得 $\frac{n}{1400}$ 的小数表示是有限的？ 在 1 到 1000（含）之间，有多少个整数 $n$ 使得 $\frac{n}{1375}$ 的小数表示是有限的？
Krista 周日早上在新存钱罐里存了 1 分钱。周一存了 2 分，周二存了 4 分，并持续两周每天存入的钱翻倍。在哪一天，她存钱罐里的总金额首次超过 2 美元？ Krista 周日早上在新存钱罐里存了 1 分钱。周一存了 2 分，周二存了 4 分，并持续两周每天存入的钱翻倍。在哪一天，她存钱罐里的总金额首次超过 5 美元？

表格 1：MATH 训练集中与测试集相似而被过滤的样本示例。

实验结论

基础模型评估

在少样本思维链（few-shot CoT）设置下，Qwen2.5-Math 的基础模型表现出色。

不同规模模型在MATH上的性能比较图 图注：Qwen2.5-Math-1.5/7/72B-Instruct 在 MATH 数据集上使用 CoT 的性能，与其他同尺寸模型对比。

指令微调模型评估

Qwen2.5-Math-Instruct 在英语和中文数学基准上均取得了 SOTA 性能。

英语基准表现 (如 GSM8K, MATH, OlympiadBench 等):

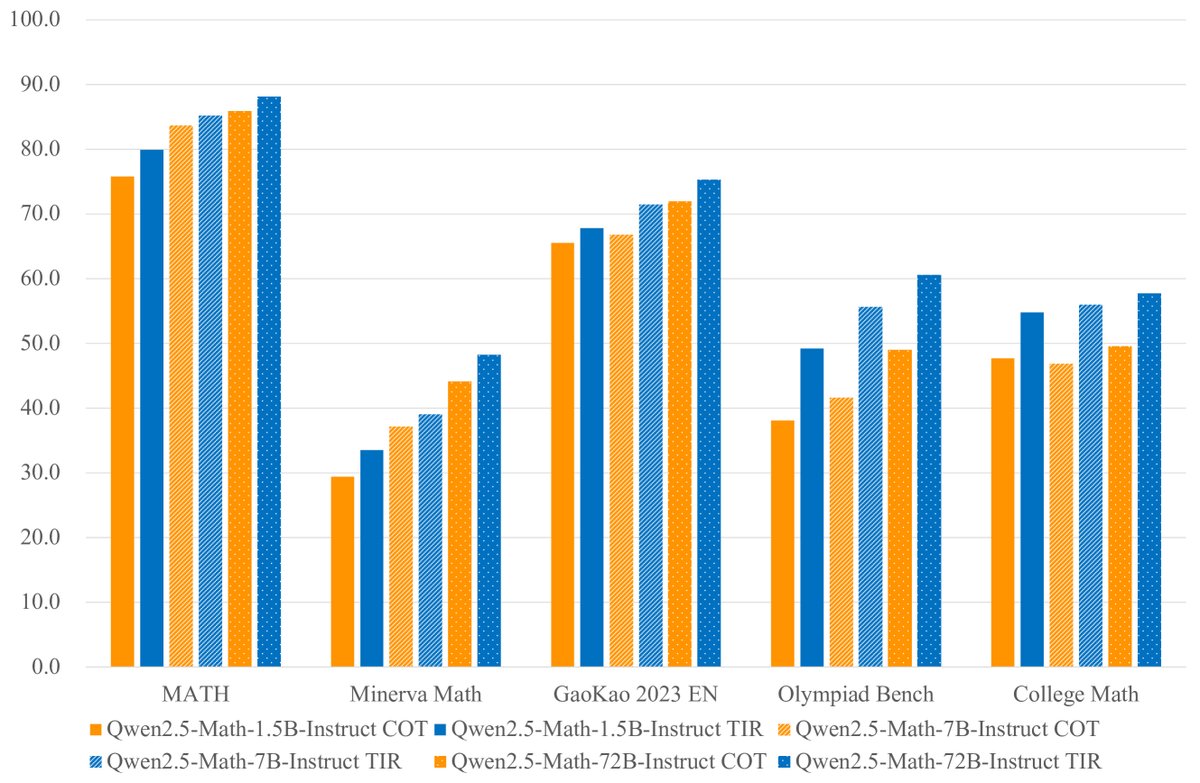TIR与CoT性能对比图 图注：Qwen2.5-Math-Instruct 使用 TIR（蓝色）和 CoT（橙色）的性能对比。可以看出 TIR 带来了显著的性能提升。

中文基准表现 (如 GaoKao, CMATH 等):

高难度竞赛级问题表现: 在 AIME 2024 和 AMC 2023 等极具挑战性的数学竞赛基准上，Qwen2.5-Math-Instruct 相比前代模型表现出显著的性能提升，证明其在解决复杂数学问题上的强大能力。

最终结论：本文通过系统性地应用“自我改进”方法论，结合高质量的 CoT 和 TIR 数据合成，以及“SFT-RM-RL”的先进训练流程，成功打造了 Qwen2.5-Math 这一数学专家模型系列。该系列模型不仅在多项英、中文数学基准上树立了新的 SOTA，还证明了通过改进数据和训练策略是提升模型能力的一条与扩大模型规模同样重要、甚至更高效的路径。