Re4: Scientific Computing Agent with Rewriting, Resolution, Review and Revision

• ArXiv URL: http://arxiv.org/abs/2508.20729v1

• 作者: Lei Zhang; Ao Cheng; Guowei He

• 发布机构: Chinese Academy of Sciences; University of Chinese Academy of Sciences

---

TL;DR

本文提出了一个名为 Re⁴ 的科学计算智能体 (Agent) 框架，它通过“重写-解决-审查-修订” (Rewriting-Resolution-Review-Revision) 的逻辑链，利用多个大型语言模型 (LLM) 协同工作，显著提升了根据自然语言描述自主生成代码的可靠性和准确性。

关键定义

本文的核心是 Re⁴ 框架，其关键概念包括：

• Re⁴ 逻辑链: 指代“重写-解决-审查-修订” (Rewriting-Resolution-Review-Revision) 的四步闭环流程。这是智能体解决科学计算问题的核心思想，模拟了人类专家“草稿-反思-修正”的迭代过程。
• 顾问 (Consultant): 框架中的一个模块，由一个 LLM 驱动。它负责“重写 (Rewriting)”阶段，通过引入领域知识来扩充和细化原始问题描述，为后续的解决方案设计提供丰富的上下文和算法策略建议。
• 程序员 (Programmer): 框架中的核心执行模块，由另一个 LLM 驱动。它负责“解决 (Resolution)”阶段，根据顾问模块增强后的任务文本生成并执行代码。同时，它接收审查员的反馈以进行“修订 (Revision)”。
• 审查员 (Reviewer): 框架中独立的第三方评估模块，由一个独立的 LLM 驱动。它负责“审查 (Review)”阶段，通过评估程序员生成的代码、算法和运行时输出（包括错误、警告和结果）来提供详细的反馈，从而驱动智能体的自我调试和自我改进。

相关工作

当前，使用大型语言模型 (LLM) 进行科学计算面临两大核心挑战：

1. 自主性问题：如何让 LLM 在没有人类干预的情况下，为特定问题自主选择和实现合适的数值方法。
2. 可靠性问题：如何确保 LLM 将模糊的自然语言描述准确地转化为无错误的、可执行的代码。

尽管最新的推理型 LLM 在科学计算任务上表现出潜力，但它们生成的代码仍然频繁出现错误，尤其在处理具有挑战性的问题（如病态线性系统）时，其成功率很低。此外，它们在选择数值方法时存在随机性强、输出不稳定和“推理幻觉”等问题，严重影响了结果的可靠性。

现有的 LLM 智能体框架，如 CodePDE、PINNsAgent 等，虽然引入了迭代调试或领域知识，但往往是单模型架构，并且缺少一个结构化的、能与代码实际运行结果深度交互的审查和修订机制。

本文旨在解决上述自主性和可靠性瓶颈，提出一个多智能体协作框架，以实现从自然语言描述到高质量、可执行代码的端到端自动化生成。

	推理	扩展	调试	优化	审查	单/多LLM
非推理型 LLM	✗	✗	✗	✗	✗	单一
推理型 LLM	✓	✗	✗	✗	✗	单一
CodePDE Agent	✓	✗	✓ (基于后验误差)	✗	✗	单一
PINNsAgent	✓	✗	✓	✓	✗	单一
Madaan’s Agent	✗	✗	✗	✓	✗	单一
本文智能体	✓	✓	✓	✓	✓	多个

表1: 现有用于科学计算的 LLM 智能体框架与本文所提出框架的比较

本文方法

本文构建了一个名为 Re⁴ 的新型科学计算智能体框架，其核心是一个由三个协同模块组成的“重写-解决-审查-修订”逻辑链。

图1: 智能体框架示意图

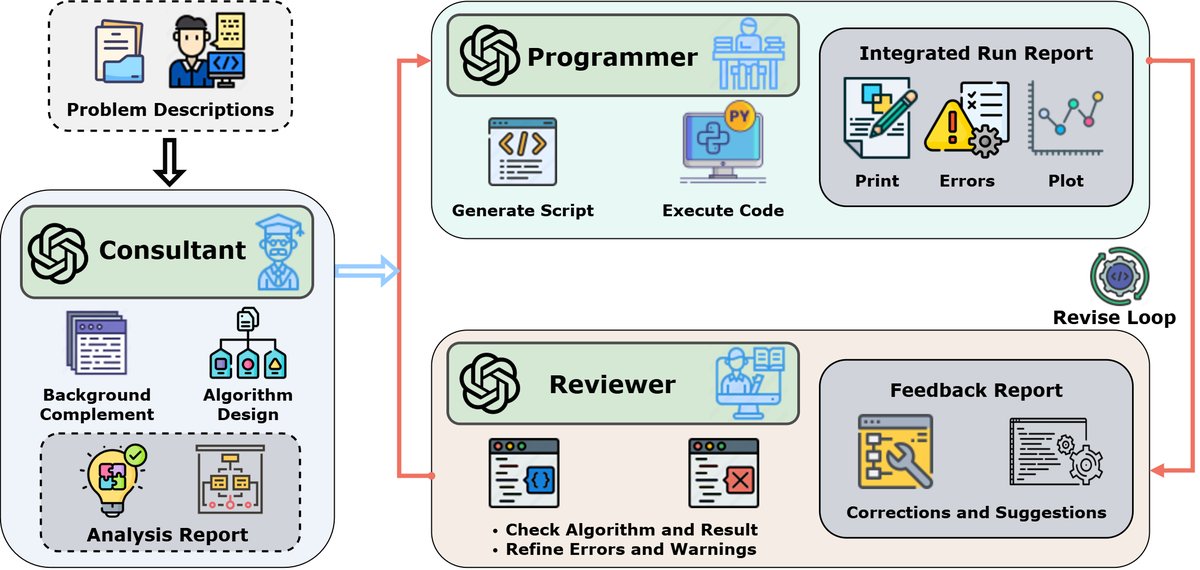
该框架包含三个由 LLM 驱动的核心模块：

1. 顾问 (Consultant) 模块

• 职责: 负责重写 (Rewriting) 阶段。
• 工作流程: 接收用户输入的自然语言问题描述（例如，一个偏微分方程）。该模块的 LLM 会利用其内部知识，对问题背景进行详细阐述，扩展上下文，并提出多种可行的算法策略。
• 输出: 一份增强后的任务报告，通过文本扩充加深了对特定科学计算任务的理解，为程序员模块提供了高质量的输入。

2. 程序员 (Programmer) 模块

• 职责: 负责解决 (Resolution) 和修订 (Revision) 阶段。
• 工作流程:
  • 在初始阶段，它接收顾问模块的增强文本，选择算法，生成 Python 代码，并在终端中执行。
  • 在修订循环中，它接收来自审查员模块的反馈，并据此修改和完善代码。
• 输出: 可执行的 Python 代码及在编译器中的运行结果。

3. 审查员 (Reviewer) 模块

• 职责: 负责审查 (Review) 阶段，是实现自我优化的关键。
• 工作流程: 该模块由一个独立于程序员模块的 LLM 驱动，以确保评估的客观性。它接收三部分输入：顾问的增强文本、程序员的代码、以及代码的运行时输出（包括警告、错误和计算结果）。
• 输出: 一份全面的评估报告，主要包含：
  • 对程序员算法实现的综合评价。
  • 如果代码存在 bug，提供具体的调试建议。
  • 为提升性能，提出关于算法选择、参数设置和代码实现的优化建议。

创新点

1. 多智能体协作框架: 首次在科学计算领域引入了“顾问-程序员-审查员”三角色协作模式。这种架构允许不同角色的模块由不同的 LLM（如 GPT, Gemini, DeepSeek）担任，克服了单一模型固有的推理局限和“幻觉”问题。
2. 闭环反馈与自我优化: 通过“程序员”和“审查员”之间的反馈循环，智能体能够与真实的代码运行结果进行交互。这种基于实际执行反馈的自我调试和自我优化机制，是提升代码质量和解决问题可靠性的核心。
3. 知识增强的重写阶段: 在解决问题之初，顾问模块通过引入领域知识来丰富问题描述，这种“重写”步骤确保智能体在设计算法前能更深刻地理解问题本质，从而做出更优的策略选择。

实验结论

本文在三类具有代表性的科学计算任务上对 Re⁴ 框架进行了全面评估：偏微分方程 (PDE) 基准测试、病态希尔伯特 (Hilbert) 线性系统求解、以及基于量纲分析的数据驱动物理分析。

评估指标:

• 代码执行成功率: 生成无 bug 且能返回非 NaN 解的代码的百分比。
• 求解成功率: 在特定任务中，达到预设标准的百分比（如误差低于阈值或成功识别物理规律）。
• 准确度: 计算结果与参考解之间的 $L^2$ 或 $L^\infty$ 相对误差。

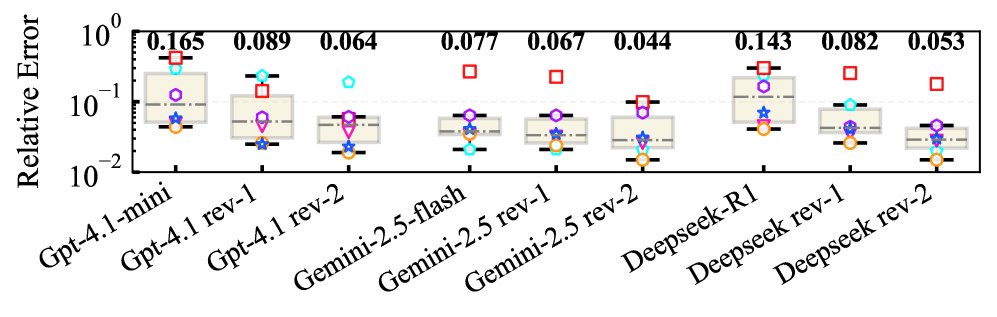
1. 偏微分方程 (PDE) 基准测试

Re⁴ 框架在求解多种 PDE（如 Burgers 方程、Navier-Stokes 方程等）时表现出色。

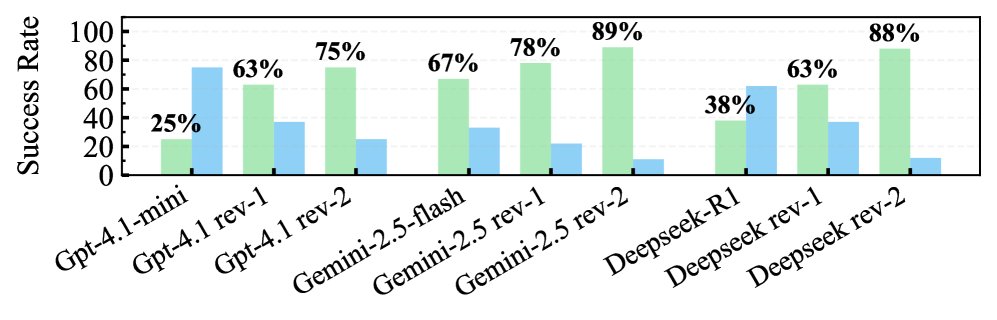
• 可靠性提升: 审查机制显著提升了代码的执行成功率。例如，在使用 DeepSeek R1 作为“程序员”时，成功率从 59% 提高到 82%；使用 ChatGPT 4.1-mini 时，从 66% 提高到 87%。

图2: 在 PDEbench 所有方程中，程序员所用数值算法的总体平均执行成功率

• 精度提升: 经过审查员的指导，所有测试模型的求解精度（平均 $L^2$ 相对误差）均得到改善，误差分布也更加集中。

Programmer	Gpt-4.1-mini			Gemini-2.5-flash			Deepseek-R1
	ans-0	rev-1	rev-2	ans-0	rev-1	rev-2	ans-0	rev-1	rev-2
Burgers	5.8e-02	2.5e-02	2.3e-02	4.1e-02	3.5e-02	3.1e-02	7.0e-02	4.1e-02	3.0e-02
Sod Shock	1.3e-01	6.0e-02	6.1e-02	6.4e-02	6.4e-02	7.0e-02	1.7e-01	4.4e-02	4.6e-02
Poisson	4.4e-02	2.6e-02	1.9e-02	3.5e-02	2.4e-02	1.5e-02	4.1e-02	2.6e-02	1.5e-02
Helmholtz	4.9e-02	4.5e-02	3.7e-02	3.4e-02	3.2e-02	2.6e-02	4.5e-02	3.5e-02	2.8e-02
Lid-Driven	4.2e-01	1.4e-01	5.7e-02	2.7e-01	2.3e-01	9.9e-02	3.0e-01	2.6e-01	1.8e-01
Unsteady NS	2.9e-01	2.3e-01	1.9e-01	2.1e-02	2.1e-02	2.1e-02	2.4e-01	9.0e-02	2.0e-02

表3: PDEbench 中所有案例的平均相对 $L^2$ 误差总结

图3: PDEbench 中所有方程的平均 $L^2$ 相对误差箱线图

2. 希尔伯特 (Hilbert) 线性系统

对于这个经典的病态问题，初始的 LLM 模型往往无法给出有效解。

• 求解能力质变: 审查机制使得智能体能学会采用更高级的数值方法（如正则化技术或共轭梯度法）来应对病态矩阵。GPT-4.1-mini 的求解成功率（误差低于 $10^{-2}$）从 0% 跃升至 57%，Deepseek-R1 从 11% 提升至 46%。

图7: 程序员提供的可执行代码在三种不同完成状态下的比例分布

3. 数据驱动的物理分析

任务是根据实验数据，通过量纲分析发现主导物理现象的无量纲数。

• 物理规律发现: 在审查员的指导下，智能体能够更好地执行维度一致性检查，修正搜索算法，从而更准确地识别出关键的无量纲数（Keyhole 数, Ke）。其发现正确物理规律的成功率最高提升了 50%。

图9: 程序员搜索算法识别主导无量纲数 Ke 的成功率

总结

实验结果充分证明，Re⁴ 框架通过其独特的“重写-解决-审查-修订”逻辑链和多智能体协作机制，在可靠性、准确性和问题解决能力上均显著优于单一 LLM 模型。它为实现科学计算任务的自动化建立了一个高可靠性的范式，并展示了其在不同领域的通用性和巨大潜力。