Reinforcement learning

引言

强化学习 (Reinforcement Learning, RL)，在深度神经网络的推动下，已在多个学科取得重大突破，例如在计算机游戏、棋类对弈、机器人技术以及矩阵乘法和排序等高效算法开发中都展现了卓越能力。

在天文学领域，强化学习也开始崭露头角，其应用包括望远镜的自动化控制（如自适应光学和反射面控制）、观测调度以及射电天文数据处理流水线中的超参数调优。考虑到现代天文学可以被视为从望远镜到科学家的信息流，强化学习有望在辅助和优化这一流程的众多环节中发挥更大作用，这也是本文撰写的动机。

机器学习 (Machine Learning, ML) 主要包含三种范式：

  1. 监督学习 (Supervised learning)：为机器提供输入和对应的期望输出，让其学习任务。
  2. 无监督学习 (Unsupervised learning)：只为机器提供输入数据。
  3. 强化学习 (Reinforcement learning)：机器通过与外部环境的反复试错交互，并根据获得的反馈来学习执行任务。与前两者不同，强化学习具有显著的时间维度，任务被视为一系列连续的动作，而非单步决策。

本文旨在对现代深度强化学习进行综述，并侧重其在天文学领域的应用，为新用户提供一个简洁而全面的入门指南，以便他们能快速将相关技术应用于自己的工作中。

强化学习理论

本节简要概述强化学习的理论基础，主要基于机器学习的视角，同时融合了动态规划、控制论甚至神经科学等多个学科的交叉思想。

状态、动作与奖励

强化学习的核心框架涉及一个智能体 (agent) 与其环境 (environment) 的交互，如图1所示。智能体为了达成特定目标，根据从环境接收到的观测 (observations) 来执行动作 (action)。环境接收动作后状态发生改变，并向智能体反馈一个奖励 (reward)，该奖励是对动作质量的数值化评价。

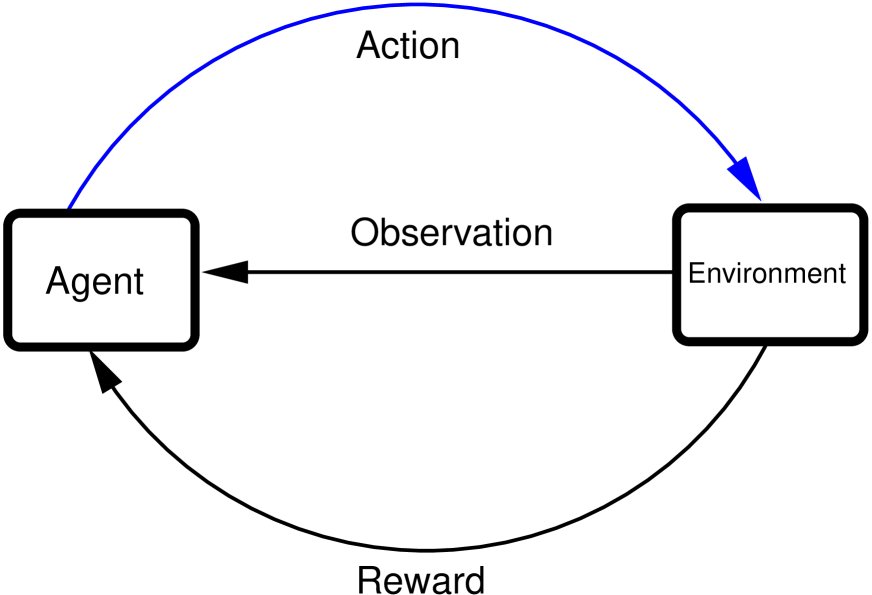
智能体与环境的交互

图1: 智能体与环境的交互。智能体接收观测、执行动作并获得相应的奖励。

这个交互过程可以被数学化地描述：

下表列出了一些强化学习应用的例子：

问题 目标 状态 动作
国际象棋 赢得比赛 棋盘上所有棋子的位置 选择并移动一个棋子
双足机器人行走 行走 腿部关节的位置、速度等 对各腿部关节施加力矩
自动驾驶汽车 到达目的地 自身及其他车辆的位置、速度、加速度；油量、路况、路标、行人等 施加力以实现加速、刹车、转向等

马尔可夫决策过程

智能体与环境的交互是一个持续循环的过程，在时间步 $t$，智能体接收状态 $s_t$ 和奖励 $r_t$，并输出动作 $a_t$；环境执行 $a_t$ 后，转移到新状态 $s_{t+1}$，并给出新的奖励。这个过程通常是分幕式 (episodic) 的，即在一系列步骤后会达到一个终止状态（成功或失败）。

这个过程可以用马尔可夫决策过程 (Markov Decision Process, MDP) 来形式化，它由一个四元组 $(\mathcal{S}, \mathcal{A}, \mathcal{R}, \mathcal{P})$ 定义。其中 $\mathcal{P}$ 是状态转移概率。马尔可夫特性 (Markov property) 指的是，在时间步 $t$ 的状态转移概率仅依赖于当前状态 $s_t$ 和采取的动作 $a_t$，即 $p(s_{t+1} \mid s_t, a_t)$。

智能体的学习目标不是最大化即时奖励，而是最大化未来奖励的折扣累积和 (discounted cumulative reward)。这引入了折扣因子 (discount factor) $\gamma$ ($0 < \gamma < 1$)，它平衡了短期奖励和长期奖励的重要性，并确保在无限时间范围内的奖励总和收敛。

Q函数、价值函数与策略

为了解决RL问题，我们引入了几个核心概念，并通过一个简单的迷宫示例（图2）进行说明。智能体的目标是从任意空格移动到右上角的目标位置。

迷宫环境

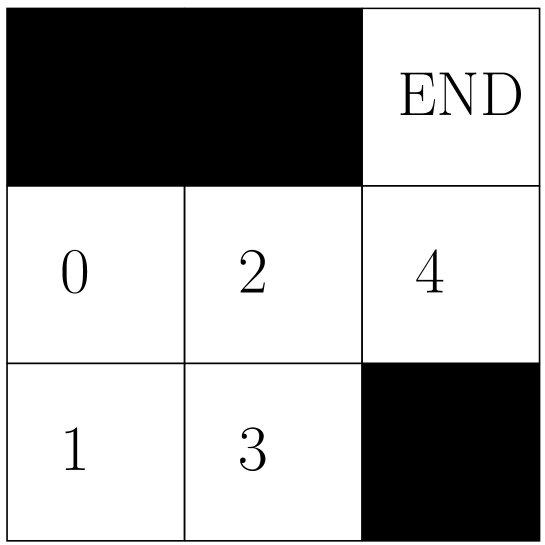
图2: 迷宫环境，包含5个有效状态（0-4）和4种动作（上、下、左、右）。

为了实现目标，我们定义了奖励表（表2），并引入Q表来评估每个状态-动作对的“质量”。

表2: 迷宫环境的奖励表 $R[s, a]$

状态 $\rightarrow$ $\leftarrow$ $\uparrow$ $\downarrow$
0 -1 $-\infty$ $-\infty$ -1
1 -1 $-\infty$ -1 $-\infty$
2 -1 -1 $-\infty$ -1
3 $-\infty$ -1 -1 $-\infty$
4 $-\infty$ -1 100 $-\infty$

通过算法1（一种简化的Q学习）反复迭代更新Q表 $Q[s,a]$，最终可以得到一个收敛的Q表（表3），它指导智能体在任何状态下选择最优动作。

表3: 迷宫环境收敛后的Q表 ($\gamma=0.9$)

状态 $\rightarrow$ $\leftarrow$ $\uparrow$ $\downarrow$
0 79.1 0 0 62.171
1 70.19 0 70.19 0
2 89 70.19 0 70.19
3 0 62.171 79.1 0
4 0 0 100 0

对于高维或连续空间问题，表格法不再适用，需要使用函数逼近器（通常是深度神经网络）来表示以下概念：

  1. 策略 (Policy): 从状态到动作的映射。确定性策略 $\pi(s)$ 直接输出动作 $a$，而随机性策略 $\pi(a \mid s)$ 输出给定状态下动作的概率分布。
  2. Q函数 (Q-function): 状态-动作价值函数 $Q(s,a)$，衡量在状态 $s$ 下采取动作 $a$ 的预期累积奖励。
  3. 价值函数 (Value function): 状态价值函数 $V(s)$，衡量处在状态 $s$ 的好坏程度，即从该状态开始遵循某一策略所能获得的预期累积奖励。

这些函数之间的关系由贝尔曼方程 (Bellman equation) 定义，它是RL问题最优性的基础：

\[Q(s,a) = r(s,a)+\gamma\underset{a'=\pi(s')}{\mathrm{max}}Q(s',a')\]

解决RL问题，本质上就是学习到最优的策略函数 $\pi(s)$、Q函数 $Q(s,a)$ 或价值函数 $V(s)$。深度神经网络因其强大的表示能力和现成的梯度下降优化框架，成为表示这些函数的理想选择。

深度强化学习算法

本节重点讨论无模型 (model-free) 的深度强化学习算法。在训练智能体时，通常面临以下挑战：

经验回放

为了解决数据不足和训练不稳定性问题，经验回放 (Experience replay) 技术被广泛采用。该方法将智能体与环境交互的样本，即元组 $(s, a, r, s’)$，存储在一个称为回放缓冲区 (replay buffer) $\mathcal{D}$ 的大容量存储中。在训练时，从 $\mathcal{D}$ 中随机采样一个小批量 (mini-batch) 数据进行学习。这打破了数据之间的时间相关性，提高了数据利用率和训练稳定性。这种使用历史数据（可能由旧策略产生）的训练方式属于离策略 (off-policy) 算法。算法2展示了使用经验回放的通用训练流程。

分类体系：基于动作空间的算法

本文将深度强化学习算法依据动作空间 (action space) 的类型进行分类，主要分为离散动作空间算法和连续动作空间算法。

离散动作空间强化学习

当动作空间 $\mathcal{A}$ 是离散且有限时，主要使用基于Q学习的算法。

Q学习 (Q-learning) 的更新规则是：

\[Q(s,a) \leftarrow Q(s,a) + \mu \left( r(s,a) + \gamma \underset{a'}{\mathrm{max}} Q(s',a') - Q(s,a) \right)\]

其中 $\mu$ 是学习率。

深度Q网络 (Deep Q-Network, DQN) 使用深度神经网络 $Q_\theta(s,a)$ 来近似Q函数。为了解决训练不稳定的问题，DQN引入了目标网络 (target network) $Q_{\theta’}(s,a)$。训练时，Q网络 $Q_\theta$ 的参数 $\theta$ 通过最小化以下损失函数进行更新，而目标网络的参数 $\theta’$ 则保持冻结，仅定期从 $Q_\theta$ 复制参数（$\theta’ \leftarrow \theta$）。

\[J(\theta) = \ \mid r(s,a) + \gamma \underset{a'}{\mathrm{max}} Q_{\theta'}(s',a') - Q_{\theta}(s,a) \ \mid ^{2}\]

双重Q学习 (Double Q-learning) 进一步解决了Q学习中普遍存在的Q值过高估计问题。它使用两个独立的Q网络（$Q_1$ 和 $Q_2$），在计算目标Q值时，一个网络用于选择动作，另一个网络用于评估该动作的价值，从而解耦选择和评估过程，减少过高估计。

连续动作空间强化学习

当动作空间是连续时，无法通过遍历所有动作来找到最大Q值，因此需要采用不同的方法。行动者-评论家 (Actor-Critic) 方法是解决此类问题的标准框架。它将智能体分解为两部分（如图3所示）：

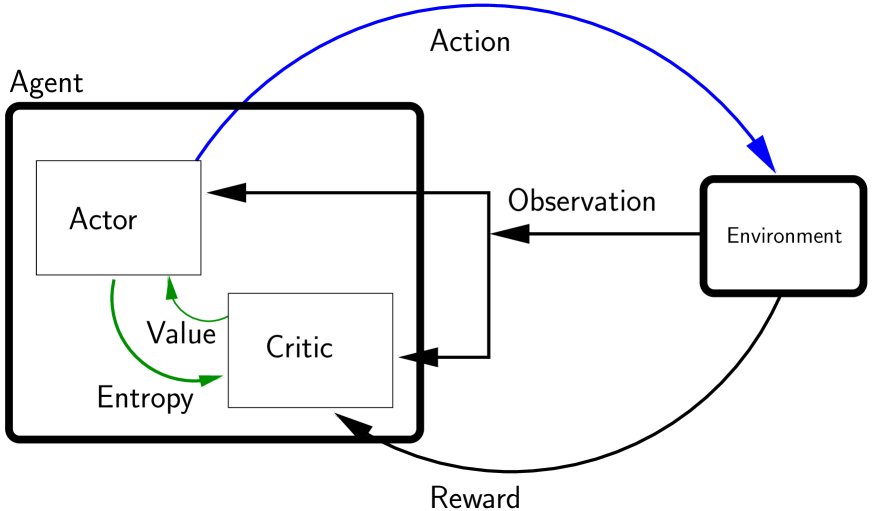
行动者-评论家架构

图3: 由行动者和评论家组成的强化学习智能体。

3.3.1 DDPG (Deep Deterministic Policy Gradient)

DDPG是一种用于连续动作空间的离策略行动者-评论家算法。

\[J(\theta) = \ \mid r(s,a) + \gamma Q_{\theta'} \left( s', \pi_{\phi'}(s') \right) - Q_{\theta}(s,a) \ \mid ^{2}\] \[J(\phi) = -Q_{\theta}\left(s, \pi_{\phi}(s)\right)\]

目标网络参数则通过Polyak平均 (Polyak averaging) 进行软更新，即缓慢地跟踪主网络的参数。

3.3.2 TD3 (Twin Delayed DDPG)

TD3是DDPG的改进版，旨在解决其Q值过高估计和训练不稳定的问题，主要包含三项关键技术：

  1. 双评论家网络 (Twin Critics)：使用两个独立的Q网络 ($Q_{\theta_1}, Q_{\theta_2}$)，在计算目标Q值时，取两者中的较小值。这有效抑制了Q值的过高估计。
\[J(\theta_i) = \ \mid r(s,a) + \gamma \underset{j=[1,2]}{\mathrm{min}} Q_{\theta'_{j}}\left(s',a'\right) - Q_{\theta_i}(s,a)\ \mid ^{2}\]
  1. 延迟策略更新 (Delayed Policy Updates)：行动者（策略网络）的更新频率低于评论家（Q网络），例如每更新两次评论家才更新一次行动者。这使得Q值的估计更稳定后，再指导策略的改进。
  2. 目标策略平滑 (Target Policy Smoothing)：在计算目标Q值时，对目标行动者网络输出的动作加入少量噪声并进行裁剪，使Q函数对动作的微小变化不那么敏感，从而平滑价值函数的估计。

3.3.3 SAC (Soft Actor-Critic)

SAC是一种基于最大熵强化学习 (maximum entropy reinforcement learning) 框架的离策略行动者-评论家算法。与DDPG/TD3不同，SAC使用随机性策略 (stochastic policy) $\pi(a \mid s)$。

\[J(\theta_i) = \ \mid r(s,a) + \gamma \left( \underset{j=[1,2]}{\mathrm{min}} Q_{\theta'_{j}}(s',a') - \alpha \log\pi_\phi(a' \mid s') \right) - Q_{\theta_i}(s,a)\ \mid ^2\]

其中，$\alpha$ 是一个权衡奖励和熵的温度系数，可以手动调节或自动学习。这种内在的探索机制使得SAC在样本效率和鲁棒性方面通常表现优异。