Reinforcement Learning Fine-Tuning Enhances Activation Intensity and Diversity in the Internal Circuitry of LLMs

TL;DR

本文通过边缘归因修补（EAP）方法分析发现，在线强化学习（RL）微调能系统性地增强大语言模型（LLM）内部回路的激活强度和模式多样性，从而提升模型能力，而直接偏好优化（DPO）则不具备此效应。

关键定义

本文沿用了现有定义，并提出了几个关键分析指标，对理解其核心贡献至关重要：

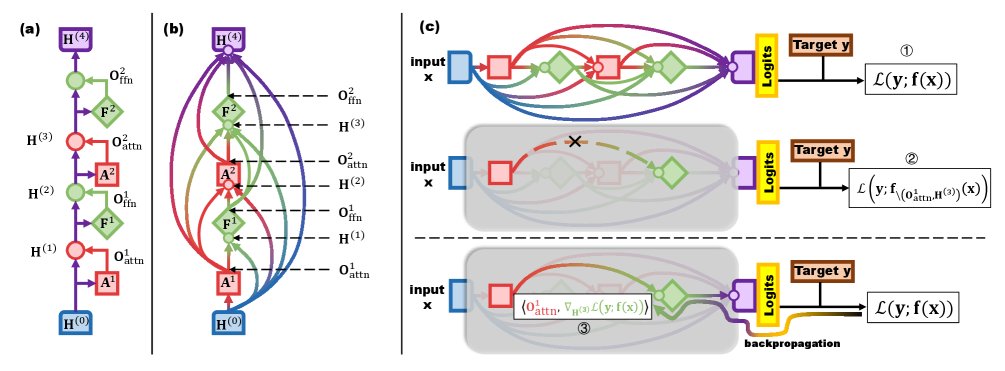
  1. Transformer的图视角 (Graph View of Transformer)：本文将 Transformer 模型抽象为一个有向无环图（DAG）。图中的节点对应于模型中的计算子模块（如多头注意力块和前馈网络块），而边则代表了通过残差连接（residual connections）实现的信息流路径。这个视角是进行内部回路分析的基础。

  2. 边缘归因修补 (Edge Attribution Patching, EAP)：一种用于估计模型内部信息路径重要性的高效方法。与通过“切断”某条边并计算损失变化的“烧蚀”方法不同，EAP 通过一次前向和一次反向传播，利用损失函数对隐藏状态的梯度与该路径上的激活输出的内积，来近似计算每条边的重要性。其计算公式为 $I_{\text{EAP}} \approx -\left\langle\nabla_{\mathbf{H}}\mathcal{L}, \mathbf{O}\right\rangle$，大大提升了分析大规模模型内部回路的可行性。

  3. 激活强度 (Activation Intensity)：用于量化模型内部通路激活程度的指标。它通过计算所有样本中所有边权重（即EAP计算出的重要性得分）的绝对值的平均值来衡量。更高的激活强度意味着更多的内部路径被激活，且信号传递更强。

  4. 信息复杂度 (Information Complexity)：基于香农熵的指标，用于衡量模型内部激活模式的多样性和不可预测性。它通过计算所有边权重绝对值构成的整体分布的熵来度量。熵值越高，表明激活模式越多样化、越不集中。

  5. 分布峰度 (Distribution Kurtosis)：用于衡量每个样本的边权重分布形态的指标。通过计算每个样本内边权重分布的峰度，并求所有样本的平均值，来评估激活模式的集中程度。峰度降低通常意味着分布更平坦，激活模式更分散、更多样。

相关工作

当前对大语言模型（LLM）的研究存在两条平行的主线。第一条主线关注模型后训练（post-training）方法，大量实证研究表明，基于强化学习（Reinforcement Learning, RL）的微调（如PPO、GRPO）相比单独使用监督微调（Supervised Fine-Tuning, SFT）能够更显著地提升模型在推理、编码等复杂任务上的能力。然而，这些研究大多停留在外部行为的评估上，对于RL为何能带来这些性能提升的内部机制缺乏深入探索。

第二条主线是LLM的可解释性研究，旨在探究模型内部的工作机理。研究者们发展了如自动电路发现（ACDC）、边缘归因修补（EAP）等方法，通过分析神经元、注意力头和信息通路来理解模型的决策过程。但这些分析往往针对给定的、已经训练好的模型，并未将其内部机制的变化与获得该模型的RL训练过程联系起来。

因此，当前研究存在一个明显的断层：一方面我们知道RL能提升模型表现，另一方面我们有工具分析模型内部，但缺乏将两者结合的研究。本文旨在解决这一具体问题：系统性地揭示RL微调是如何通过改变LLM的内部信息流（或称“内部回路”）来提升其能力的。

本文方法

本文提出了一套系统的分析框架，以探究强化学习微调对LLM内部回路的影响。该方法的核心是适配并应用了边缘归因修补（EAP）框架。

## 方法框架

该分析框架主要包含以下几个步骤：

  1. 模型图化表示：首先，将Transformer模型视为一个有向无环图（DAG）。模型中的每个注意力（Attention）子模块和前馈网络（FFN）子模块被看作图中的节点。由于残差连接的存在，任何一个子模块的输入都是其前面所有子模块输出的总和，这些信息流动路径构成了图的边。

  2. 边重要性估计：为了量化每条信息路径（边）的重要性，本文采用了高效的EAP方法。其基本思想是，一条边的重要性可以通过移除该边（即将其贡献清零）导致的损失变化来衡量。EAP通过一阶泰勒展开近似这个过程，将边的重要性 $I_{\text{EAP}}$ 定义为损失 $\mathcal{L}$ 对该边终点隐藏状态 $\mathbf{H}$ 的梯度与该边源头激活输出 $\mathbf{O}$ 的内积：

    \[I_{\text{EAP}}(\mathbf{O},\mathbf{H}) \approx -\left\langle\nabla_{\mathbf{H}}\mathcal{L}(\mathbf{y};\mathbf{f}(\mathbf{x})), \mathbf{O}\right\rangle\]

    这种基于梯度的方法仅需一次前向和一次反向传播即可计算所有边的重要性，相比需要多次前向传播的烧蚀方法（如ACDC）计算效率极高。

  3. 受控的样本分析：为保证比较的公平性，本文设计了一套严格的样本筛选和处理流程。

    • 问题筛选：仅选择SFT和RL模型都能正确回答的问题。
    • 长度控制：过滤掉答案过长或过短的样本，并确保同一问题下，SFT和RL模型生成的答案长度相近，以消除长度偏差。
    • 截断与损失计算：对筛选后的生成序列进行部分截断，并使用模型对自身截断后输出的交叉熵（自熵）作为损失函数 $\mathcal{L}$ 来计算梯度，从而进行EAP分析。

## 创新点

本文的核心创新在于系统性地应用EAP来对比分析LLM在RL微调前后的内部回路变化，从而架起了RL性能提升（外部表现）与其内部机理变化（内部解释）之间的桥梁。它首次揭示了不同RL算法（在线RL vs. DPO）对模型内部信息流产生的系统性差异。

## 优点

该方法的主要优点是高效和通用。通过采用基于梯度的EAP，使得对拥有数十亿参数的大模型进行细粒度的回路分析在计算上成为可能。此外，该分析框架不依赖于特定的模型架构或任务，可广泛应用于研究不同后训练方法对各类LLM内部机理的影响。

实验结论

本文通过对四组不同模型家族（Deepseek-Math、Mistral、Distilled-Qwen、Qwen2.5）在数学推理任务上的对比实验，系统地验证了在线强化学习微调对LLM内部回路的系统性影响。

Schematic of a two-layer simplified LLM. (a) Residual perspective, (b) graph perspective, and (c) edge importance estimation: above the dashed line, ACDC-style methods measure the loss change after edge ablation ($②-①$); below, EAP-style methods approximate this via backpropagated gradients ($-③\approx②-①$).

## 关键实验结果

实验通过三个核心指标——激活强度、信息复杂度和分布峰度——量化了RL微调前后的内部变化。

数据集 指标 SFT vs GRPO SFT vs PPO SFT vs GRPO SFT vs DPO
MATH 激活强度 $\uparrow$ 显著增加 显著增加 显著增加 减弱或不一致
  信息复杂度 $\uparrow$ 显著增加 显著增加 显著增加 不一致
  分布峰度 $\downarrow$ 显著下降 显著下降 显著下降 不一致
College Math 激活强度 $\uparrow$ 显著增加 显著增加 显著增加 不一致
  信息复杂度 $\uparrow$ 显著增加 显著增加 显著增加 不一致
  分布峰度 $\downarrow$ 显著下降 显著下降 显著下降 不一致
GSM8K 激活强度 $\uparrow$ 显著增加 显著增加 显著增加 不一致
  信息复杂度 $\uparrow$ 显著增加 显著增加 显著增加 不一致
  分布峰度 $\downarrow$ 显著下降 显著下降 显著下降 不一致

表格总结自原文Table 1，展示了在PPO、GRPO和DPO三种RL算法下，相比SFT基座模型，三个关键指标的普遍变化趋势。蓝色表示符合预期的变化，绿色表示不符合。

  1. 在线RL增强内部回路：对于采用在线RL算法（PPO和GRPO）微调的模型，实验观察到两个一致且稳健的效应：
    • 激活强度提升：RL微调后，模型内部连接的平均激活强度普遍增加。这表明更多的信息通路被激活，并且信号在这些通路中的传递变得更强。
    • 激活模式多样化：RL微调后，信息复杂度（熵）增加，而分布峰度下降。这说明边的激活权重分布变得更平坦、更多样化，信息流不再集中于少数几个路径，而是以更灵活、更多样的方式在模型内部传递。
  2. DPO的独特性：与在线RL不同，使用直接偏好优化（DPO）进行微调的模型（Qwen2.5）并未表现出上述一致的变化趋势。其内部激活强度和多样性的变化非常微弱或不一致。

Relative change in edge activation strength after RL fine-tuning for the Mistral model on the MATH dataset with $\alpha=0.5$. 上图展示了Mistral模型经过PPO微调后，内部边激活强度的相对变化，证实了RL微调能系统性地增强内部信号传播。

Comparison before and after RL fine-tuning: (a) diversity of activation patterns across inference samples, (b) entropy of output edge patterns per node. 上图(a)和(b)分别从样本间和节点输出两个维度展示了RL微调后激活模式多样性的提升。

## 结论

本文的最终结论是：

  1. 在线RL微调通过重塑LLM的内部信息流来提升其泛化能力。具体而言，它使得信息流变得更冗余（激活强度更高）和更灵活（激活模式更多样），这可能是其在复杂任务上超越SFT的根本原因。

  2. DPO与在线RL在机制上存在本质区别。DPO依赖于一个固定的、离线的偏好数据集进行训练，类似于SFT，无法在训练中探索和激活更广泛的神经通路。而PPO、GRPO等在线RL算法通过与持续演进的策略进行交互，能够探索更广阔的输出空间，从而更深刻地重塑模型内部结构。这一发现为解释不同对齐算法间的性能差异提供了新的机理视角。