Relative-Based Scaling Law for Neural Language Models

TL;DR

本文提出了一种基于相对排序的新指标——相对概率（RBP），并据此建立了相对标度律（Relative-Based Scaling Law），该定律揭示了模型将正确答案排在靠前位置的能力如何随模型规模的增大而遵循幂律提升，为理解大语言模型提供了补充交叉熵的全新视角。

关键定义

本文提出或沿用了以下关键概念：

  1. 相对概率 (Relative-Based Probability, RBP)：本文提出的核心新指标，用于衡量模型将真实标签Token排在预测结果前列的能力。具体而言，$\text{RBP}_{k}$ 定义为真实标签Token的预测排名 \(R\) 小于等于 \(k\) 的概率，即 $\text{RBP}_{k}=\Pr(R\leq k)$。它关注的是预测的相对顺序，而非绝对概率值。

  2. 相对标度律 (Relative-Based Scaling Law)：本文发现并提出的新标度律。该定律指出，当 \(k\) 远小于词汇表大小时，\(RBP\) 指标与模型非嵌入参数规模 \(S\) 之间存在一个精确的幂律关系：$-\log\big(\text{RBP}_{k}\big)\ \propto\ S^{-\alpha}$，其中 \(α\) 是一个正常数。

  3. 绝对概率指标 (Absolute-Based Metric)：指现有研究中广泛使用的以交叉熵损失为代表的评估指标。这类指标主要衡量模型为真实标签Token分配的绝对概率值，例如交叉熵 $\mathcal{L}_{\text{CE}}=\mathbb{E}[-\log{\rm p_{A}}(t)]$，其中 \(t\) 是真实标签Token。本文指出这类指标忽略了预测的相对排序信息。

相关工作

当前，神经网络语言模型的标度律（Scaling laws）研究几乎完全依赖于交叉熵（cross-entropy）作为核心评估指标。交叉熵是一种绝对概率指标，它衡量模型赋予正确Token的绝对概率值。这些基于交叉熵的标度律已成功指导了许多大模型的训练，并为理解模型机理提供了重要洞见。

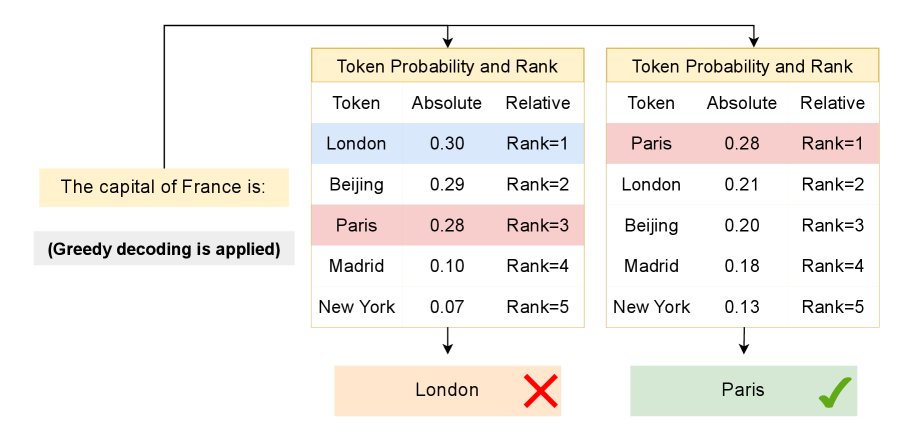
然而，仅依赖交叉熵存在一个关键瓶颈：它无法捕捉预测结果的相对排序信息。如下图所示，即使正确Token的绝对概率相同，其在所有候选Token中的排名可能截然不同。这个排名信息对于贪心解码（greedy decoding）或top-k采样等实际应用至关重要。因此，现有标度律与模型在真实世界中的生成表现之间存在显著差距。

本文旨在解决这一问题，通过引入一个关注相对排序的指标，建立一种新的标度律，以补充现有交叉熵视角的不足，从而更全面地理解模型规模扩展带来的性能变化。

Refer to caption

本文方法

相对概率指标 (RBP)

为了弥补绝对概率指标的不足，本文提出了一种新的相对概率指标，即相对概率（Relative-based Probability, RBP）。

与直接使用模型为真实标签Token \(t\) 分配的概率 ${\rm p_{A}}(t)$ 的交叉熵不同（如下图左所示），RBP关注的是真实标签Token在所有候选者中的排名。

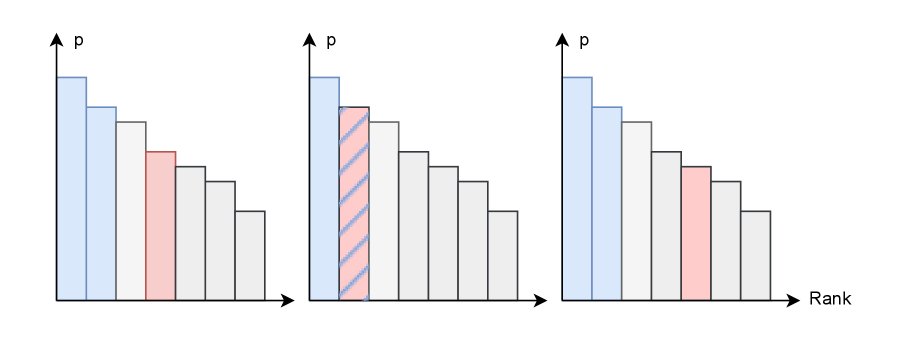
Refer to caption Refer to caption

具体地，真实标签Token的排名 \(R\) 定义为得分不低于它的Token总数：

\[R=\sum_{v\in\mathcal{V}}\mathbf{1}\{{\rm p}(v)\geq p(t)\}\]

其中 \(p(v)\) 是模型对词汇表 \(V\) 中任意Token \(v\) 的预测得分。

基于此，$\text{RBP}_{k}$ 定义为排名 \(R\) 小于或等于 \(k\) 的概率，即真实标签Token出现在模型top-k预测中的概率：

\[\text{RBP}_{k}=\Pr(R\leq k)\]

如上图右所示，$\text{RBP}_{k}$ 通过统计真实标签Token进入top-k预测的频率来计算。该指标与贪心解码（对应 $\text{RBP}_{1}$）和top-k采样（对应 $\text{RBP}_{k}$）等实用策略直接相关，能更准确地反映模型的生成性能。

相对标度律

本文的核心发现是，$\text{RBP}_{k}$ 指标与模型规模 \(S\) 之间存在一个精确的标度律，称为相对标度律。当 \(k\) 远小于词汇表大小时 ($k\ll \mid \mathcal{V} \mid $)，该定律的数学形式为：

\[-\log\text{RBP}_{k}\;\propto\;S^{-\alpha}\quad\big(k\ll \mid \mathcal{V} \mid \big)\]

其中 \(S\) 是模型的非嵌入参数数量，\(α > 0\) 是标度指数。这意味着，随着模型规模的增大，模型将正确答案排入top-k的能力以幂律形式平滑提升。

本文通过在不同 \(k\) 值区间进行实验来验证该定律的有效性。

\(k=1\) Regime

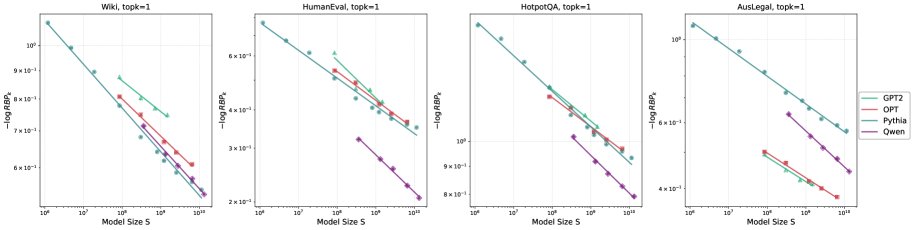
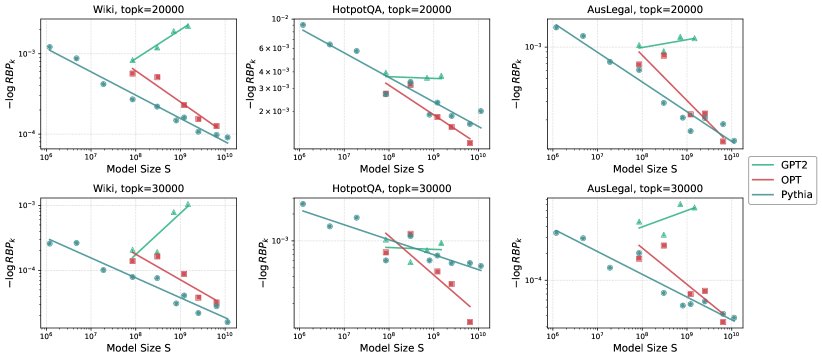
当 \(k=1\) 时，$\text{RBP}_{1}$ 衡量模型将正确Token排在第一位的能力，直接对应贪心解码的成功率。实验结果显示，在所有测试的数据集和模型族上，$-\log(\text{RBP}_{1})$ 与模型规模 \(S\) 在双对数坐标下呈现出清晰的线性关系，拟合优度 $R^2$ 接近0.99，证实了标度律的成立。

Refer to caption

中等\(k\) Regime: \(1 < k <= 100\)

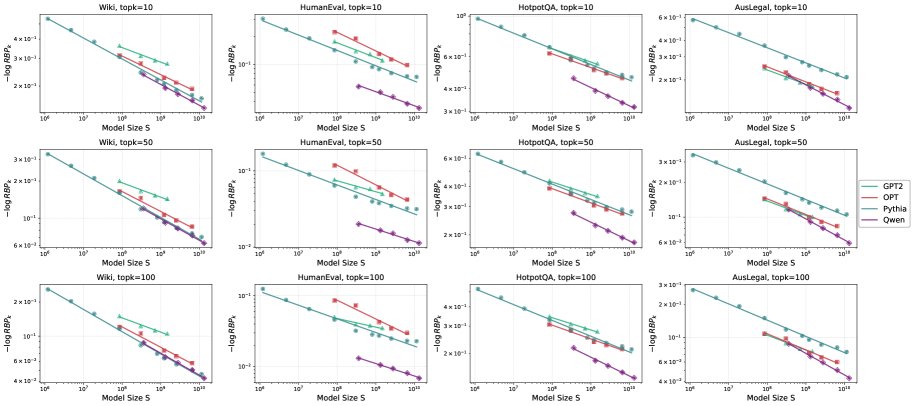
在该区间，\(k\) 取值如10、50、100，对应top-k采样场景。实验表明，幂律关系依然高度稳固，所有情况下的拟合优度 $R^2 \ge 0.97$。这说明随着模型增大，将正确Token排入top-k的能力也遵循可预测的幂律提升。

Refer to caption

大\(k\) Regime: \(k -> |V|\)

当 \(k\) 接近词汇表大小时（如20000或30000），幂律关系开始瓦解。数据点变得散乱，甚至出现性能随模型增大而下降的反常现象。本文推测，这可能是因为当 \(k\) 足够大时，绝大多数正确Token都会被包含在内，此时指标的波动主要受随机噪声和少数困难样本主导，破坏了规律性。

Refer to caption

总结

对不同 \(k\) 值的系统性研究表明：

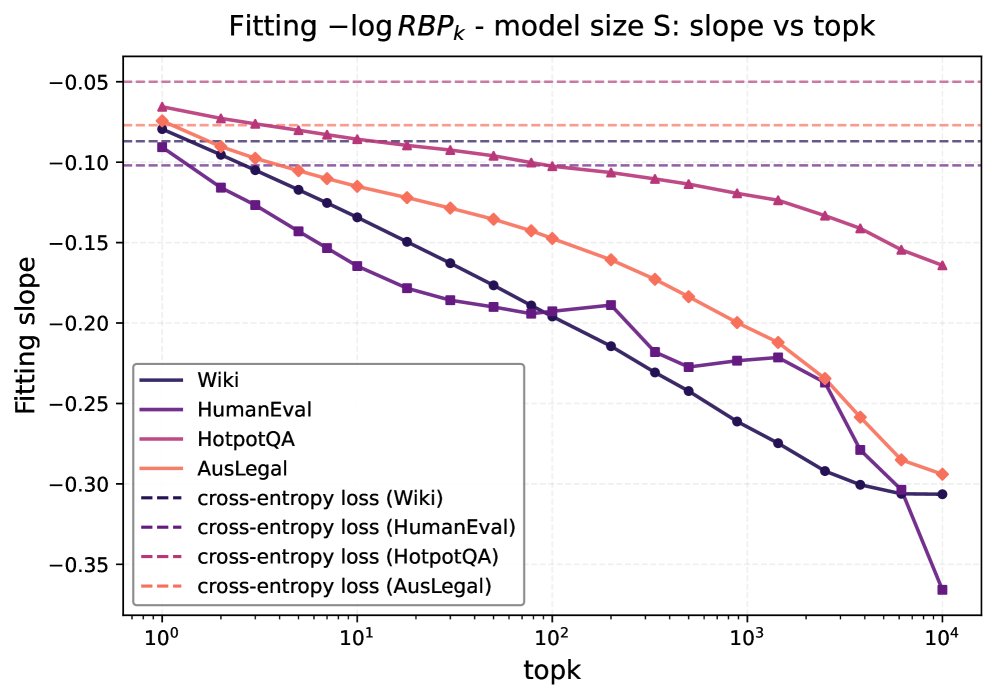
Refer to caption Refer to caption

实验结论

本文通过两个应用展示了相对标度律的价值，这些应用也构成了方法的关键实验验证和结论。

解释涌现现象

大模型在规模超过某一阈值后，在特定任务上性能会急剧提升，这种现象被称为“涌现”（emergence）。以往基于交叉熵的标度律难以解释在贪心解码或top-k采样等离散决策场景下的涌现。

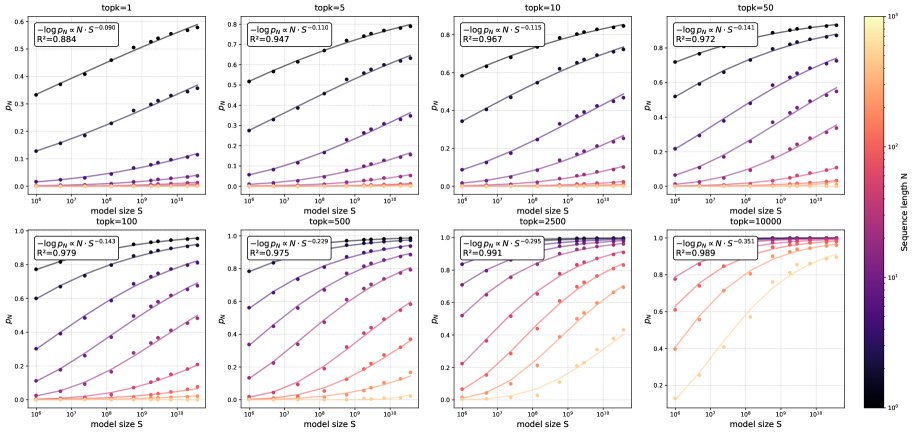
相对标度律为此提供了直接且定量的解释。假设一项任务需要模型连续 \(N\) 次将正确Token预测到top-k范围内才算成功，那么任务成功率 \(p_{N,k}\) 可以表示为：

\[\rm p_{N,k}=(\text{RBP}_{k})^{N}\]

结合相对标度律，可推导出：

\[\rm p_{N,k} \approx \exp(-C \cdot N \cdot S^{-\alpha})\]

这个公式本身就是一个S型函数（Sigmoid-like curve）。当模型规模 \(S\) 较小时，指数项很大，\(p_{N,k}\) 接近0；当 \(S\) 增大时，指数项趋于0，\(p_{N,k}\) 迅速向1攀升。序列长度 \(N\) 起到了放大器的作用，\(N\) 越大，这个性能跃迁就越陡峭，从而形成了观察到的“涌现”现象。这表明，涌现并非标度律的失效，而是Token级别平滑幂律在序列任务上的宏观体现。

Refer to caption

连接不同标度律

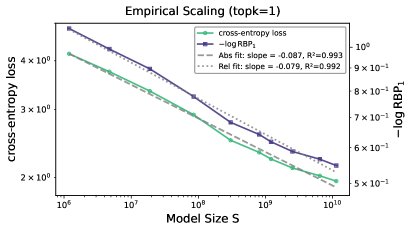
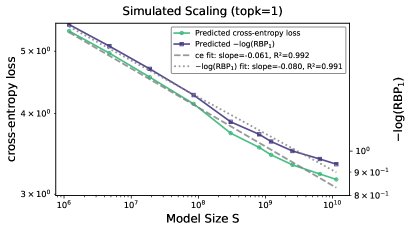
实验发现了一个奇特的现象：尽管交叉熵（绝对指标）和RBP（相对指标）衡量的是完全不同的模型性能方面，但它们的标度律行为惊人地相似。特别是当 \(k=1\) 时，$-\log(\text{RBP}_{1})$ 的标度指数与交叉熵损失的标度指数几乎完全相同（下图左）。

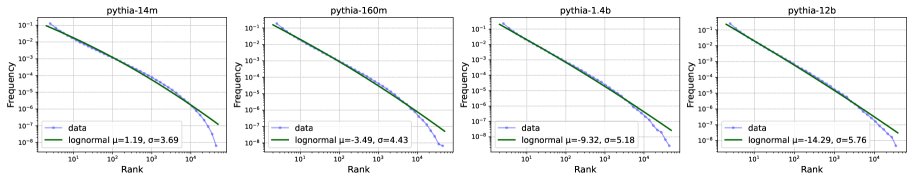
本文认为，这一巧合暗示着背后可能存在一个更深层的统一理论。作者提出了一个猜想：模型的真实标签Token的排名分布遵循对数正态分布（lognormal distribution）。如下图中所示，这一假设与真实数据拟合得很好。

基于这一猜想，可以从同一个底层的排名分布模型中，同时解析推导出交叉熵标度律和相对标度律。如下图右所示，基于该猜想预测出的两条标度律曲线与真实数据高度吻合，且展现出几乎相同的幂律衰减行为。

Refer to caption Refer to caption Refer to caption

这一发现首次将绝对指标和相对指标的标度律联系起来，提出了一个统一的概率框架，为寻找更基础的智能理论开辟了新的方向。

总结

本文引入了相对概率（RBP）指标和相对标度律，为评估和理解语言模型提供了一个关注预测“相对排序”的新视角。实验证明，该定律在不同模型和数据集上具有高度的稳健性，它不仅补充了现有交叉熵标度律的不足，还为解释“涌现”等复杂现象、探索标度律背后更深层的统一理论提供了强有力的工具和洞见。