Relative Scaling Laws for LLMs

ArXiv URL: http://arxiv.org/abs/2510.24626v1
作者: Percy Liang; William Held; David Hall; Diyi Yang
发布机构: Georgia Institute of Technology; OpenAthena; Stanford University

TL;DR

本文提出了一种名为“相对缩放定律 (Relative Scaling Laws)”的新框架，用于量化随着计算规模的增加，不同数据分布上的性能差距如何演变，揭示了规模增长并非普适的均衡器，其影响因领域而异。

图示：随着计算规模的扩大，模型性能在不同领域（左：知识领域、中：英语变体、右：AI风险行为）表现出不均衡的提升效果。

关键定义

本文的核心是建立在经典缩放定律之上，并提出了一个关键的新概念：

相对缩放定律 (Relative Scaling Laws)：一种用于衡量两个分布（一个“基准”分布和一个“处理”分布）之间性能差距随规模 $F$ (例如计算量 FLOPs) 变化的定律。它通过对两个分布的误差之比 $G(F)$ 进行幂律拟合来建模：
\[G(F)=\frac{E_{\text{treatment}}(F)}{E_{\text{baseline}}(F)}=\gamma F^{\Delta\beta}\]
其中，$E$ 是绝对误差，$\gamma$ 反映了初始的性能差距，而关键参数 $\Delta\beta = \beta_{\text{baseline}}-\beta_{\text{treatment}}$ 代表了改进速率的差异。
- 若 $\Delta\beta < 0$，处理组改进更快，差距缩小。
- 若 $\Delta\beta > 0$，处理组改进更慢，差距扩大。
- 若 $\Delta\beta = 0$，差距按比例保持不变。
IsoFLOP 训练：一种在固定计算（FLOPs）预算下训练模型的方法。在该预算下，通过调整模型大小和数据量（Token数量）的权衡，找到最优配置。本文采用此方法确保了在不同规模之间进行比较时，模型都处于其对应计算预算下的“计算最优”状态，从而避免了其他混淆变量的干扰。

本文方法

创新点

本文的核心创新在于提出了相对缩放定律，将研究焦点从模型的绝对性能转移到了不同分布间的相对性能差距上。与以往仅在某个特定规模上比较性能差距不同，该方法通过分析相对改进速率的差异（即 $\Delta\beta$ 的正负），能够预测性能差距在未来随着规模扩大是会收敛、发散还是保持不变。这为理解和预测规模增长的分布性后果提供了一个简洁而有力的量化工具。

方法基础

为了可靠地研究相对缩放定律，本文构建了坚实的方法论基础，包括模型训练和评估两个方面。

IsoFLOP 模型训练

本文训练并发布了一个由255个解码器专用Transformer模型组成的套件。这些模型在 $10^{18}$ 到 $10^{20}$ FLOPs 的固定计算（IsoFLOP）预算下进行训练，涵盖了三个不同的预训练数据集：

CommonPile：主要包含宽松许可的语料。
DCLM：完全来自经过滤和去重的高质量网络爬取数据。
Nemotron：结合了大规模真实网络数据和合成转述文本。

这种在固定计算预算下寻找模型大小和数据量最优平衡点的训练方式，确保了 scaling 曲线的稳定性和可复现性，为拟合可靠的缩放定律提供了高质量的数据基础。

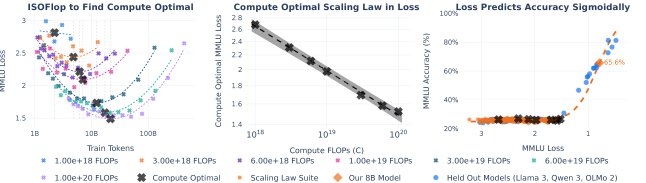
图示：对于每个FLOP预算，通过扫描Token和模型大小来选择计算最优的Token计数。沿着这些计算最优点，估计任务或子组损失如何随计算量变化。

评估协议

为了获得平滑、可预测的 scaling 曲线，本文对评估协议进行了精心设计，尤其关注能够准确反映模型能力的损失函数（loss）。

提示格式优化：在多项选择任务（如MMLU）中，标准的MCQ格式虽然准确率高，但损失曲线的预测性差；而续写格式（CF）虽然损失曲线平滑，但准确率较低。本文采用一种修改后的MCQ格式，既保留了MCQ的高准确率，又获得了CF的损失可预测性，实现了两者的平衡。

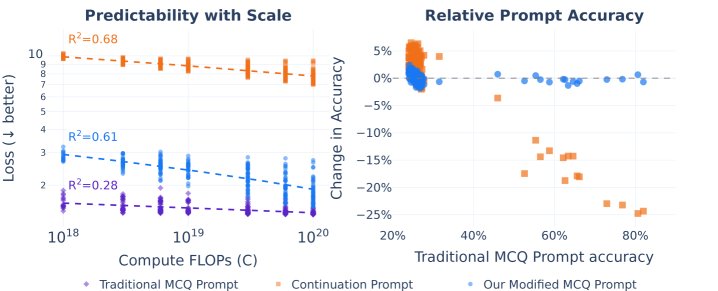
图示：不同提示格式下，由规模解释的方差程度（左）以及与标准MCQ格式的准确率差异（右）。

两阶段预测：本文采用“两阶段”方法来预测下游任务的准确率。首先，拟合计算量与损失（一种软指标）之间的缩放定律；然后，通过一个校准函数（如Sigmoid）将损失映射到最终的准确率（一种硬指标）。实验证明，损失可以作为计算量的可靠预测函数，而准确率也可以作为损失的可靠预测函数，从而建立了从计算量到最终任务性能的可靠预测链条。

图示：两阶段预测流程。左图显示了损失随计算量的幂律下降。右图显示了准确率与损失之间的Sigmoid关系，证明了损失可以有效预测准确率。

实验结论

本文通过三个案例研究展示了相对缩放定律的广泛适用性和深刻洞察力。

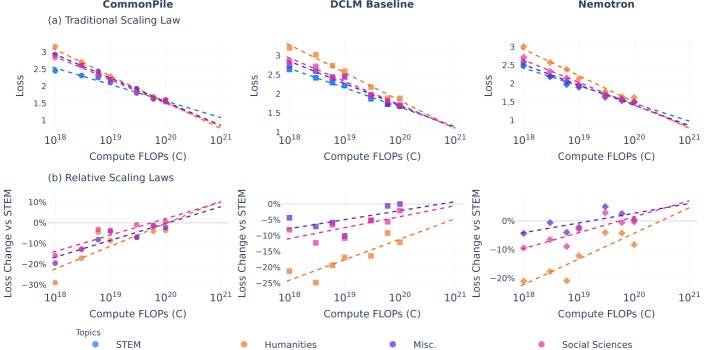
知识领域（MMLU）

在MMLU基准上，本文评估了模型在不同学术领域（STEM、人文学科、社会科学、其他）的知识扩展情况。

结果：绝对性能上，所有领域的损失都随着计算量的增加而平稳下降。从相对角度看，尽管在小规模时，模型在不同领域表现出因训练数据不同而异的初始差距（例如，基于网络的语料库更偏向STEM和商业），但随着计算规模的扩大，所有领域的性能都趋于收敛。到 $10^{20}$ FLOPs时，各领域与STEM的性能差距显著缩小。
结论：在MMLU衡量的知识领域上，规模的扩大扮演了“均衡器”的角色。这表明，虽然初始表现有别，但只要计算量足够大，模型在不同学术领域的知识差距会自然缩小。

图示：MMLU各领域 scaling。 (a) 绝对缩放定律显示所有领域的损失（BPB）都随计算量增加而下降。(b) 相对缩放定律（以STEM为基准）显示人文学科、社会科学等领域的性能差距随计算量增加而缩小，趋向于0。

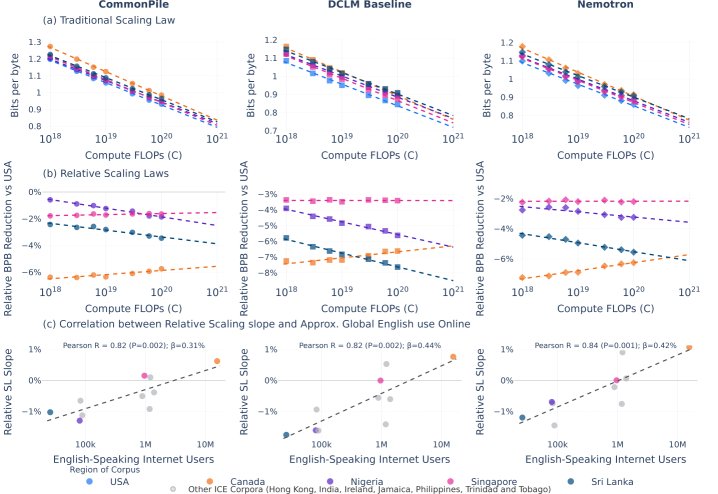
语言变体（ICE HEC）

本文使用国际英语语料库（ICE）评估了模型对不同地区英语变体的泛化能力。

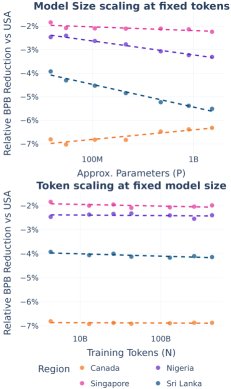
结果：绝对性能上，所有英语变体的表现都随规模扩大而提升。然而，相对性能差距的演变轨迹呈现出多样性：
- 与美国英语相比，加拿大英语的差距缩小。
- 新加坡英语的差距基本保持不变。
- 斯里兰卡和尼日利亚英语的差距则扩大。
发现：相对改进的速率与该地区在语料库收集时期（20世纪90年代）的英语互联网用户规模呈强正相关（皮尔逊相关系数 $R=0.82-0.84$）。这表明，训练数据中子群体的表征比例主要影响缩放的斜率而非初始值。
进一步分析：模型尺寸的扩大是导致相对性能差异变化的主要驱动力，而单纯增加训练数据量只会让所有变体平行提升，并不会改变它们之间的相对差距。

图示：英语变体 scaling。(a) 绝对性能提升。(b) 相对美国英语的性能差距，不同地区表现各异。(c) 相对缩放斜率与地区英语互联网用户数呈强正相关。

图示：模型尺寸缩放（上）和Token缩放（下）的对比。模型尺寸缩放导致相对性能变化，而Token缩放则使各地区性能平行提升。

AI 风险（Anthropic Evals）

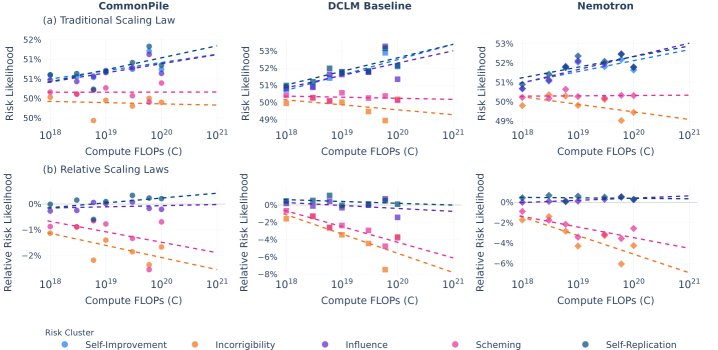
本文利用Anthropic的评估集，分析了不同AI风险行为随模型规模变化的趋势。风险被分为几大类：自我改进、影响力、自我复制、谋划（Scheming）和执拗（Incorrigibility）。

结果：风险行为的演变出现了明显的分化。
- 与能力和影响力相关的风险（如自我改进、影响力、自我复制）的可能性随着计算规模的增加而上升。
- 与对抗性相关的风险（如谋划、执拗）的可能性则没有随规模增长而出现，甚至相对于前一类风险变得更不可能。
结论：规模的扩大并非均匀地加剧所有AI风险。它选择性地放大了某些与能力和影响力相关的风险，而对抗性风险的出现则可能需要额外的条件或压力。相对缩放定律可以帮助识别哪些风险在预训练阶段就需优先关注和缓解。

图示：AI风险 scaling。(a) 各种风险行为的可能性随计算量变化。(b) 以“自我改进”为基准的相对变化，显示出“谋划”和“执拗”等对抗性风险的可能性相对下降。

总结

本文提出的相对缩放定律是一个研究规模如何影响分布鲁棒性的原则性方法。实验表明，规模的影响是多样的：在某些领域它能弥合差距，在另一些领域则可能加剧差距或产生复杂的分化。因此，在评估和优先处理鲁棒性及安全挑战时，仅仅进行单点性能比较是不够的，衡量和预测这些相对差距的演变趋势至关重要。