Repurposing Synthetic Data for Fine-grained Search Agent Supervision
-
ArXiv URL: http://arxiv.org/abs/2510.24694v1
-
作者: Yong Jiang; Maojia Song; Pengjun Xie; Xixi Wu; Kewei Tu; Jingren Zhou; Zhuo Chen; Chenxi Wang; Kuan Li; Xinyu Wang; 等13人
-
发布机构: Alibaba Group; Tongyi Lab
TL;DR
本文提出了一种名为 E-GRPO 的新方法，通过重利用合成数据生成过程中被忽略的实体信息，构建了一个细粒度的实体感知奖励函数，以解决传统强化学习方法中的奖励稀疏和“功亏一篑”（near-miss）问题，从而更有效地训练搜索智能体。
关键定义
- “功亏一篑”问题 (Near-miss Problem)：指智能体在推理过程中基本正确（例如，找到了所有关键的中间实体），但最终答案错误。传统的强化学习方法（如GRPO）会将这种“功亏一篑”的尝试与完全错误的尝试同等惩罚，从而忽视了其中有价值的学习信号。
- 实体匹配率 (Entity Match Rate, $\gamma_i$): 本文提出的一个度量标准，用于衡量单次推理（rollout）的质量。它被定义为智能体在思考（thought）过程中找到的基准（ground-truth）实体数量与问题所包含的总基准实体数量之比。
- 归一化实体匹配率 (Normalized Entity Match Rate, $\hat{\gamma}_i$): 为了在不同问题间进行稳健比较，将单次推理的原始实体匹配率 $\gamma_i$ 与其所在组内的最大匹配率 $\gamma_{\max}$ 进行归一化处理。这使得所有推理的匹配率得分能被统一在 0 到 1 的范围内。
- 实体感知奖励 (Entity-aware Reward)：E-GRPO 方法的核心。与 GRPO 的二元奖励（正确为1，错误为0）不同，该奖励函数会为错误的推理分配一个与其归一化实体匹配率 $\hat{\gamma}_i$ 成正比的奖励值（由超参数 $\alpha$ 控制）。这为训练提供了更密集的奖励信号。
- 实体感知组相对策略优化 (Entity-aware Group Relative Policy Optimization, E-GRPO)：本文提出的新型强化学习框架。它将实体感知奖励整合到 GRPO 的优化目标中，通过区分不同质量的失败轨迹，为搜索智能体的训练提供更精细的监督。
相关工作
目前，训练大型语言模型（LLM）驱动的自主智能体的主流范式是，首先通过合成数据生成技术创造大量复杂的问答数据，然后使用强化学习方法，特别是组相对策略优化（Group Relative Policy Optimization, GRPO）进行训练。
然而，这一范式存在关键瓶颈：GRPO 及其变体通常依赖于基于最终结果的奖励机制（即答案正确则奖励为1，错误则为0）。这种稀疏的奖励信号忽略了合成数据时精心嵌入的中间实体信息，导致了“奖励稀疏问题”。对于搜索智能体而言，这意味着模型无法区分“功亏一篑”（推理过程大部分正确但答案错误）和“完全失败”（从一开始就理解错问题）这两种性质截然不同的负样本。由于同等惩罚这两种情况，宝贵的学习信号被浪费，模型被迫重新学习已经掌握的推理步骤。
虽然引入细粒度的过程级监督（如过程奖励模型 PRM）是解决该问题的一个思路，但在开放式的网页搜索场景中，标注成本过高且计算上不现实。
因此，本文旨在解决一个具体问题：如何在计算成本可控的前提下，为搜索智能体获取一个细粒度且信息丰富的奖励信号。本文的核心洞察在于，答案就隐藏在现有方法所丢弃的信息中——即合成数据生成过程中的实体，可以被重新利用作为一种高质量的奖励信号。
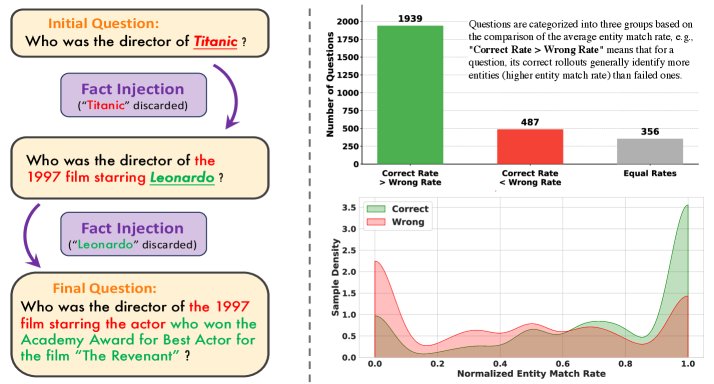左图展示了以实体为中心生成合成数据的示例。右图分析了实体匹配与智能体表现之间的相关性。
本文方法
方法动机：实体匹配率与智能体表现的强相关性
本文的出发点是，在合成数据生成过程中作为事实骨架的实体，可以作为衡量智能体推理质量的指标。为了验证这一假设，本文首先进行了实证分析。
度量标准
本文定义了两个关键指标来量化实体匹配程度：
-
实体匹配率 ($\gamma_i$)：对于一个包含 $m$ 个基准实体 $E_q$ 的问题，某一次推理 $\mathcal{H}^{(i)}$ 的实体匹配率被定义为在其所有思考步骤 $\mathcal{T}^{(i)}$ 中匹配到的实体数量与总实体数 $m$ 的比值。
\[\gamma_i = \frac{ \mid E_{\text{matched}}^{(i)} \mid }{ \mid E_q \mid } = \frac{ \mid E_{\text{matched}}^{(i)} \mid }{m}\]其中 $E_{\text{matched}}^{(i)}$ 是在思考文本中精确匹配到的实体集合。
-
归一化实体匹配率 ($\hat{\gamma}_i$)：为了跨问题比较，将单次推理的原始匹配率 $\gamma_i$ 除以该问题所在组内所有推理中的最大匹配率 $\gamma_{\max}$。
\[\hat{\gamma}_i = \begin{cases} \frac{\gamma_i}{\gamma_{\max}} & \text{if } \gamma_{\max} > 0 \\ 0 & \text{otherwise} \end{cases} \quad \text{where} \quad \gamma_{\max} = \max_{j\in\{1,\ldots,G\}} \gamma_j\]
分析结果
分析发现，实体匹配率与最终答案的正确性高度相关。在绝大多数问题中，正确推理的平均实体匹配率远高于错误推理。更重要的是，错误样本的归一化实体匹配率呈现双峰分布：大量样本匹配率为0（完全失败），但也有相当一部分样本匹配率较高，这部分正是信息丰富的“功亏一篑”型样本。
这个分析证明，实体匹配率不仅是一个简单的“通过/失败”指标，而是一个能够区分失败推理质量的细粒度标尺，为优化智能体提供了丰富的信号。
E-GRPO：实体感知组相对策略优化
基于上述发现，本文提出了实体感知组相对策略优化（E-GRPO）框架，它通过将实体匹配率直接融入奖励函数来改进策略学习。
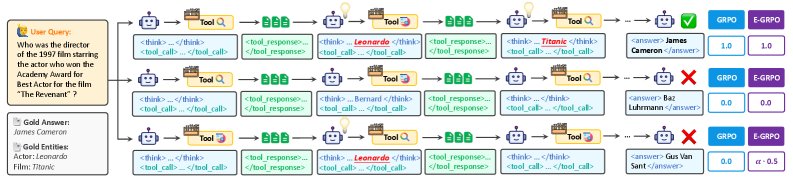GRPO 仅依赖于最终结果的奖励，而 E-GRPO 额外为负样本根据其归一化实体匹配率 $\hat{\gamma}$ 分配奖励。图中三个推理轨迹分别代表成功、完全失败和“功亏一篑”。
创新点：实体感知的奖励函数
传统 GRPO 的奖励函数是二元的（$R_i \in {0, 1}$），这使得它无法区分图中匹配了0个实体的“完全失败”和匹配了1个实体的“功亏一篑”。
E-GRPO 通过引入一个实体感知的奖励函数来解决此问题：
\[R_i = \begin{cases} 1 & \text{if } \mathcal{H}^{(i)} \text{ is correct} \\ \alpha \cdot \hat{\gamma}_i & \text{if } \mathcal{H}^{(i)} \text{ is wrong} \\ 0 & \text{if error occurs in } \mathcal{H}^{(i)} \end{cases}\]其中，$\alpha \in [0, 1]$ 是一个超参数，用于平衡最终答案准确性和实体匹配的重要性。本文使用归一化的匹配率 $\hat{\gamma}_i$ 而非原始值，以确保在不同问题组之间奖励尺度的稳定性。
优点
该奖励函数设计带来了两大优势：
- 密集的奖励谱：它为错误的推理创造了一个连续的奖励范围。如图所示，找到一个正确实体的“功亏一篑”型推理会得到一个正向奖励（$\alpha \cdot 0.5$），而完全失败的推理则奖励为零。这使得模型能够从有价值的失败中学习。
- 在全错组中提供学习信号：当一个组内的所有推理都失败时，标准 GRPO 的奖励全为0，无法产生有效的学习梯度。而 E-GRPO 仍然可以根据实体匹配率的差异提供有意义的梯度，指导模型朝向匹配更多实体的方向优化。
整体训练目标
这个经过改进的奖励 $R_i$ 被用于计算一个更具信息量的优势函数 $\hat{A}_{i,j}$，并最终被整合进 GRPO 的优化目标中，通过最大化以下目标函数来优化策略 $\pi_\theta$：
\[\mathcal{J}(\theta) = \mathbb{E}_{(q,gt)\sim\mathcal{D}, \{\mathcal{H}^{(i)}\}_{i=1}^{G}\sim\pi_{\theta_{\text{old}}}} \Bigg[\frac{1}{\sum_{i=1}^{G} \mid \mathcal{H}^{(i)} \mid }\sum_{i=1}^{G}\sum_{j=1}^{ \mid \mathcal{H}^{(i)} \mid }\min\Big(r_{i,j}(\theta)\hat{A}_{i,j},\text{clip}(r_{i,j}(\theta),1-\varepsilon_{\text{low}},1+\varepsilon_{\text{high}})\hat{A}_{i,j}\Big)\Bigg]\]其中 $r_{i,j}(\theta)$ 是重要性采样率。通过这种方式，E-GRPO 迫使模型不仅要避免错误，更要学习识别和整合关键信息的过程。
实验结论
本文在 11 个基准测试上进行了广泛评估，涵盖了问答（QA）和深度研究任务，使用了不同规模的模型（7B, 30B）和两种环境（本地模拟环境 Local、真实网络环境 Web）。
主要结果
在标准QA基准上的综合表现。带 $\ddagger$ 的结果来源于 Gao et al. (2025)。每个评估环境的最高分用粗体表示。
| 环境 | 模型 | 2Wiki. | HQA | Bamb. | Musi. | NQ | TQ | PopQA | 平均 |
|---|---|---|---|---|---|---|---|---|---|
| Local | Local-7B-SFT | 74.0 | 66.7 | 72.8 | 30.2 | 49.8 | 78.4 | 49.6 | 60.2 |
| Local-7B-GRPO | 75.1 | 65.1 | 74.4 | 31.2 | 51.5 | 82.0 | 50.5 | 61.4 | |
| Local-7B-E-GRPO | 78.5 | 68.2 | 74.6 | 33.6 | 52.3 | 83.1 | 50.1 | 64.2 | |
| Web | R1-Searcher-7B | 69.4 | 61.6 | 72.0 | 25.3 | 48.7 | 79.5 | 45.2 | 57.4 |
| DeepResearcher-7B | 64.1 | 61.0 | 76.8 | 24.5 | 52.9 | 82.8 | 45.7 | 58.3 | |
| Search-R1-32B | 69.3 | 64.2 | 81.6 | 30.8 | 51.1 | 86.6 | 53.6 | 62.5 | |
| Simple-DS-QwQ | 80.3 | 67.5 | 83.2 | 32.9 | 55.3 | 90.2 | 47.8 | 65.3 | |
| ASearcher-14B‡ | 79.8 | 70.5 | 80.8 | 33.8 | 55.4 | 88.5 | - | 65.6 | |
| Local-7B-E-GRPO | 77.2 | 71.2 | 84.3 | 34.7 | 57.7 | 90.4 | 50.9 | 67.8 |
在四个具有挑战性的深度研究基准上的综合表现。带 $\dagger$ 的结果来源于 Wu et al. (2025c)。参数量 $\leq 32$B 的智能体中，前两名的 Pass@1 分数用粗体和下划线表示。我们的智能体的最高 Pass@3 分数用粗体表示。
| 模型 | GAIA | BrowseComp | BrowseComp-ZH | xbench-DS |
|---|---|---|---|---|
| Pass@1 | Pass@3 | Pass@1 | Pass@3 | Pass@1 | Pass@3 | Pass@1 | Pass@3 | |
| OpenAI-o3 | 70.5 | - | 50.9 | - | 58.1 | - | 66.7 | - |
| Claude-4-Sonnet | 68.3 | - | 12.2 | - | 29.1 | - | 64.6 | - |
| Kimi-K2 | 57.7 | - | 14.1 | - | 28.8 | - | 50.0 | - |
| DeepSeek-V3.1 | 63.1 | - | 30.0 | - | 49.2 | - | 71.0 | - |
| R1-Searcher-7B | 20.4 | - | 0.4 | - | 0.6 | - | 4.0 | - |
| WebThinker-RL | 48.5 | - | 2.8 | - | 7.3 | - | 24.0 | - |
| WebDancer-QwQ† | 50.5 | - | 3.8 | - | 18.0 | - | 39.0 | - |
| WebSailor-7B | 37.9 | - | 6.7 | - | 14.2 | - | 34.3 | - |
| WebSailor-32B† | 51.5 | - | 10.5 | - | 25.5 | - | 47.0 | - |
| Web-7B-SFT | 31.7 | 44.7 | 5.7 | 10.5 | 13.2 | 25.6 | 37.3 | 55.0 |
| Web-7B-GRPO | 33.0 | 44.7 | 6.3 | 11.7 | 17.5 | 31.5 | 40.7 | 56.0 |
| Web-7B-E-GRPO | 35.0 | 51.5 | 7.1 | 12.4 | 18.0 | 33.3 | 42.0 | 60.3 |
| Web-30B-SFT | 45.0 | 60.2 | 10.8 | 18.5 | 23.8 | 38.1 | 43.7 | 63.0 |
| Web-30B-GRPO | 47.6 | 62.1 | 11.7 | 18.9 | 25.8 | 38.8 | 45.3 | 65.0 |
| Web-30B-E-GRPO | 49.5 | 67.0 | 12.9 | 20.2 | 26.4 | 41.7 | 47.3 | 66.3 |
- 准确性优势: E-GRPO 在所有设置下均显著优于 GRPO 基线。例如，在 Local 环境中，\(Local-7B-E-GRPO\) 的平均分比 GRPO 高出 2.8 分。在更具挑战性的深度研究基准上，\(Web-30B-E-GRPO\) 在多个任务上成为表现最好的开源模型。
- 效率和泛化性优势: 训练动态分析表明，E-GRPO 学习到了更高效的推理策略，其完成任务所需的工具调用次数持续少于 GRPO。更引人注目的是，在 Local 环境下训练的 E-GRPO 模型，在真实的 Web 环境中进行评估时，其性能依然超越了所有同类模型，展现了极强的泛化能力。
- 探索能力优势 (Pass@3): E-GRPO 在 Pass@3 指标上取得了巨大提升。这说明实体感知奖励鼓励模型探索那些有前景但尚不完美的推理路径，从而增加了在多次尝试中找到正确答案的概率。
训练动态与消融研究
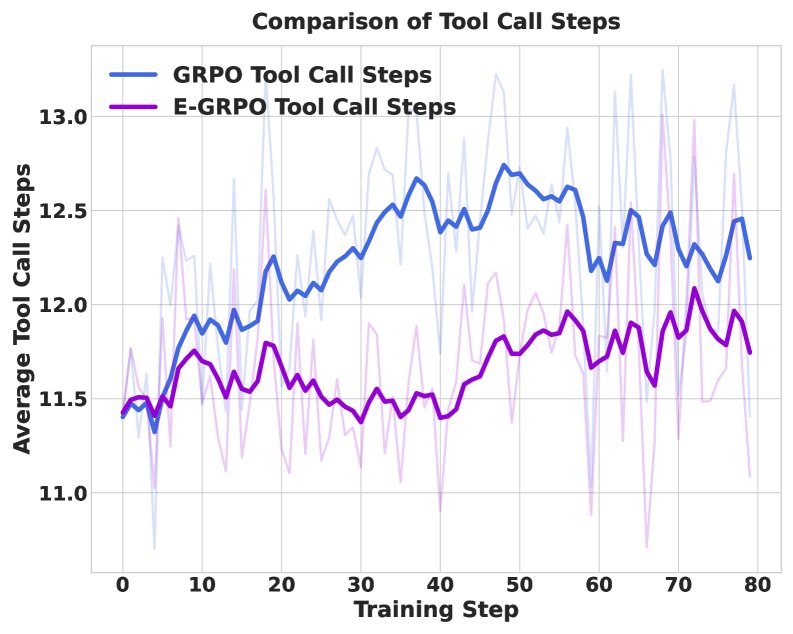
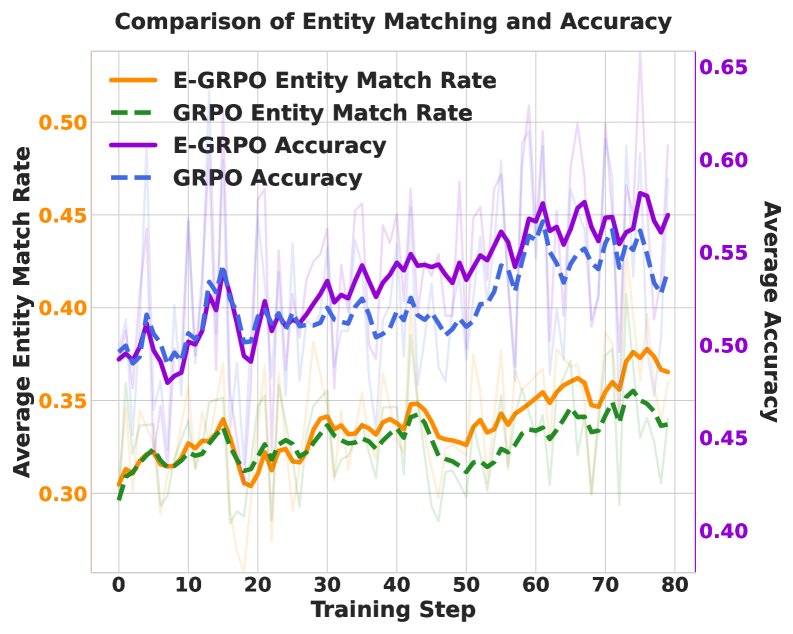
- 训练动态分析: 上图显示，E-GRPO（紫色线）的训练准确率稳步上升，始终高于 GRPO（蓝色线）。同时，E-GRPO（紫色线）所需的工具调用步骤更少，证明了其学习效率。右图证实了核心假设：实体匹配率（橙色/绿色线）与最终准确率（紫色/蓝色线）同步增长，而 E-GRPO 通过直接激励实体匹配，获得了更高的匹配率，并最终转化为更高的准确率。
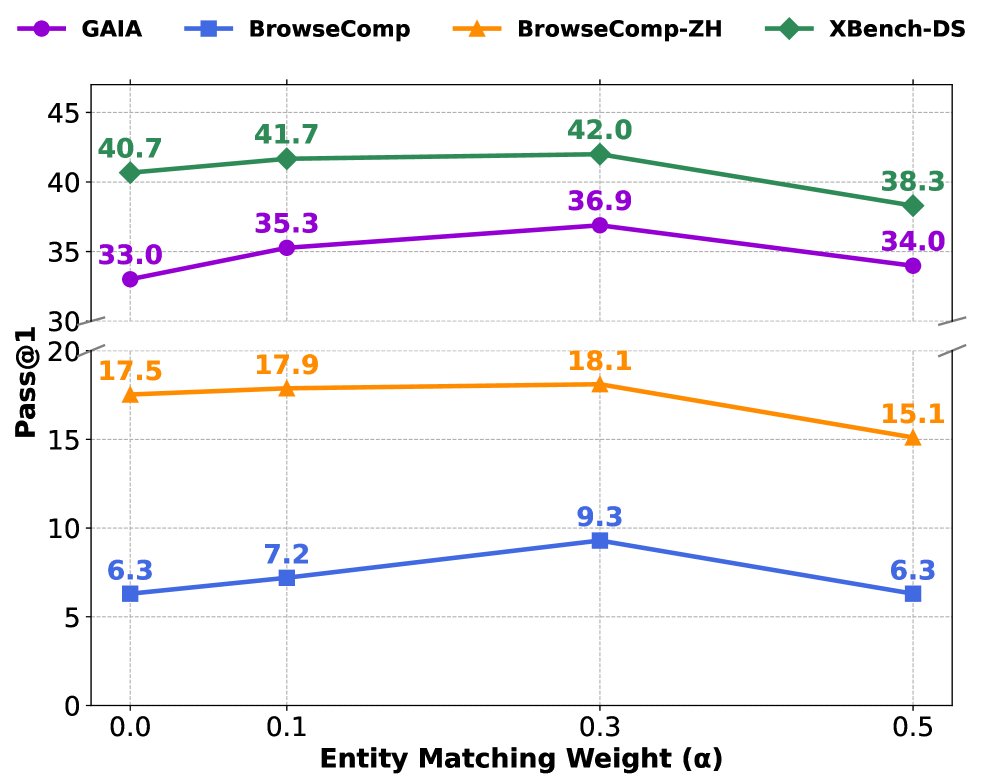
- 超参数$\alpha$的影响: 消融实验表明，当 $\alpha$ 从0（即标准GRPO）增加到0.3时，模型性能持续提升，证明了实体感知奖励的有效性。但当 $\alpha$ 进一步增加到0.5时，性能出现下降，这表明过度关注中间实体匹配可能会分散模型对最终答案正确性的注意力。实验确定 $\alpha=0.3$ 是一个平衡点。
总结
实验结果强有力地证明，E-GRPO 通过利用合成数据中被忽略的实体信息，构建了一个有效的细粒度奖励机制。该方法不仅在准确性上全面超越了传统的 GRPO 方法，还使智能体学会了更高效、更具泛化性的推理策略，尤其在需要深度探索的复杂任务中表现出显著优势。