RiskPO: Risk-based Policy Optimization via Verifiable Reward for LLM Post-Training

TL;DR

本文提出一种名为 RiskPO 的大语言模型训练后优化方法，通过引入一个基于风险度量的目标函数（MVaR），替代传统的均值优化目标，从而将模型优化的重点放在处理困难样本上，有效缓解了熵坍塌问题，并显著提升了模型的推理能力。

关键定义

相关工作

当前，带有可验证奖励的强化学习（RLVR）已成为提升大语言模型（LLM）推理能力的主流后训练技术。其中的代表性方法，如组相对策略优化 (Group Relative Policy Optimization, GRPO)，通过最大化平均奖励来提升模型性能。

然而，这些基于均值优化的方法存在一个核心瓶颈：熵坍塌 (entropy collapse)。在训练早期，模型的策略熵会迅速下降，导致模型变得过度自信、过早停止探索，性能提升很快陷入停滞。这种现象限制了模型学习新知识和新推理路径的能力，其性能提升更多体现在对已知答案的高效采样上，而非真正扩展其内在的推理能力边界。

因此，本文旨在解决现有RLVR方法因优化平均性能而导致的熵坍塌和推理能力提升有限的问题。

本文方法

本文提出了基于风险的策略优化 (Risk-based Policy Optimization, RiskPO) 方法，其核心思想是用风险敏感的目标函数替代传统的均值目标，从而引导模型关注并解决更具挑战性的问题。

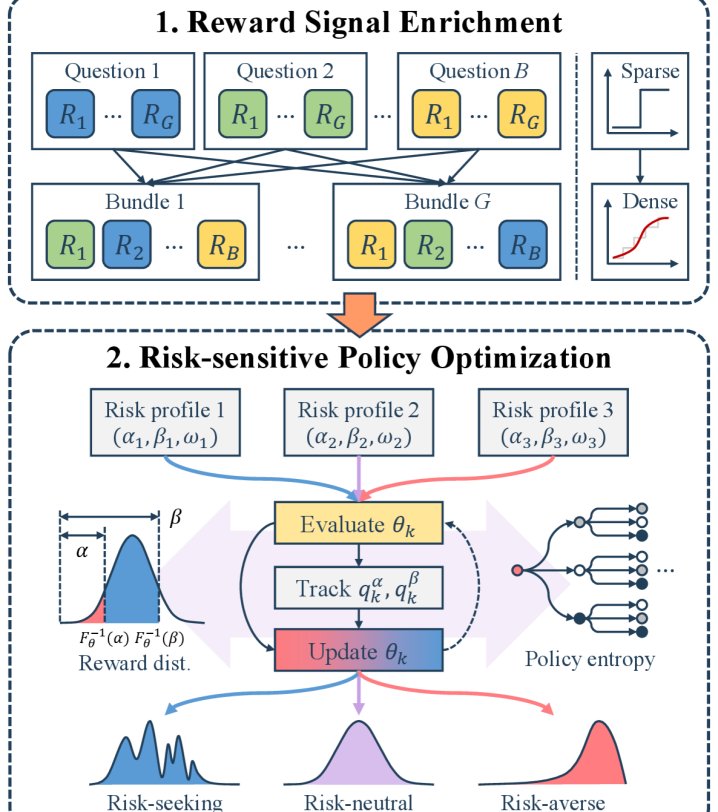
RiskPO框架

创新点

RiskPO的核心创新在于引入了混合风险价值 (Mixed Value-at-Risk, MVaR) 目标，并结合了问题捆绑 (Bundling) 机制。

  1. 从均值到风险：MVaR目标函数 传统的RLVR方法优化期望奖励 $\mathbb{E}[R(y)]$，这容易忽略那些虽然回答错误但具有学习价值的“困难”样本。为了解决这个问题，本文首先引入了区间风险价值 (Range Value-at-Risk, RVaR)，它衡量的是奖励分布在特定分位区间 $[\alpha, \beta]$ 内的条件期望：

    \[\mathcal{J}_{\text{RVaR}_{\alpha:\beta}}(\theta) := \mathbb{E}\big[R(y) \mid R(y)\in[F^{-1}_{\theta}(\alpha),F^{-1}_{\theta}(\beta)]\big]\]

    在此基础上，本文进一步提出了MVaR，它对奖励分布的尾部（即表现最差的部分）给予了额外的关注。MVaR可以表示为：

    \[\mathcal{J}_{\text{MVaR}^{\omega}_{\alpha:\beta}}(\theta) = (1+\omega)\alpha\mathcal{J}_{\text{RVaR}_{0:\alpha}}(\theta)+(\beta-\alpha)\mathcal{J}_{\text{RVaR}_{\alpha:\beta}}(\theta)\]

    其中，$\omega \geq 0$ 是一个超参数，用于增强对最低分位区间 $[0, \alpha]$ （即最困难的样本）的优化权重。通过这种方式，MVaR能够放大来自低奖励答案的梯度信号，迫使模型减少过度自信，并探索新的推理策略。

  2. 信号增强：问题捆绑机制 由于单个问题的奖励信号是二元的（0或1），信息非常稀疏，难以形成有效的分布来进行风险度量。为了解决这一问题，本文设计了问题捆绑机制：将 $B$ 个不同的问题聚合成一个“捆绑包”（bundle），并将这个捆绑包的总得分（即正确回答的问题数量）作为奖励信号 $R_B$。

    \[R_B = \sum_{i=1}^{B} R(y^i)\]

    这种聚合方式将稀疏的二元反馈转化为了一个取值范围为 ${0, 1, \dots, B}$ 的更丰富的奖励分布，从而能够更精细地区分不同水平的表现，并有效避免了当所有答案都错误时梯度消失的问题。

算法实现

RiskPO的完整算法将MVaR目标和问题捆绑机制结合，并采用了PPO中常用的信任域更新策略以保证训练稳定。具体而言，其最终的优化目标如下：

\[\mathcal{J}_{\mathrm{MVaR}}^{\mathrm{clip}}(\theta)=\mathbb{E}_{X,Y,\{\xi_{i}\}}\bigg[\frac{1}{G}\sum_{j=1}^{G}\frac{1}{B}\sum_{i=1}^{B}\min\!\Big(s^{i}_{j}(\theta)\,A^{(j)},\;\text{clip}(s^{i}_{j}(\theta),1-\epsilon,1+\epsilon)\,A^{(j)}\Big)\bigg]\]

其中，$A^{(j)}$ 是基于MVaR计算的捆绑包级别的优势函数（advantage），$s^{i}_{j}(\theta)$ 是序列级别的重要性采样率。算法在训练中会动态追踪奖励分布的分位点 $F_{\theta}^{-1}(\alpha)$ 和 $F_{\theta}^{-1}(\beta)$，以实现端到端的优化。

理论分析：熵机制

本文从理论上证明了RiskPO为何能缓解熵坍塌。核心结论是，策略熵的变化与优势函数 $A(x,y)$ 和对数概率 $\log\pi_{\theta}(y \mid x)$ 的协方差呈负相关关系：

\[\mathcal{H}\!\left(\pi_{\theta_{k+1}} \mid x\right)-\mathcal{H}\!\left(\pi_{\theta_{k}} \mid x\right)\;=\;-\eta\,\operatorname{Cov}_{y\sim\pi_{\theta_{k}}(\cdot \mid x)}\!\big(\log\pi_{\theta_{k}}(y \mid x),\,A_{\theta_{k}}(x,y)\big)\;+\;O\!\left(\ \mid \Delta_{k}\ \mid ^{2}\right)\]

本文通过实证和理论分析指出，相比于传统均值目标，MVaR目标的优势函数 $A_{\mathrm{MVaR}}$ 与对数概率的协方差更小：

\[\mathrm{Cov}_{y\sim\pi_{\theta}(\cdot \mid x)}(\log\pi_{\theta}(y \mid x),A_{\mathrm{MVaR}_{\alpha:\beta}^{\omega}})\leq\mathrm{Cov}_{y\sim\pi_{\theta}(\cdot \mid x)}(\log\pi_{\theta}(y \mid x),A_{\mathrm{Mean}})\]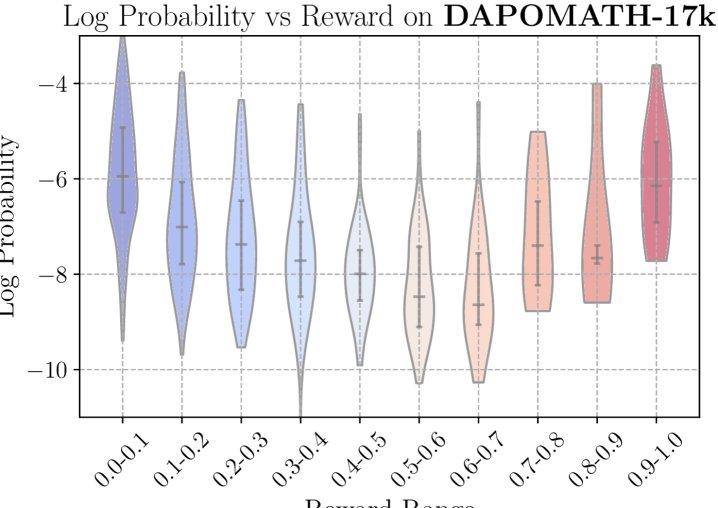

对数概率与奖励分位水平的关系 这意味着使用MVaR目标的梯度更新步骤对熵的负面影响更小，从而能够有效减缓熵的下降速度，保持模型的探索能力。

实验结论

本文在数学推理、代码生成和多模态推理等多个基准测试上进行了广泛实验，验证了RiskPO的有效性。

性能提升


方法 AIME (Test) AIME (Internal) AMC (Test) AMC (Internal) MATH500 (Test) MATH500 (Internal) 平均分
GRPO-1.5B 20.0 20.0 56.6 79.2 27.1 39.6 40.41
DAPO-1.5B 30.0 26.6 58.6 78.2 29.2 40.6 43.87
RiskPO (本文) 36.6 33.3 59.2 80.5 30.3 40.0 46.65



方法 MATH GSM8K 平均 (数学) LiveCodeBench Geometry3K 平均 (多领域)
GRPO 54.3 78.8 66.55 25.8 53.7 39.75
DAPO 55.2 80.3 67.75 26.2 54.3 40.25
RiskPO (本文) 56.5 80.6 68.55 26.9 55.4 41.15


扩展推理边界

实验比较了不同$k$值下的Pass@k指标。结果显示，随着$k$的增大，RiskPO相较于GRPO的优势愈发明显。这表明RiskPO不仅是提升了对已知解的采样效率（例如将Pass@16提升至Pass@1），更是学会了解决那些基线方法即使在多次尝试下也无法解决的新问题，从而真正扩展了模型的基础推理能力边界。

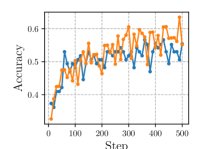
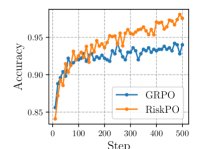
AMC和MATH500数据集上的Pass@k学习曲线 AMC和MATH500数据集上的Pass@k学习曲线 … (其他Pass@k曲线图) AMC和MATH500数据集上的Pass@k学习曲线

缓解熵坍塌

训练过程中的动态曲线验证了理论分析。如下图所示，与GRPO相比，RiskPO在整个训练过程中维持了显著更高的策略熵，有效避免了过早的熵坍塌。同时，尽管平均奖励（Mean reward）曲线相近，但RiskPO在风险度量指标上表现更优，说明其在解决困难问题上取得了更好的进展。

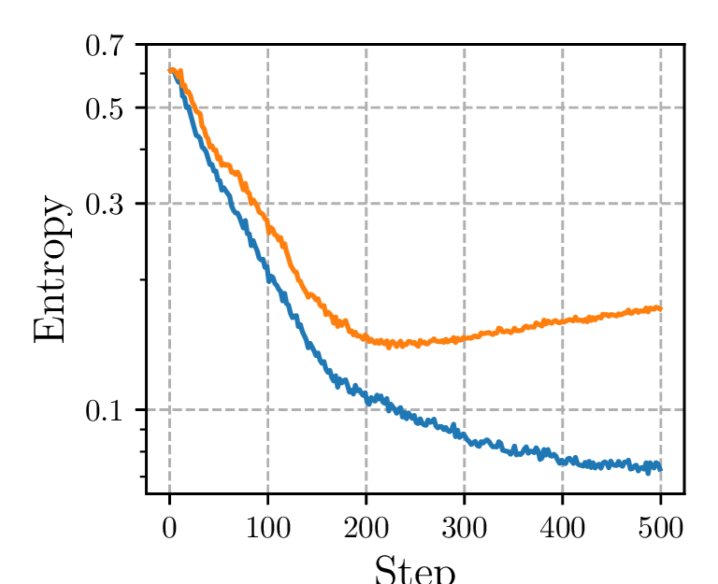
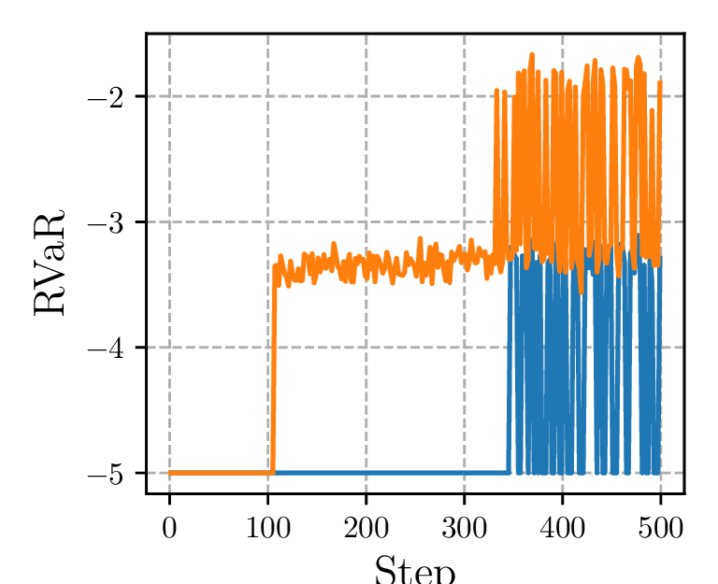
训练过程中的熵变化 训练过程中的平均奖励变化

总结

实验结果有力地证明，RiskPO通过其创新的风险敏感目标和问题捆绑机制，能够有效缓解熵坍塌，促进模型探索，并最终在多个具有挑战性的推理任务上取得超越现有方法的性能。这表明，基于风险的优化是增强LLM推理能力的一个严谨且有效的范式。