Robust Layerwise Scaling Rules by Proper Weight Decay Tuning
-
ArXiv URL: http://arxiv.org/abs/2510.15262v1
-
作者: Quanquan Gu; Zhiyuan Fan; Qingyue Zhao; Yifeng Liu
-
发布机构: MIT; UCLA
TL;DR
本文提出了一种针对矩阵类参数的权重衰减缩放规则 ($\lambda \propto \sqrt{d}$),通过在AdamW训练的稳态下保持子层增益在不同模型宽度下的不变性,从而扩展了最大更新参数化($\mu$P)框架,实现了学习率和权重衰减超参数的零样本迁移。
关键定义
本文的研究建立在最大更新参数化($\mu$P)之上,并引入了对训练动态的新理解。以下是理解本文核心思想的关键概念:
-
最大更新参数化 (Maximal-update Parameterization, $\mu$P):一个理论框架,旨在通过调整参数初始化和学习率,使得模型宽度变化时,参数更新的幅度保持不变。其核心思想是,对于不同类型的参数(向量类和矩阵类),应采用不同的缩放规则,从而实现超参数(尤其是学习率)在不同尺寸模型间的迁移。
-
优化器控制的稳态 (Optimizer-governed steady state):与$\mu$P关注的训练早期、由初始化主导的动态不同,本文指出在现代的缩放不变架构中,训练会迅速进入一个稳态。在此状态下,参数的范数(scale)主要由优化器(如AdamW)的超参数(学习率$\eta$和权重衰减$\lambda$)共同决定,而非初始化方差。
-
子层增益 (Sublayer gain):定义为一个层(sublayer)的输出激活值的均方根范数(RMS norm)与输入激活值均方根范数的比值,即 $\ \mid \mathbf{y}\ \mid _{\mathrm{rms}}/\ \mid \mathbf{x}\ \mid _{\mathrm{rms}}$。本文的核心目标是通过调整权重衰减来保持该增益在模型宽度变化时不发生改变,从而维持稳定的训练动态。
-
参数类别 (Parameter Classes):根据参数尺寸随模型宽度 $d$ 的变化方式,将参数分为两类:
- 向量类参数 (Vector-like parameters):参数数量与 $d$ 呈线性关系,如嵌入层、RMSNorm增益、偏置项等。
- 矩阵类参数 (Matrix-like parameters):参数数量与 $d$ 呈二次关系,如注意力机制和前馈网络中的投影矩阵。本文提出的新权重衰减规则主要针对此类参数。
相关工作
当前,大规模模型的设计主要遵循两种思路:一是宏观的经验性缩放定律 (Empirical scaling laws),它们描述了模型性能与模型大小、数据量和计算预算之间的幂律关系,指导“分配什么”资源;二是微观的最大更新参数化 ($\mu$P),它通过保持参数更新幅度的宽度不变性,解决了“如何迁移”超参数(主要是学习率)的问题。
然而,$\mu$P的理论分析主要局限于训练的早期近初始化阶段。在现代使用了归一化层(如LayerNorm)的缩放不变架构中,训练很快会进入一个由优化器决定的稳态。在这个阶段,归一化层虽然保证了前向传播的尺度不变性,但却引入了反向传播的尺度敏感性:归一化层的梯度会反比于其输入的尺度。由于不同宽度的模型在稳态下的激活值尺度不同,这导致了有效学习率的宽度依赖性,从而破坏了$\mu$P的超参数迁移效果。
本文旨在解决这一具体问题:如何扩展$\mu$P框架,使其在更符合实际的、由优化器主导的训练稳态下依然有效? 具体而言,作者寻求一个与$\mu$P学习率规则相匹配的权重衰减缩放规则,以稳定跨宽度的子层增益,最终实现学习率和权重衰减两种超参数的同时、鲁棒的“零样本”迁移。
本文方法
本文的核心方法是为$\mu$P框架补充一个针对权重衰减的缩放规则,以解决在训练稳态下超参数迁移失效的问题。
创新点
该方法建立在一个关键的理论和经验观察之上:在AdamW训练的稳态中,参数矩阵的范数不再由其初始化决定,而是稳定在与 $\sqrt{\eta/\lambda}$ 成正比的水平上。因此,为了在改变模型宽度 $d$ 时保持子层增益不变,必须合理地缩放权重衰减 $\lambda$ 来控制参数矩阵的范数。
1. 经验观察与规则推导
通过对LLaMA风格的Transformer模型进行实验,作者观察到以下两个关键现象:
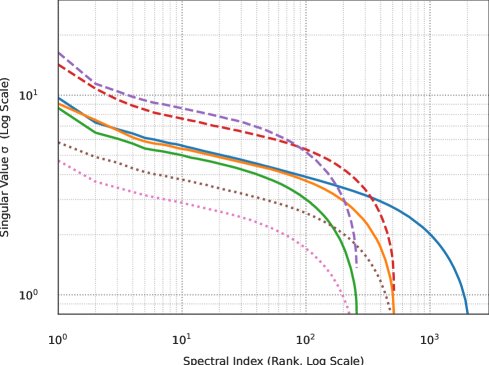
- 固定宽度下的谱缩放:在模型宽度 $d$ 固定时,参数矩阵奇异值谱的整体幅度与 $\sqrt{\eta/\lambda}$ 成正比,而其形状几乎保持不变。这意味着可以通过调整 $\eta/\lambda$ 的比值来直接控制权重矩阵的尺度,进而控制子层增益。
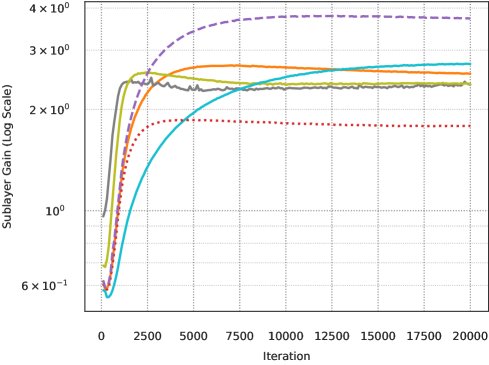
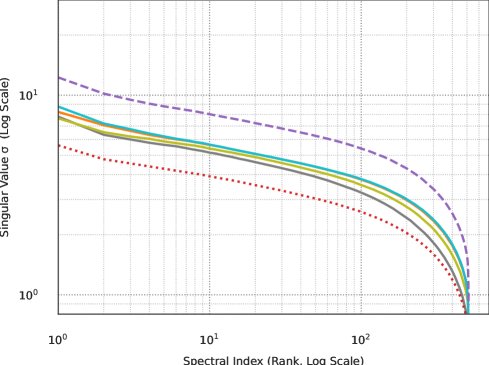
- 跨宽度的谱缩放:当模型宽度 $d$ 变化时,作者发现为了保持矩阵类参数的顶部奇异值大小不变,需要满足以下经验性关系:
这个关系确保了不同宽度模型中,关键的信号放大行为(由顶部奇异值主导)保持一致,从而实现了子层增益的宽度不变性。
2. 权重衰减缩放规则的提出
结合上述经验观察和$\mu$P为矩阵类参数设定的学习率缩放规则 $\eta_2 \propto d^{-1}$,可以推导出权重衰减 $\lambda_2$ 的缩放规则:
将 $\eta_2 \propto d^{-1}$ 代入经验公式,得到:
\[\sqrt{\frac{d^{-1}}{\lambda_2}} \propto d^{-0.75} \implies \frac{1}{\sqrt{\lambda_2 d}} \propto d^{-0.75} \implies \sqrt{\lambda_2} \propto \frac{d^{0.75}}{\sqrt{d}} = d^{0.25}\]因此,权重衰减应遵循:
\[\lambda_2 \propto \sqrt{d}\]3. 完整的层级缩放方案
综合$\mu$P和本文的发现,作者提出了一个完整的、针对不同参数类别的层级缩放方案:
| 类别 | 初始方差 | 学习率 | 权重衰减 |
|---|---|---|---|
| 向量类 | $\sigma_{1}^{2}=\Theta_{d}(1)$ | $\eta_{1}=\Theta_{d}(1)$ | $\lambda_{1}=0$ |
| 矩阵类 | $\sigma_{2}^{2}=\Theta(d^{-1})$ | $\eta_{2}=\Theta(d^{-1})$ | $\lambda_{2}=\Theta(\sqrt{d})$ |
这个方案的核心优点在于:它通过显式控制训练稳态下的参数尺度,将$\mu$P的有效性从训练早期扩展到了整个训练过程。它提供了一个理论上合理且经验上验证有效的配方,消除了为不同宽度的模型反复搜索学习率和权重衰减的巨大开销。
此外,本文还提供了一个简单的诊断方法:通过检查不同宽度模型下权重矩阵的顶部奇异值是否对齐,可以验证子层增益是否保持了不变性。

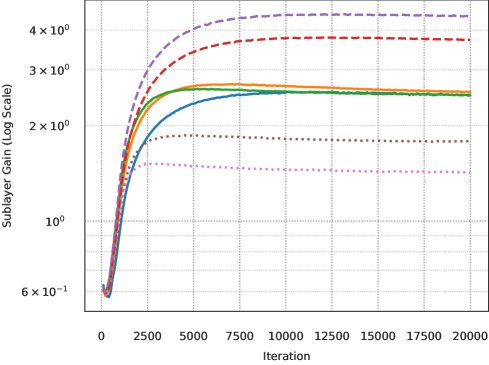
实验结论
本文通过在LLaMA风格的Transformer模型上的一系列实验,验证了所提出的权重衰减缩放规则的有效性。
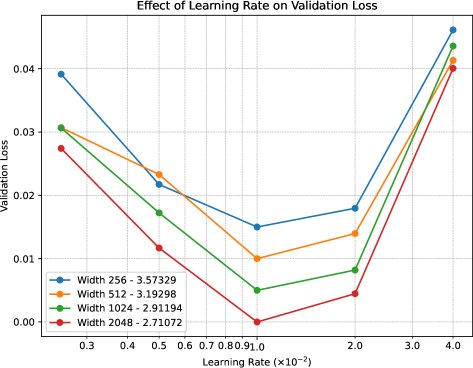
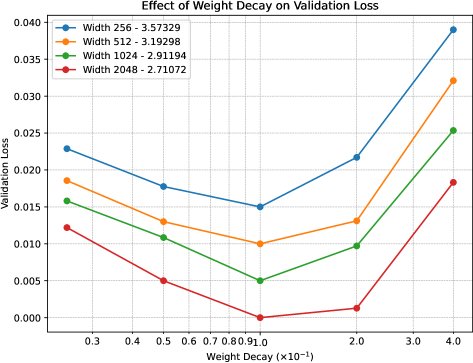
- 验证了超参数迁移的有效性:实验核心结果表明,当使用本文提出的缩放方案(即向量类参数 $\eta_1 \propto 1, \lambda_1=0$;矩阵类参数 $\eta_2 \propto d^{-1}, \lambda_2 \propto \sqrt{d}$)时,在小型代理模型(proxy model)上找到的最优基础学习率和最优基础权重衰减,可以被直接、无缝地迁移到宽度大数倍的目标模型上。如下图所示,不同宽度模型的损失曲面(loss landscape)在根据缩放规则调整后,其最小值点高度对齐,证明了“零样本”迁移的成功。
-
方法的优势领域:本文方法在需要跨越较大模型宽度进行超参数迁移的场景下表现出众,尤其适用于类似LLM预训练的、进入优化器稳态的长时间训练任务。它显著优于仅使用$\mu$P学习率规则或采用其他启发式权重衰减规则(如固定或线性缩放)的策略,后者在跨宽度迁移时会导致性能下降。
-
方法的普适性:作者在一个仅使用随机合成数据的简化环境中重复了实验,发现 $\lambda \propto \sqrt{d}$ 的规则依然成立。这表明该缩放行为是模型架构、归一化层和AdamW优化器动态相互作用产生的内在属性,而不仅仅是特定数据分布的产物。
-
最终结论:本文提出的 $\lambda_2 \propto \sqrt{d}$ 权重衰减规则,是对$\mu$P框架的一个重要补充和扩展。它解决了$\mu$P在训练稳态下因尺度敏感性而失效的问题,提供了一个在AdamW优化器下实现学习率和权重衰减联合迁移的实用、可靠的配方。这使得研究者可以从小模型上高效地调整超参数,并充满信心地将其应用于大规模模型,从而大幅节省计算资源。