s1: Simple test-time scaling
-
ArXiv URL: http://arxiv.org/abs/2501.19393v3
-
作者: Zitong Yang; Fei-Fei Li; Weijia Shi; Luke S. Zettlemoyer; Percy Liang; Emmanuel J. Candes; Xiang Lisa Li; Hanna Hajishirzi; Tatsunori Hashimoto; Niklas Muennighoff
-
发布机构: Allen Institute for AI; Contextual AI; Stanford University; University of Washington
TL;DR
本文提出了一种极其简单且高效的方法,通过在精心筛选的1000个样本(s1K)上进行监督微调,并结合一种名为“预算强制”(budget forcing)的测试时干预技术,成功构建了一个具备强大推理能力和可控测试时扩展(test-time scaling)行为的语言模型(s1-32B)。
关键定义
- 测试时扩展 (Test-time scaling): 一种提升模型性能的新范式,其核心思想是在模型的测试或推理阶段,而非训练阶段,通过增加计算资源来获得更好的结果。
- s1K 数据集: 本文精心构建的一个小型推理数据集,仅包含1000个“问题-推理链”对。其构建遵循三个核心标准:困难度(Difficulty)、多样性(Diversity)和高质量(Quality),旨在用最少的资源激活模型的推理能力。
- 预算强制 (Budget forcing): 本文提出的一种简单的解码时干预技术,用于控制模型在生成推理链(即“思考”过程)时消耗的计算预算。它包含两种操作:
- 强制终止: 当模型生成的思考过程超过预设的token上限时,强制追加结束符,使其提前输出答案。
- 强制延长: 当模型试图提前结束思考但需要其进行更多推理时,抑制其生成结束符,并向当前推理链末尾追加特定字符串(如“Wait”),鼓励模型进行复查或进一步探索,从而可能修正错误。
相关工作
当前,语言模型性能的提升主要依赖于在训练阶段大规模增加计算资源。近年来,“测试时扩展”成为一个新的研究方向,即在推理时投入更多计算来提升性能。OpenAI的o1模型验证了该范式的可行性,但其方法未公开。
这激发了大量复制o1的尝试,这些方法通常依赖于复杂的技术,如蒙特卡洛树搜索(Monte Carlo Tree Search)、多智能体(multi-agent)方法或大规模强化学习(RL),需要数百万样本和复杂的训练流程。例如,DeepSeek R1虽成功复现了o1级别的性能,但同样依赖于RL和海量数据。尽管如此,尚无一种方法能以简单、公开的方式清晰地复现出“测试时扩展”的行为。
本文旨在解决的核心问题是:实现强大的推理性能和清晰的测试时扩展行为,最简单的方法是什么?
本文方法
本文提出了一套极其简洁的流程,包含两个核心部分:一个高度样本高效的数据集构建策略和一个简单的测试时扩展技术。
1. 推理数据集构建 (s1K)
为实现“用最少资源达到最好效果”的目标,本文没有直接使用海量数据,而是精心筛选了1000个样本,命名为s1K。
初始数据收集:首先从16个来源收集了约5.9万个问题,涵盖数学竞赛、奥林匹克科学竞赛、标准化测试等领域,并利用Gemini Flash Thinking API为每个问题生成推理链。
三阶段筛选:接着,通过三个阶段的过滤,将数据从5.9万精简到1000个,遵循三大原则:
- 质量 (Quality):首先剔除有API错误或格式问题(如ASCII图表)的样本,得到约5.1万个高质量样本。
- 困难度 (Difficulty):使用两个指标来衡量难度。首先,用Qwen2.5-7B和32B模型进行预答题,剔除能被它们轻松解决的“简单”问题。其次,基于“越难的问题需要越长的思考”这一假设,将推理链的token长度作为另一个难度指标。此步骤后剩余约2.4万个样本。
- 多样性 (Diversity):为确保模型能处理不同类型的推理,使用数学学科分类系统(MSC)对问题进行领域划分(如几何、组合数学等)。然后,通过随机选择领域并从该领域中优先抽取推理链更长的问题的方式进行采样,最终得到覆盖50个不同领域的1000个样本。

最终,在Qwen2.5-32B-Instruct模型上对这1000个s1K样本进行监督微调(SFT),仅用16块H100 GPU训练26分钟,便得到了s1-32B模型。
2. 测试时扩展方法 (预算强制)
本文首先将测试时扩展方法分为两类:顺序式 (Sequential)(后续计算依赖于前期结果,如长推理链)和并行式 (Parallel)(多次独立计算后选择最优,如多数投票)。本文聚焦于更具潜力的顺序式扩展,并提出了“预算强制”这一创新方法。
创新点: 预算强制是一种在解码阶段进行的简单干预:
- 设置上限:如果模型推理过程过长,超出预算,则直接在当前生成后追加结束标记,强制模型输出最终答案。
- 设置下限:如果模型想提前结束推理,但希望它进行更多思考,则阻止它生成结束标记,并在当前文本后追加“Wait”一词。这会促使模型重新审视已有的推理步骤,经常能引导其发现并修正错误。

优点: 该方法极其简单,无需修改模型架构或进行复杂训练。实验证明,它能完美地控制计算预算,并带来稳定、正向的性能提升,优于其他通过prompt控制长度或进行拒绝采样的方法。
为了系统性地评估测试时扩展方法,本文还定义了三个关键指标:
- 控制度 (Control): 方法对计算预算(如token数)的控制精确度。
- 扩展性 (Scaling): 性能随计算预算增加而提升的平均斜率。
- 性能 (Performance): 方法能达到的最高准确率。
实验结论
本文在AIME24(美国数学邀请赛)、MATH500(竞赛数学)和GPQA Diamond(博士级科学问题)等高难度推理基准上进行了广泛实验。
关键实验结果
- 测试时扩展效果显著: s1-32B模型结合预算强制后,展现出清晰的测试时扩展行为。随着测试时计算量的增加,模型在各项任务上的性能持续提升。例如,在AIME24上,通过增加思考token,准确率从50%显著提升至57%。
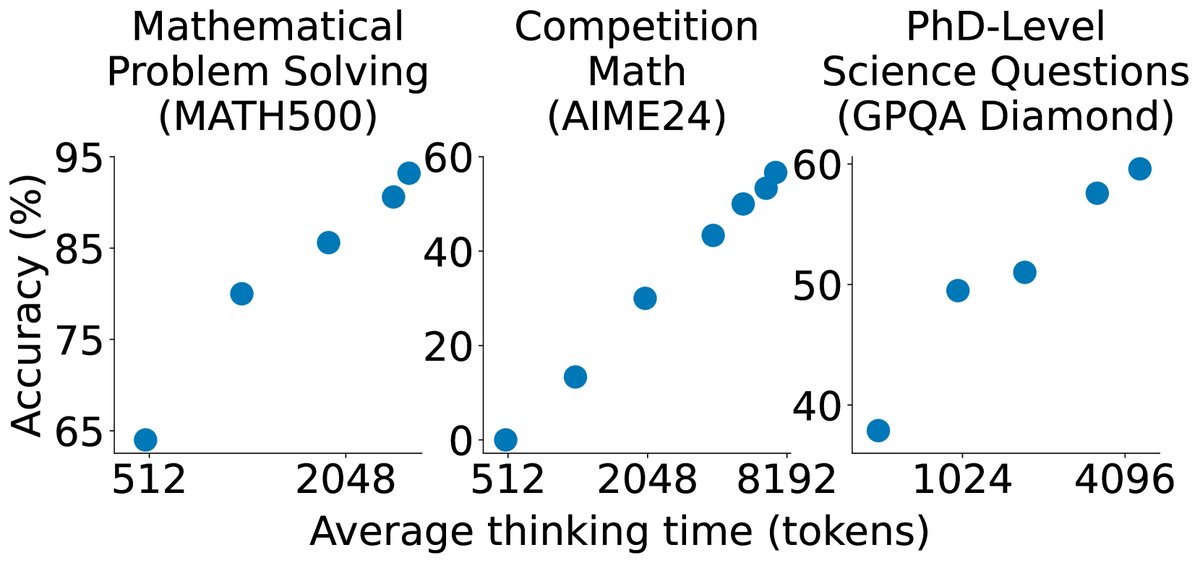
- 模型性能强大且样本高效: s1-32B仅用1000个样本微调,就在多个基准上取得了与使用数十万甚至数百万样本训练的模型相媲美的性能,甚至在部分任务上超越了o1-preview等闭源模型,是目前样本效率最高的开源推理模型之一。
| 模型 | 训练样本数 | AIME 2024 | MATH 500 | GPQA Diamond |
|---|---|---|---|---|
| API only | ||||
| o1-preview | N.A. | 44.6 | 85.5 | 73.3 |
| o1 | N.A. | 74.4 | 94.8 | 77.3 |
| Open Weights | ||||
| Qwen2.5-32B-Instruct | N.A. | 26.7 | 84.0 | 49.0 |
| r1 | $\gg$800K | 79.8 | 97.3 | 71.5 |
| Open Weights and Open Data | ||||
| s1 w/o BF | 1K | 50.0 | 92.6 | 56.6 |
| s1-32B | 1K | 56.7 | 93.0 | 59.6 |
- 数据筛选策略的重要性: 消融实验证明,本文提出的“质量+困难度+多样性”三合一数据筛选策略至关重要。仅依赖随机采样、仅最大化多样性或仅选择最长推理链的策略,性能均远差于s1K。同时,直接使用全部5.9万样本进行训练,虽然性能略有提升,但性价比远低于使用s1K。这再次印证了在推理微调中“精甚于多”的原则。
| 数据集 | AIME 2024 | MATH 500 | GPQA Diamond |
|---|---|---|---|
| 1K-random | 36.7 | 90.6 | 52.0 |
| 1K-diverse | 26.7 | 91.2 | 54.6 |
| 1K-longest | 33.3 | 90.4 | 59.6 |
| 59K-full | 53.3 | 92.8 | 58.1 |
| s1K | 50.0 | 93.0 | 57.6 |
- 预算强制方法的优越性: 在多种测试时扩展方法的比较中,预算强制在控制度、扩展性和最终性能上均表现最佳。其他方法,如通过prompt指令控制思考步数或token数,效果不佳且难以控制。
| 方法 | 控制度 | 扩展性 | 性能 |
|---|---|---|---|
| BF (预算强制) | 100% | 15 | 56.7 |
| TCC (token条件控制) | 40% | -24 | 40.0 |
| SCC (step条件控制) | 60% | 3 | 36.7 |
| RS (拒绝采样) | 100% | -35 | 40.0 |
最终结论
本文成功证明,构建一个高性能、可扩展的推理模型并不一定需要复杂的技术和海量的数据。通过在1000个精心挑选的样本上进行SFT,并结合简单的“预算强制”技术,即可激活预训练模型的强大推理潜能,并实现清晰的“测试时扩展”效果。这一简单、高效且完全开源的方案为未来推理模型的研究和应用提供了一个低成本、高回报的新范式。