Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters

ArXiv URL: http://arxiv.org/abs/2408.03314v1
作者: Aviral Kumar; Kelvin Xu; C. Snell; Jaehoon Lee
发布机构: Google DeepMind; University of California, Berkeley

TL;DR

本文提出了一种“计算最优”扩展策略，即根据问题的难度自适应地分配测试时（test-time）的计算资源，并证明在特定场景下，这种策略比单纯扩展模型参数能更有效地提升大型语言模型（LLM）的性能。

关键定义

本文沿用了领域内的一些关键定义，并提出了一个核心策略概念：

测试时计算 (Test-Time Computation): 指在模型部署后，针对一个具体输入（prompt），为了生成或改进输出而额外花费的计算资源。这与模型预训练或微调阶段的计算相对应。
提议者与验证者 (Proposer and Verifier): 本文将测试时计算方法统一为两个模块的交互。提议者负责生成候选答案（即修改提议分布），例如通过多次独立采样或迭代修正；验证者负责评估和筛选这些候选答案，例如使用结果导向的奖励模型（ORM）或过程导向的奖励模型（PRM）。
过程奖励模型 (Process Reward Model, PRM): 一种验证者，与评估最终答案的ORM不同，PRM能够对解决方案中的每一个中间步骤的正确性进行打分，从而为更精细的搜索算法提供指导。
计算最优扩展策略 (Compute-Optimal Scaling Strategy): 本文的核心概念。指对于给定的问题和计算预算，选择最优的超参数组合（如搜索算法、并行采样数 vs. 序列修正步数），以最大化模型输出的正确率。其形式化表示为：
\[\theta^*_{q,a^*(q)}(N)=\operatorname{argmax}_{\theta}\left( \mathbb{E}_{y\sim\operatorname{Target}(\theta,N,q)}\left[\mathbf{1}_{y=y^*(q)}\right]\right),\]
其中 $q$ 是输入问题，$y^*(q)$ 是正确答案，$N$ 是计算预算，$\theta$ 是测试时计算策略的超参数。
问题难度 (Question Difficulty): 实现“计算最优策略”的关键指标。本文不采用人工标签，而是根据一个基准模型在某个问题上的成功率（pass@1 rate）来定义其难度。通过将问题划分到不同的难度区间（bins），可以为每个区间选择最优的计算策略。

本文方法

本文提出了一个统一框架和一种“计算最优”的元策略，来有效扩展测试时计算。其核心思想是，测试时计算的效率取决于问题难度，因此应根据难度自适应地选择策略。

统一视角：提议者与验证者

本文将测试时计算方法分解为两个独立但可组合的维度：

优化提议分布 (Refining the Proposal Distribution): 改变生成答案的方式。本文的核心方法是迭代修正 (revisions)，即微调模型使其能够根据自己先前生成的错误答案进行迭代改进，从而在测试时通过序列化的修正来优化答案。
优化验证者 (Optimizing the Verifier): 改进答案的评估和筛选方式。本文的核心方法是使用过程奖励模型 (PRM)，并在此基础上执行不同的搜索算法 (search methods)，如 $best-of-N$、$beam search$ 和 $lookahead search$。

核心思想：基于难度的计算最优策略

本文发现，不同的计算策略在不同难度的问题上表现各异。例如，对于简单问题，模型初始答案可能方向正确但有小错，此时进行“迭代修正”更有效；对于困难问题，模型可能需要探索完全不同的解题思路，此时进行大规模的“并行采样和搜索”可能更佳。

基于此洞察，本文提出计算最优扩展策略：

评估难度：对于一个新问题，首先评估其对当前模型而言的“难度”。这通过一个轻量的评估过程（如用验证者对少量样本打分）来近似实现。
分配策略：根据评估出的难度等级，从预先在验证集上为每个难度等级选出的“最优”计算策略（如特定的搜索方法，或特定的并行/序列采样比例）中，选择对应的一种来解决当前问题。

在验证者维度上的应用：搜索

本文通过训练一个无需人工标注的PRM，对比了三种基于PRM的搜索方法：

Best-of-N weighted: 独立采样N个完整答案，然后由PRM评分，通过加权投票选出最终答案。
Beam search: 在生成答案的每一步，保留N个候选项，使用PRM评分并选择最好的M个进行下一步扩展。
Lookahead search: Beam search的加强版，在评估当前步骤时，会向前“模拟”生成k步，并使用模拟终点的PRM分数来评估当前步骤的优劣。

不同PRM搜索方法对比

图注：左：Best-of-N；中：Beam search；右：Lookahead search。

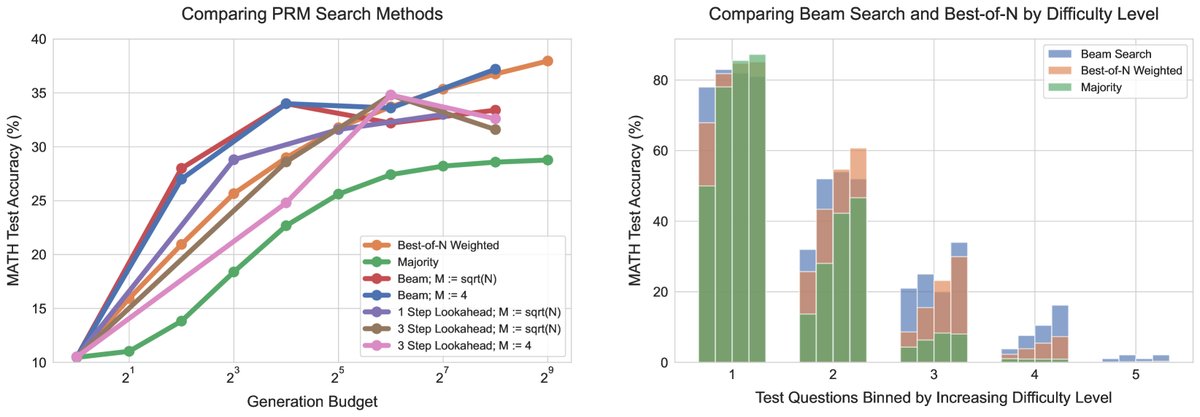
发现：

在低计算预算下，$Beam search$ 优于 $Best-of-N$。但随着预算增加，$Beam search$ 可能会过度利用PRM的弱点，导致性能下降。
$Beam search$ 在中等和较难问题上表现更好，而 $Best-of-N$ 在简单问题上更鲁棒。
通过应用计算最优策略（即根据问题难度在 $Best-of-N$ 和 $Beam search$ 中切换），其性能可以远超任何单一策略，用少至 $4x$ 的计算量就能达到 $Best-of-N$ 的效果。

计算最优搜索策略与基线的对比

图注：计算最优策略（橙色/蓝色曲线）在低计算预算下，仅用16个生成样本就能接近或超过Best-of-N基线在64个样本时的性能。

在提议者维度上的应用：修正

本文微调模型，使其具备迭代修正答案的能力。实验对比了两种资源分配方式：

并行采样 (Parallel sampling): 类似$Best-of-N$，一次性独立生成N个答案。
序列修正 (Sequential revisions): 生成一个答案，然后将其作为上下文，让模型生成一个修正版本，重复N次。

并行采样 vs. 序列修正

图注：并行采样与序列修正的流程图，以及两者结合的策略。

发现：

在总计算量相同的情况下，纯粹的序列修正略优于纯粹的并行采样。
最优策略是两者的结合。其最佳混合比例取决于问题难度：简单问题更适合纯序列修正（局部优化）；难题则需要一定比例的并行采样来保证探索（全局搜索）。
同样，通过应用计算最优策略，可以在测试时根据问题难度动态调整并行与序列的计算分配比例，从而达到最佳性能。

不同并行/序列比例对不同难度问题的影响

图注：右图显示，对于简单问题（bin 1, 2），完全采用序列修正（横轴最左端）性能最好；而对于难题（bin 3, 4, 5），则需要在并行和序列间找到一个平衡点。

创新点

本文的核心创新不在于提出一个全新的算法，而在于提出了一个元策略 (meta-strategy)：根据问题难度自适应地分配测试时计算资源。它首次系统性地分析并证明了，没有任何一种单一的测试时计算方法是普适最优的，最优策略是动态变化的。通过将此问题框架化为一个优化问题，并提供了一个基于“问题难度”的实用解法，本文显著提升了测试时计算的效率。

实验结论

主要结果总结

实验在MATH数学推理基准上进行，使用了PaLM 2-S*模型。

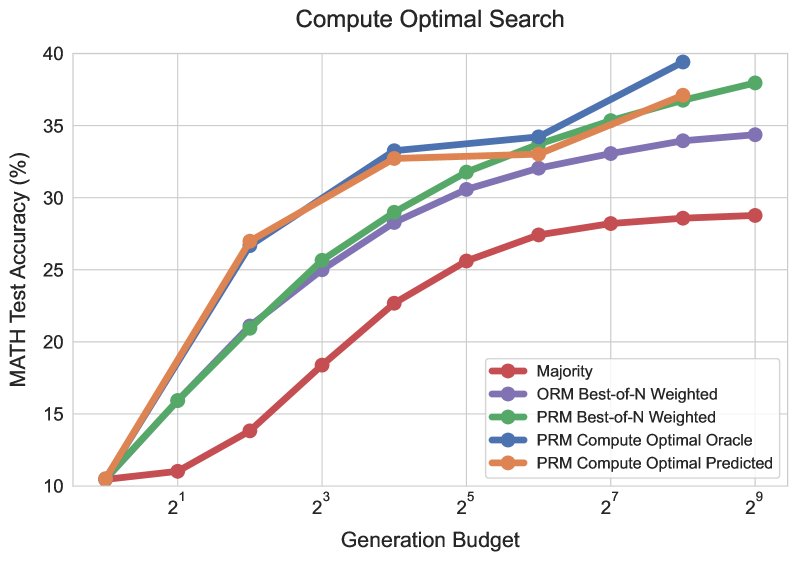
测试时计算效率显著提升：通过应用“计算最优”策略，无论是在PRM搜索还是迭代修正的场景下，都能以比 $Best-of-N$ 基线少 $4倍$ 的计算量达到甚至超越其性能。
测试时计算 vs. 模型参数扩展：在总计算量（预训练FLOPs + 推理FLOPs）匹配的情况下，一个较小的模型（PaLM 2-S*）配合“计算最优”的测试时计算策略，其性能可以超过一个比它大14倍的预训练模型。
方法的适用范围与局限性：
- 表现最佳的场景：对于中低难度的问题，即基础模型已经具备一定解决能力（pass@1不为零），测试时计算能非常有效地进行搜索或修正，从而找到正确答案。在这种场景下，增加测试时计算通常比扩展模型参数更具性价比。
- 表现不佳的场景：对于最困难的问题（如难度等级5），基础模型几乎完全无法产生有用的解题思路。此时，再多的测试时计算也难以“无中生有”，性能提升微乎其微。在这种情况下，通过扩展模型参数进行预训练仍然是提升性能更有效的方式。
最终结论：本文的结论是，扩展测试时计算是一种可行且高效的性能提升路径，尤其是在模型的“推理能力”而非“知识储备”成为瓶颈时。这暗示了未来的一种可能性：与其投入海量资源预训练更大的模型，不如训练一个“足够好”的中等大小模型，然后在推理时根据任务难度智能地投入更多计算资源来解决问题。