Scaling up Multi-Turn Off-Policy RL and Multi-Agent Tree Search for LLM Step-Provers

• ArXiv URL: http://arxiv.org/abs/2509.06493v1

• 作者: Zeyu Zheng; Ran Xin; Xia Xiao; Kun Yuan

• 发布机构: ByteDance; Carnegie Mellon University; Peking University

---

TL;DR

本文介绍了BFS-Prover-V2，一个通过创新的训练与推理扩展技术来提升大型语言模型（LLM）定理证明能力的系统，它结合了克服性能瓶颈的多阶段强化学习框架和用于分层推理的规划器增强型多智能体搜索架构，从而在多个数学基准测试中取得了当前最优性能。

关键定义

本文提出或沿用了以下对理解至关重要的核心概念：

• 马尔可夫决策过程 (Markov Decision Process, MDP) 公式化: 本文将交互式定理证明建模为一个MDP。其中，状态 (State) 是Lean编译器的当前策略状态（包含已知假设和待证目标），动作 (Action) 是LLM生成的策略字符串，转移 (Transition) 由Lean编译器确定性地执行，奖励 (Reward) 则对成功证明路径上的每一步给予+1，其余为0。
• 多阶段专家迭代 (Multi-stage Expert Iteration): 一种受AlphaZero启发的离策略 (off-policy) 强化学习框架。它包含一个内循环，通过“证明生成”和“模型优化”交替进行来积累经验；同时包含一个外循环，通过周期性重训练来帮助模型跳出局部最优，实现长期性能增长。
• 自适应策略过滤 (Adaptive Tactic Filtering): 一种在训练时使用的动态数据筛选策略。它根据模型对生成策略的困惑度（Perplexity）来筛选训练数据，仅保留那些既非过于简单（低困惑度）也非充满噪声或过于复杂（高困惑度）的“恰到好处”的策略，形成一种自动化的课程学习机制。
• 规划器-证明器范式 (Planner-Prover Paradigm): 一种用于推理的分层架构。它由一个高层规划器 (Planner) 和一个底层证明器 (Prover) 组成。规划器负责将复杂定理分解为一系列更简单的子目标（引理），而证明器则专注于解决这些具体的子目标。

相关工作

当前，将大型语言模型（LLM）与交互式定理证明器（如Lean4）相结合已成为神经符号AI系统的前沿方向。其核心反馈循环为：LLM提出证明步骤（策略），编译器进行严格验证，强化学习（RL）利用验证结果持续优化LLM的推理能力。

然而，该领域面临两大相互关联的扩展性挑战：

1. 训练时扩展瓶颈: 在应用强化学习训练LLM时，模型性能在初期快速提升后，普遍会遭遇“性能平台期”，即使用持续的训练也难以进一步提升，这限制了模型掌握更复杂问题的能力。
2. 推理时扩展瓶颈: 现实中的数学问题往往需要深度、多步的推理，并探索指数级增长的搜索空间。即使拥有强大的基础模型，若无高效的搜索策略，模型也会被组合爆炸的复杂性所淹没。

本文旨在解决上述双重扩展性问题，提出一套完整的训练和推理系统，以实现LLM证明器能力的持续提升和对复杂问题的高效求解。

本文方法

BFS-Prover-V2系统从训练和推理两个维度着手，以解决LLM证明器面临的扩展性挑战。其方法建立在将定理证明形式化为马尔可夫决策过程（MDP）的基础之上。

训练时扩展：多阶段专家迭代

为了克服训练中的性能平台期，本文设计了一个精巧的、基于专家迭代的离策略强化学习流程，实现了能力的持续增长。

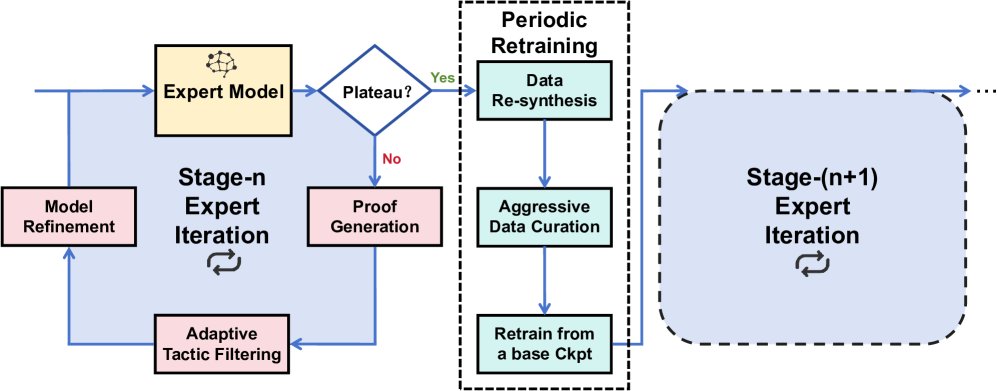
图1：训练时扩展架构总览。系统首先评估当前专家模型的性能。若性能仍在提升，则进入内层专家迭代循环（生成证明、自适应策略过滤、模型优化）。若性能停滞，则触发外层重训练循环（数据再合成、激进数据筛选、从头重训练模型），产生一个性能更强的新专家模型。

创新点1：自适应策略过滤

在专家迭代的“模型优化”阶段，并非所有成功证明中的策略（tactic）都有同等的学习价值。本文提出了一种基于策略困惑度（Perplexity）的自适应过滤方法，实现了自动化的课程学习。

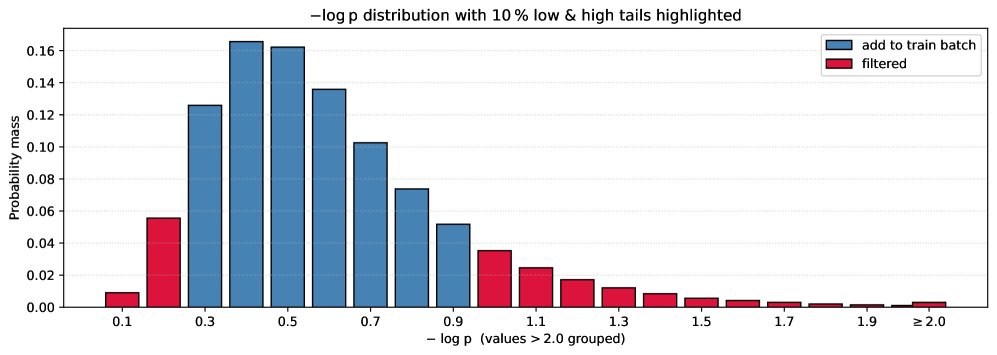
图2：基于困惑度分布的策略级数据过滤。该图展示了一轮专家迭代中策略困惑度的分布。系统过滤掉两端的数据（红色部分）：低困惑度部分代表模型已熟练掌握的简单步骤；高困惑度部分往往是充满噪声或不必要地复杂的策略。仅使用中间分布（蓝色部分）的数据进行训练，能让模型专注于学习有挑战性且有意义的示例。

该方法将数据分为三类：

• 低困惑度尾部: 模型已高度自信的简单步骤。训练这些数据几乎没有收益，反而可能导致过拟合。
• 高困惑度尾部: 模型认为“惊奇”的步骤。研究发现这通常不是巧妙的推理，而是噪声或次优选择（例如，用一个复杂通用策略解决一个简单问题）。训练这些数据可能导致模型产生“幻觉”，降低核心推理能力。
• 中心分布区: 这是“恰到好处”的学习区域。这些策略对当前模型有挑战性，但仍在可理解的范围内。

通过仅保留中心区域的数据进行训练，确保模型始终在其“最近发展区”内学习，从而实现稳定、持续的性能提升。

创新点2：周期性重训练

即便有自适应过滤，模型在多轮迭代后仍可能陷入局部最优，形成固化的证明“风格”，无法发现解决新难题所需的新方法。为此，本文引入了周期性的“软重置”机制。

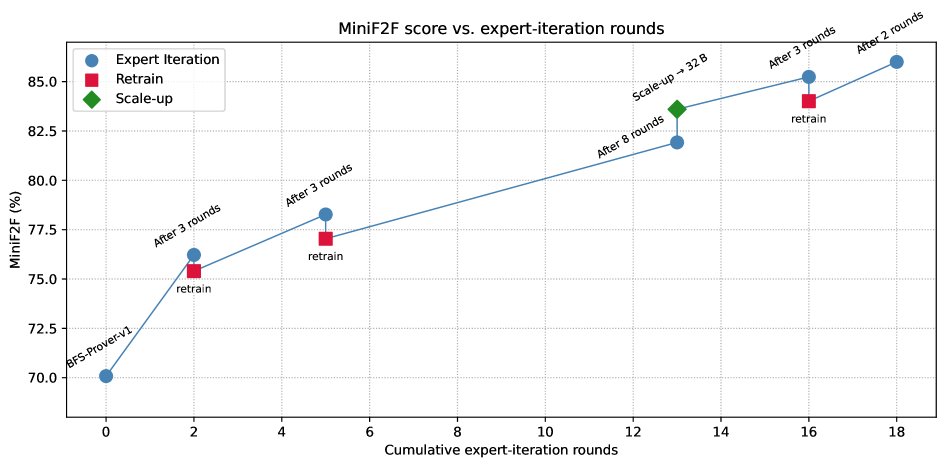
图3：通过专家迭代和周期性重训练实现持续性能提升。图中蓝点表示证明器在MiniF2F基准上的性能随专家迭代轮数稳步增长，但最终趋于平稳。为打破瓶颈，系统周期性地进行“软重置”（红方块），即用当前最优模型重新生成更优的训练数据，并从基础检查点重新训练模型。此举能帮助模型跳出局部最优，实现性能的阶梯式跃升。图中绿菱形展示了模型规模扩大至32B参数后的效果。

该过程包括三个步骤：

1. 数据再合成与去噪: 使用当前最强的证明器，重新解决过去所有遇到过的问题。由于能力更强，它能找到更简洁、更优雅的证明，从而生成一个更高质量的“去噪”版数据集。
2. 激进数据筛选: 对新生成的高质量数据应用更严格的困惑度过滤，仅保留最核心、信息量最大的策略步骤。
3. 从基础检查点重训练: 用这个小而精的数据集完全替换旧数据，并从一个通用的预训练检查点重新开始训练模型。

这个过程虽然会带来暂时的性能下降，但新模型具备了更强的探索潜力，能发现以往模型无法企及的证明路径，最终突破原有的性能天花板。

推理时扩展：规划器增强的多智能体搜索

对于复杂的数学定理，仅靠强大的模型本身是不够的。本文为此设计了一套分层推理架构，模拟人类数学家先规划蓝图再填充细节的思考方式。

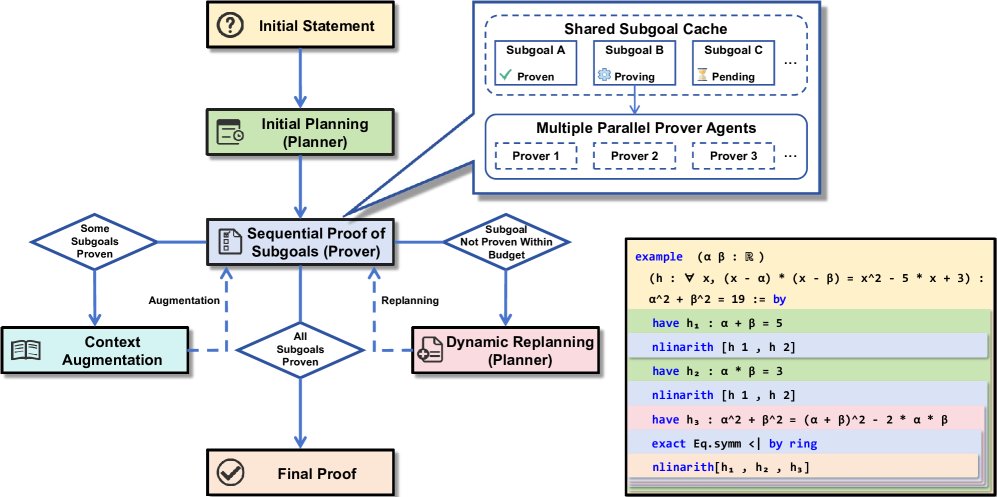
图4：规划器增强的多智能体树搜索架构总览。规划器智能体将主定理分解为一系列子目标，这些子目标由一个共享的子目标缓存管理，并由多个证明器智能体并行解决。成功证明的子目标会增强主证明的上下文，而失败则可能触发动态重规划循环。插图展示了一个玩具示例，说明证明中间引理（h1, h2, h3）如何促进最终目标的证明。

创新点3：规划器-证明器范式

该架构将证明任务分工给两类智能体：

• 规划器 (Planner): 一个通用的高层推理LLM，负责战略分解。它不生成具体策略，而是提出一系列关键的中间子目标（引理）。这个过程将一个庞大、难解的搜索问题，转化为一连串更小、更易处理的问题。
• 证明器 (Prover): 经过多阶段专家迭代训练的专用LLM，负责执行。它一次接收一个子目标，并结合最佳优先搜索（BFS）来寻找该子目标的具体证明步骤。

优点：动态与协作

该系统通过一个动态循环来运作，并利用多智能体协作来加速。

• 动态重规划 (Dynamic Replanning): 如果证明器在一定计算预算内未能解决某个子目标，系统不会终止。相反，它会再次查询规划器，但这次的输入包含了所有已成功证明的子目标。规划器基于更新后的上下文生成一个修正后的新计划，使得系统对“卡住”的情况具有鲁棒性。
• 聚焦并行与共享缓存 (Focused Parallelism & Shared Cache): 系统部署多个证明器实例，但它们并非分头解决不同子目标，而是集中所有算力共同解决当前的一个子目标。这能快速攻克难点。所有智能体通过一个共享子目标缓存 (Shared Subgoal Cache)进行通信，一旦有任何一个智能体找到解法，它会立即将结果写入缓存，并通知所有其他智能体停止搜索，从而避免了重复计算，并集体转向下一个子目标。

实验结论

• 模型与数据: 证明器智能体基于Qwen2.5-Math-7B/32B模型进行优化，规划器采用Gemini2.5-pro。训练语料库通过自动形式化技术构建，包含了约300万个数学问题。
• 关键实验结果: BFS-Prover-V2在两个关键基准测试中取得了当前步骤级证明器的最佳性能：
  • 在MiniF2F测试集上达到 95.08% 的通过率。
  • 在ProofNet测试集上达到 41.4% 的通过率。
• 结果分析:
  • 在MiniF2F上接近饱和的性能，验证了本文提出的多阶段强化学习流程能够有效掌握一个给定的问题分布。
  • 在ProofNet上的强劲表现则更具意义，它表明系统具备良好的泛化能力，能够将其从高中竞赛级问题中学到的知识，成功迁移到更复杂、依赖大型数学库的本科级别问题上。
• 最终结论: 本文提出的双重扩展策略是成功的。训练时的多阶段专家迭代（包含自适应过滤和周期性重训练）有效克服了性能平台期，实现了模型的持续进步。推理时的规划器-证明器分层架构，则使系统能够有效应对复杂定理的巨大搜索空间。这些方法的结合，共同将LLM步骤级证明器的能力推向了新的高度。

下表将BFS-Prover-V2与其他顶尖的定理证明器进行了比较。

证明器方法	预算	miniF2F-test	miniF2F-valid	ProofNet-test
步骤级证明器
InternLM2.5-StepProver-7B [32]	256 × 32 × 600	65.9%	69.6%	≈ 27%
Hunyuan-Prover-7B [14]	600 × 8 × 400	68.4%	-	-
BFS-Prover-V1-7B [36]	2048 × 2 × 600	70.8%	-	-
	累积	73.0%	-	-
MPS-Prover-7B† [15]	64 × 4 × 800 × 8	72.54%	-	-
	累积	75.8%	-	-
BFS-Prover-V2-7B (本文)	累积	82.4%	-	-
BFS-Prover-V2-32B (本文)	累积	86.1%	85.5%	41.4%
使用规划器	累积	95.1%	95.5%	-
完整证明生成器
DeepSeek-Prover-V2-671B [23]	8192	88.9%	90.6%	37.1%
Kimina-Prover-72B† [30]	1024	87.7%	-	-
w/ TTRL 搜索	累积	92.2%	-	-
Goedel-Prover-32B† [17]	8192	92.2%	-	-
w/ 自我修正	1024	92.6%	-	-
Delta-Prover† [43]	累积	95.9%	-	-
Seed-Prover† [6]	累积	99.6%	-	-

表1：BFS-Prover-V2与其他领先的定理证明器性能对比。†表示同期工作。