Seesaw: Accelerating Training by Balancing Learning Rate and Batch Size Scheduling
-
ArXiv URL: http://arxiv.org/abs/2510.14717v1
-
作者: Cengiz Pehlevan; Costin-Andrei Oncescu; Depen Morwani; Jingfeng Wu; Alexandru Meterez
-
发布机构: Harvard University; University of California, Berkeley
TL;DR
本文提出了一种名为 Seesaw 的训练加速方法，它通过将标准学习率调度中的衰减部分转化为批次大小（batch size）的增加，从而在保持模型性能（以 FLOPs 衡量）的同时，显著减少了约 36% 的训练墙钟时间。
关键定义
- Seesaw: 本文提出的核心调度算法。其原理是，当一个标准的学习率调度器（如余弦退火）需要将学习率乘以因子 $\alpha$ ($\alpha < 1$) 时，Seesaw 将学习率乘以 $\sqrt{\alpha}$，同时将批次大小（batch size）扩大 $1/\alpha$ 倍。这种转换旨在保持损失动态不变，同时通过增大批次来减少所需的串行训练步数。
- 临界批次大小 (Critical Batch Size, CBS): 在训练中，超过这个批次大小后，进一步增大批次会降低样本效率（即每处理一个样本带来的模型提升减少），从而限制了训练速度的提升。Seesaw 方法主要在临界批次大小之内有效。
- 归一化随机梯度下降 (Normalized SGD, NSGD): Adam 优化器的一个简化分析代理。其更新规则为 $\theta_{t} = \theta_{t} - \eta \frac_{t}}{\sqrt{\mathbb{E}\ \mid {\mathbf{g}}_{t}\ \mid ^{2}}}$。本文利用 NSGD 来为 Adam 这类自适应优化器建立学习率与批次大小关系的理论基础。
- 方差主导机制 (Variance-dominated regime): 本文理论分析的一个核心假设，即在 NSGD 的更新规则中，分母项（梯度的期望平方范数 $\mathbb{E}\ \mid {\mathbf{g}}_{t}\ \mid ^{2}$）主要由梯度噪声的方差决定，而非梯度的均值。这个方差项与批次大小成反比，因此该假设在批次大小未超过临界批次大小时通常成立。
相关工作
当前，大规模语言模型（LLM）的训练通常依赖于巨大的计算资源和漫长的训练时间。一个普遍用于减少墙钟时间的策略是增大训练的批次大小，以利用数据并行带来的加速。然而，当批次大小超过一个“临界批次大小”（CBS）后，单纯增加批次会损害模型的收敛效率。
尽管业界已经在使用“批次渐增”（batch ramp，即在训练过程中逐渐增大学习率）的策略（如 LLaMA、OLMo），但这些方法大多是基于经验的启发式调整，缺乏坚实的理论基础。特别是对于 Adam 这类自适应优化器，学习率衰减和批次大小增加之间的最优权衡关系尚不明确。
本文旨在解决这一问题：为批次大小调度提供一个有原则的、理论驱动的框架，从而系统性地利用批次大小的增加来加速训练，而不仅仅依赖于启发式调整。
本文方法
本文提出的 Seesaw 方法，其核心思想是建立学习率衰减和批次大小增加之间的等效关系，从而将原本的学习率衰减操作替换为批次大小的增加，以减少总训练步数。
从 SGD 到 NSGD 的理论推导
首先，方法从简单的随机梯度下降（SGD）入手。直观上，对于 SGD，进行 2 次步长为 $\eta/2$、批次为 $B$ 的更新，其效果（在一阶泰勒展开下）约等于进行 1 次步长为 $\eta$、批次为 $2B$ 的更新。这表明在 SGD 中，学习率和批次大小大致遵循线性反比关系。
然而，对于自适应优化器 Adam，关系更为复杂。为了进行理论分析，本文使用归一化随机梯度下降（NSGD）作为 Adam 的一个可分析的代理。Adam 的更新规则如下：
\[\begin{aligned} {\mathbf{m}}_{t} &= \beta_{1}{\mathbf{m}}_{t-1} + (1-\beta_{1}){\mathbf{g}}_{t} \\ {\mathbf{v}}_{t} &= \beta_{2}{\mathbf{v}}_{t-1} + (1-\beta_{2}){\mathbf{g}}_{t}^{2} \\ \theta_{t} &= \theta_{t} - \eta\frac{{\mathbf{m}}_{t}}{\sqrt{{\mathbf{v}}_{t}}+{\epsilon}} \end{aligned}\]通过简化（设置 $\beta_1=\beta_2=0$ 并使用标量预处理器），可以得到 NSGD 的更新规则：
\[\theta_{t} = \theta_{t} - \eta\frac{{\mathbf{g}}_{t}}{\sqrt{\mathbb{E}\ \mid {\mathbf{g}}_{t}\ \mid ^{2}}}\]创新点
本文的核心创新在于，在“方差主导”的假设下，为 NSGD (以及 Adam) 建立了新的学习率-批次大小等效关系。
该假设认为，更新规则的分母 $\mathbb{E}\ \mid {\mathbf{g}}_{t}\ \mid ^{2}$ 主要由与批次大小成反比的方差项贡献。即 $\mathbb{E}\ \mid {\mathbf{g}}_{t}\ \mid ^{2} \approx \text{variance} \propto 1/B$。在此条件下，NSGD 的更新步长近似于 $\eta \frac_{t}}{\sqrt{C/B}} \propto (\eta\sqrt{B}) {\mathbf{g}}_{t}$。这表明有效学习率与 $\eta\sqrt{B}$ 成正比。
为了保持训练动态不变，必须维持 $\eta\sqrt{B}$ 为常数。因此，如果一个标准调度器将学习率从 $\eta$ 降低到 $\eta’ = \eta / \alpha_c$，为了找到一个等效的批次大小 $B’$，需要满足 $\eta\sqrt{B} = (\eta/\alpha_c) \sqrt{B’}$，解得 $B’ = B \cdot \alpha_c^2$。
Seesaw 算法利用了这一关系：当标准调度器（如余弦退火）计划将学习率降低一个因子 $\alpha$ 时，Seesaw 将此操作替换为：
- 学习率降低一个较小的因子 $\sqrt{\alpha}$。
- 批次大小增加一个因子 $\alpha$。
这个组合保持了理论上的等效性（$\text{新的学习率衰减因子} \times \sqrt{\text{新的批次大小增加因子}} = \sqrt{\alpha} \times \sqrt{\alpha} = \alpha = \text{原学习率衰减因子} \times \sqrt{1}$），但通过增加批次大小减少了总训练步数。
Seesaw 伪代码: ``$$ 输入: η_0 (初始学习率), B_0 (初始批次大小), α > 1 (步阶衰减因子), S (调度器降低 η 的步数集合), T (总训练步数)
η ← η_0, B ← B_0 for t = 1 to T: if t ∈ S: η ← η / √α; // 学习率减小 B ← B * α; // 批次大小增加 end if // … 执行一步训练 … end for $$``
优点
- 理论驱动：与启发式方法不同，Seesaw 基于对 NSGD 动态的分析，为自适应优化器下的批次调度提供了理论依据。
- 显著加速：通过将学习率衰减转换为批次大小增加，Seesaw 能在不牺牲模型性能的前提下，将墙钟训练时间减少约 36%（对于余弦衰减），接近理论极限。
- 即插即用：Seesaw 可作为现有学习率调度器（如余弦退火）的直接替代品，易于集成到现有训练流程中。
此外，理论分析还推导出一个稳定性约束：$\alpha_{\text{衰减}} \geq \sqrt{\beta_{\text{增加}}}$。Seesaw 采用的策略（$\sqrt{\alpha}, \alpha$）正好位于这个约束的边界上，是理论上最激进且稳定的选择。
实验结论
本文通过在 150M、300M 和 600M 参数规模的模型上进行实验，验证了 Seesaw 方法的有效性。所有模型均在 Chinchilla 规模（即数据量 $D=20N$）下进行预训练。
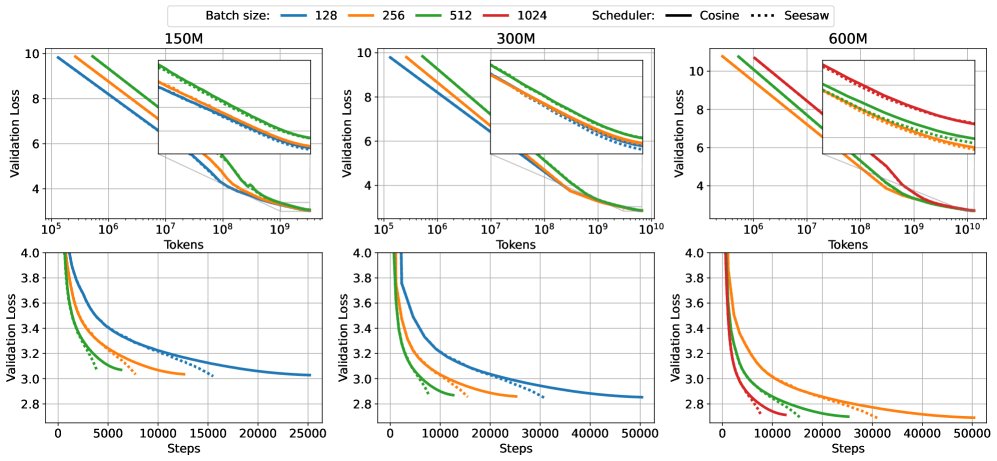上图展示了在不同模型规模下，Seesaw（橙色/绿色）与标准余弦退火（蓝色）的对比。上排（FLOPs vs Loss）显示两者性能相当，下排（Wall Time vs Loss）显示 Seesaw 显著节省了时间。
关键实验结果总结：
- 性能匹配，时间缩短：实验表明，在临界批次大小（CBS）内，Seesaw 能够匹配标准余弦退火调度器的最终验证损失（见下表），同时将墙钟训练时间减少约 36%。这证实了 Seesaw 在不牺牲模型性能的前提下实现了显著的训练加速。
| 模型规模 | B=128 | B=256 | B=512 | B=1024 |
|---|---|---|---|---|
| 150M (cosine) | 3.0282 | 3.0353 | 3.0696 | 3.1214 |
| 150M (Seesaw) | 3.0208 | 3.0346 | 3.0687 | 3.1318 |
| 300M (cosine) | 2.8531 | 2.8591 | 2.8696 | 2.9369 |
| 300M (Seesaw) | 2.8452 | 2.8561 | 2.8700 | 2.9490 |
| 600M (cosine) | - | 2.6904 | 2.6988 | 2.7128 |
| 600M (Seesaw) | - | 2.6883 | 2.6944 | 2.7132 |
最终验证损失对比，Seesaw 与余弦退火在不同批次大小下表现相当。
- 理论约束验证：实验验证了理论推导出的最激进调度策略。如下图所示，当调度策略违反稳定性约束（$\alpha < \sqrt{\beta}$，如图中红色和紫色线）时，模型性能会下降；而 Seesaw 采用的边界策略（绿色线）则能很好地匹配基线（蓝色线）。
在150M模型上的实验，验证了理论约束的有效性。过于激进的批次增加策略（红、紫）导致性能下降。
- 方法的局限性：当训练的批次大小远超 CBS 时，Seesaw 的优势消失，性能甚至劣于标准余弦退火。如下图所示，在非常大的批次下，Seesaw（绿色）无法匹配基线（蓝色）。这是因为此时“方差主导”的假设不再成立，梯度中的噪声很小，学习率的衰减变得不可或缺，无法再被批次大小的增加所替代。
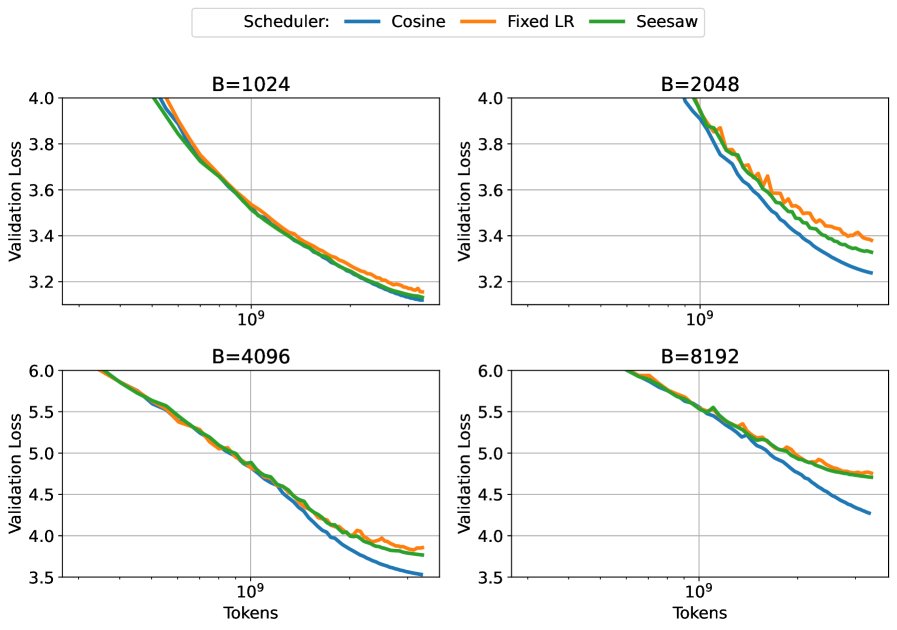在远超CBS的大批次下，Seesaw（绿色）及其他变体都无法匹配基线性能（蓝色）。
总结
本文成功地为 LLM 训练中的批次大小调度提供了理论基础，并基于此设计了 Seesaw 算法。实验证明，Seesaw 是一个简单而有效的即插即用方案，可在不影响模型最终性能的情况下，显著加快训练速度。其核心贡献在于揭示了在自适应优化器下（特定条件下），学习率衰减与批次大小增加之间的 $\eta \sqrt{B}$ 等效关系，并将其转化为一个实用的加速工具。不过，该方法的有效性主要局限于临界批次大小以内的训练场景。