SFT Doesn’t Always Hurt General Capabilities: Revisiting Domain-Specific Fine-Tuning in LLMs

• ArXiv URL: http://arxiv.org/abs/2509.20758v1

• 作者: Tian Wang; Dakuo Wang; Weiqi Zhang; Hansi Zeng; Ruochen Jiao; Zhongruo Wang; Hyokun Yun; Kai Zhong; Arvind Srinivasan; Kun Qian; 等15人

• 发布机构: Amazon; Northeastern University; University at Buffalo; University of Illinois Urbana-Champaign; University of Massachusetts Amherst; University of Texas at Austin

---

TL;DR

本文挑战了领域特定监督微调（SFT）必然损害大语言模型（LLM）通用能力的普遍观念，指出使用小学习率可以显著缓解性能下降，并提出了一种名为“令牌自适应损失重加权”（TALR）的新方法，以更有效地平衡领域知识注入与通用能力保持。

关键定义

本文沿用了现有研究中的核心概念，并为理论分析引入了新的形式化定义：

• 领域特定微调 (Domain-Specific Fine-Tuning - SFT)：使用特定领域（如医疗、电商）的数据集对预训练好的通用大语言模型进行额外训练，以增强其在该领域的专业能力。
• 通用能力下降 (General Capability Degradation)：指 LLM 在经过领域特定 SFT 后，其在通用基准（如数学推理、代码生成、指令遵循）上的性能出现下降的现象。
• 令牌自适应损失重加权 (Token-Adaptive Loss Reweighting - TALR)：本文提出的新方法。它通过一个带约束的优化问题，为序列中的每个令牌（token）计算一个自适应的损失权重。权重与模型对该令牌的预测概率成正比（\(w_i ∝ p_θ(x_i)^(1/τ)\)），从而在训练中自动降低“难令牌”（低概率令牌）的损失贡献，以减轻其对通用能力的负面影响。
• 令牌树 (Token Tree)：为理论分析引入的结构。一个深度为 \(n\) 的树，其中每个节点代表一个令牌，从根到叶节点的路径构成一个长度为 \(n\) 的令牌序列。用于形式化 LLM 的生成过程。
• LLM 压缩协议 (LLM Compression Protocol)：一种理论视角，将 LLM 视为数据压缩器。LLM 使用算术编码根据其预测的概率分布来编码令牌序列，训练效果通过编码长度的变化来衡量。

相关工作

当前，为了让 LLM 适应特定领域，监督微调（SFT）是标准做法。然而，大量研究表明，这种微调常常导致模型在数学、代码等通用任务上的“灾难性遗忘”（catastrophic forgetting），即通用能力显著下降。

领域内的主流研究可归入持续学习（continual learning）的范畴，特别是数据遗忘（data-oblivious）方法，即在不访问原始预训练数据的情况下保留已有知识。现有策略包括：

• 正则化方法：如 L2 正则化，通过惩罚参数的大幅变动来限制模型偏离初始状态。
• 模型平均：如 Wise-FT，通过加权平均预训练模型和微调后模型的参数来寻求平衡。
• 参数高效微调：如 LoRA，通过低秩更新限制参数修改的范围，从而减少对原始能力的破坏。
• 数据重加权：如 FLOW，通过调整难易样本的损失权重来缓解遗忘。

然而，这些方法大多直接借鉴自传统模型，对 LLM 独特的动态特性理解不足。此外，先前研究普遍在较大的学习率下得出“SFT 严重损害通用能力”的结论。

本文旨在解决的核心问题是：领域特定 SFT 是否必然导致严重的通用能力下降？以及如何设计更有效的策略来平衡领域适应和通用能力保持？

本文方法

学习率的关键作用

本文首先通过实验挑战了一个普遍认知。研究发现，通用能力的下降程度与学习率密切相关。

• 核心发现：使用一个非常小的学习率（如 \($1\mathrm{e}{-6}\)$），可以在显著减轻通用能力下降的同时，获得与使用大学习率（如 \($5\mathrm{e}{-6}\) 或 \($2\mathrm{e}{-5}\)$）相当的领域内任务性能。这表明许多先前研究中观察到的严重性能下降，部分原因可能是由于优化过程过于激进。

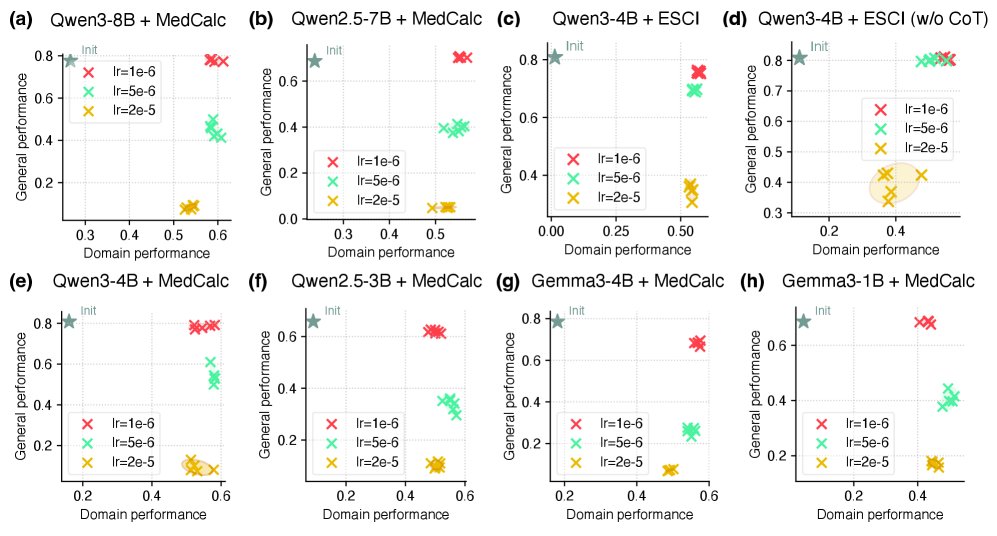
上图展示了在不同数据集和任务上，学习率对性能权衡的影响。散点图的右上角代表理想状态（领域性能和通用性能双高）。可以清晰地看到，较小的学习率（如 \($1\mathrm{e}{-6}\)$）对应的点普遍更靠近右上角，实现了更优的权衡。

理论分析

为了解释学习率的关键作用，本文从信息论角度提供了一套理论分析，将 LLM 视为一个数据压缩器，性能变化等同于编码长度的变化。

• 定理一（非正式表述）：通用能力的下降（即在通用数据上编码长度的增加）存在一个上界，这个上界与一个名为 \(λ\) 的分布更新步长成正比。在实践中，更小的学习率对应更小的 \(λ\)。因此，降低学习率可以收紧通用能力下降的上界，从而在理论上解释了小学习率能够缓解性能衰退的现象。
• 定理二（非正式表述）：在训练数据中，“难令牌”（即模型预测概率低的令牌）的数量越少，模型能够容忍的、不导致严重性能下降的安全学习率范围就越大。这解释了为什么在只预测最终标签（label-only）的微调任务中（相比于包含复杂推理过程的 CoT 任务，难令牌更少），即使用稍大的学习率（如 \($5\mathrm{e}{-6}\)$）也能取得不错的权衡效果。

理论分析进一步指出，通用能力下降的上界主要受“难令牌”（Hard Tokens）的更新幅度 \($M\_h\)$ 影响。因此，一个自然的想法是：减小难令牌在训练中的影响。

令牌自适应损失重加权 (TALR)

基于上述理论洞察，本文提出了 TALR 方法，旨在通过自适应地调整损失权重来抑制“难令牌”的过度影响。

创新点

传统方法需要手动设置阈值来区分难易令牌，而 TALR 提供了一种 principled（有原则的）、自适应的解决方案。它将权重计算构建为一个带约束的优化问题：

\[\min_{\mathbf{w}\in\Delta_{n}}\sum_{i=1}^{n}w_{i}\cdot\ell_{i}(\theta)+\tau\sum_{i=1}^{n}w_{i}\log w_{i}\]

该问题的目标是最小化加权损失，同时通过熵正则化项（\(τΣw_i log w_i\)）防止权重过度集中在少数令牌上。该优化问题有闭式解：

\[w_{i}^{*} \propto p_{\theta}(x_{i})^{1/\tau}\]

其中 \($w\_i^\*\)$ 是令牌 \($i\)$ 的最优权重，\($p\_{\theta}(x\_{i})\)$ 是模型预测该令牌的概率，\($τ\)$ 是控制权重平滑度的超参数。

优点

• 自适应性：权重与模型当前的预测概率直接相关。模型越不自信的令牌（概率低），其损失权重就越小。
• 动态性：在每个训练步，权重都会根据模型最新的预测重新计算，动态适应模型的学习进程。
• 无需手动调参：避免了为“难令牌”定义固定阈值或缩放因子的麻烦。

通过这种方式，TALR 在学习新领域知识的同时，温和地处理那些可能对模型已有通用知识造成剧烈冲击的“难令牌”，从而实现更好的平衡。

实验结论

关键结果

• 小学习率是强大的基线：实验证明，在领域特定 SFT 中，简单地将学习率调低（如 \($1\mathrm{e}{-6}\)$），本身就是一种非常有效的策略，可以大幅缓解通用能力的下降，其效果甚至优于一些复杂的缓解方法。

• TALR 的优越性：

  • 在小学习率下，TALR 表现出轻微优势，能够稳定地获得比其他方法（L2 正则化、LoRA、Wise-FT、FLOW）更好的性能权衡。
  • 在大学习率下，通用能力下降问题加剧，此时 TALR 的优势变得非常明显。它能在保持有竞争力的领域性能的同时，比所有基线方法更有效地减缓通用能力的损失。

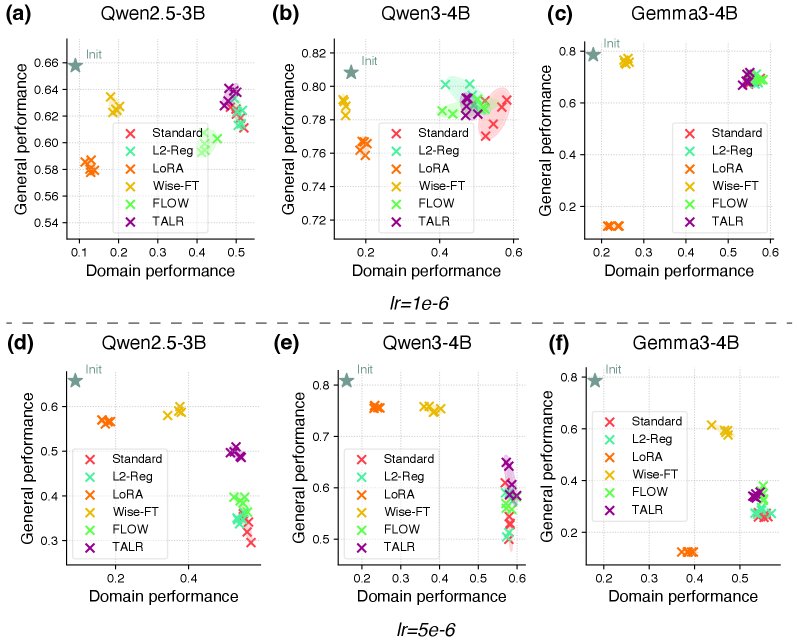
如上图所示，在学习率为 \($1\mathrm{e}{-6}\)$ 时（左侧图），大多数方法效果接近；但在 \($5\mathrm{e}{-6}\)$ 时（右侧图），TALR（橙色点）明显位于其他方法的右上方，实现了更优的权衡。

• 权衡依然存在：尽管 TALR 表现出色，但实验同样表明，没有任何一种现有方法能够完全消除领域适应和通用能力保持之间的权衡，尤其是在采用激进的大学习率时。

令牌级分析

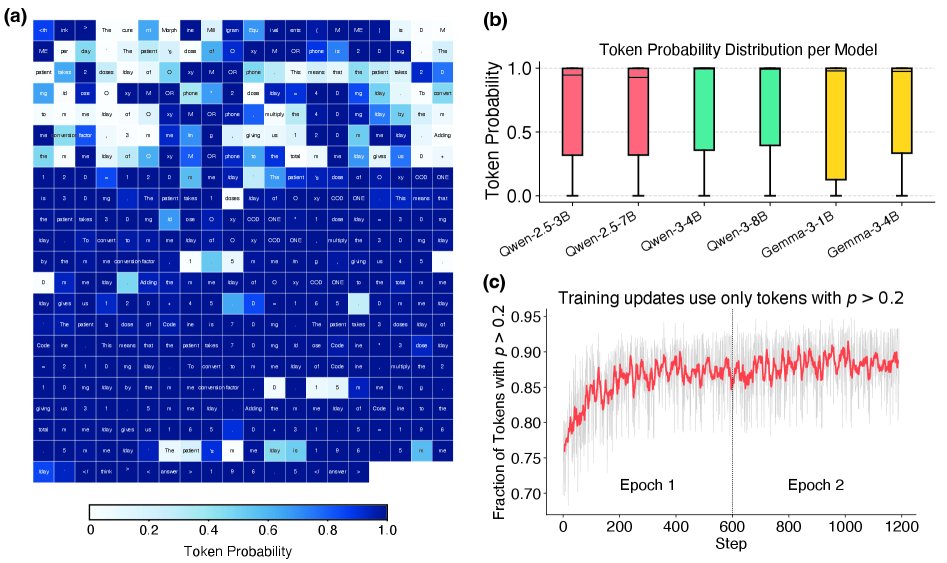
• 难令牌是关键：分析发现，训练数据中的大部分令牌对于预训练模型来说是“容易的”（预测概率高）。性能瓶颈来自于少数“难令牌”，这些令牌通常与预训练数据中覆盖不足的领域特定概念或知识相关。
• 隐式课程学习：TALR 在训练中会隐式地形成一种课程学习（Curriculum Learning）机制。在训练初期，模型更关注已经掌握得比较好的“容易”令牌；随着训练的进行，模型能力增强，原先的“难”令牌变得相对容易，其权重也随之增加，从而被逐步纳入学习范围。

总结

本文的核心结论是，领域 SFT 对通用能力的损害并非不可避免，其严重程度被先前研究高估。最终，本文提炼出两条实用的指导方针：

1. 首选策略：在进行领域特定 SFT 时，应首先尝试使用一个小的学习率。这通常能以最小的代价实现良好的性能权衡。
2. 进阶策略：如果需要进一步平衡领域性能和通用能力，或必须在较大学习率下训练，采用 TALR 是一种有效且稳健的选择。