Sigmoid Loss for Language Image Pre-Training

• ArXiv URL: http://arxiv.org/abs/2303.15343v4

• 作者: Alexander Kolesnikov; Xiaohua Zhai; Lucas Beyer; Basil Mustafa

• 发布机构: Google DeepMind

---

TL;DR

本文提出了一种用于语言-图像预训练的简单成对 Sigmoid 损失函数 (Sigmoid loss)，它将对比学习任务转化为对图文对的独立二元分类，从而解耦了损失计算与批次大小 (batch size) 的依赖，实现了更高的内存效率和在小批量数据下更优的性能。

关键定义

• Sigmoid Loss: 本文提出的核心损失函数。与在整个批次上进行归一化的传统 Softmax 对比损失不同，Sigmoid 损失将每个图文对 \((image, text)\) 视为一个独立的二元分类问题。对于匹配的正样本对，其标签为 \(+1\)；对于不匹配的负样本对，其标签为 \(-1\)。损失函数的目标是正确地对这些配对进行分类。
• SigLIP (Sigmoid Language Image Pre-training): 将本文提出的 Sigmoid 损失应用于从零开始训练语言-图像模型的框架，类似于 CLIP。
• SigLiT (Sigmoid Locked-image Tuning): 将 Sigmoid 损失应用于 LiT 框架，即在预训练过程中锁定 (locked) 图像编码器，仅训练文本编码器。

• 可学习的偏置项 (learnable bias \(b\)): 在 Sigmoid 损失中引入的一个额外可学习参数。由于一个批次中负样本对的数量远超正样本对 ($$

  B

  ^2 -

  B

  \(vs\)

  B

  \()，存在严重的类别不平衡。引入偏置项\)b$$ 能够缓解此问题，确保训练在初始阶段更加稳定，避免因不平衡导致的剧烈梯度更新。

相关工作

当前，通过网络爬取的图文对进行对比预训练已成为获取通用计算机视觉骨干网络的主流方法，其代表性工作是 CLIP 和 ALIGN。这些方法通常采用基于 Softmax 的对比损失函数 (InfoNCE loss)。

然而，这种标准的 Softmax 损失存在一些关键问题：

1. 全局依赖性: 它需要在整个批次内计算所有图文对的相似度分数，并通过 Softmax 进行归一化，这导致损失计算与批次大小紧密耦合。

2. 高内存与计算开销: 在分布式训练中，计算全局归一化需要昂贵的 \(all-gather\) 操作来收集所有设备的嵌入向量，并且需要实例化一个大小为 $$

   B

   ×

   B

   $$ 的相似度矩阵，这极大地限制了批次大小的扩展。

3. 数值不稳定性: 朴素的 Softmax 实现存在数值不稳定问题，通常需要额外的计算步骤来稳定。

本文旨在解决上述问题，提出一种更简单、高效且与批次大小解耦的损失函数，以降低语言-图像预训练的资源门槛。

本文方法

本文首先回顾了标准的 Softmax 损失，然后详细介绍了其核心贡献——成对 Sigmoid 损失及其高效实现。

Softmax 损失回顾

对于一个包含 \(|B|\) 个图文对的批次，传统的对比学习目标是拉近匹配对 \((I_i, T_i)\) 的嵌入表示，同时推开不匹配对 \((I_i, T_j≠i)\) 的嵌入表示。使用 Softmax 损失函数，其目标函数如下：

\[-\frac{1}{2 \mid \mathcal{B} \mid }\sum_{i=1}^{ \mid \mathcal{B} \mid } \left( \overbrace{\log \frac{e^{t\mathbf{x}_i \cdot \mathbf{y}_i}}{\sum_{j=1}^{ \mid \mathcal{B} \mid } e^{t\mathbf{x}_i \cdot \mathbf{y}_j}}}^{\text{image\_softmax}} + \log \frac{e^{t\mathbf{x}_i \cdot \mathbf{y}_i}}{\sum_{j=1}^{ \mid \mathcal{B} \mid } e^{t\mathbf{x}_j \cdot \mathbf{y}_i}} \right).\]

其中 \(x\) 和 \(y\) 分别是归一化后的图像和文本嵌入，\(t\) 是一个可学习的温度参数。该损失函数需要对图像和文本分别进行两次独立的归一化。

创新点：Sigmoid 损失

与上述方法不同，本文提出的 Sigmoid 损失将问题转化为对所有可能的图文对进行二元分类。其定义如下：

\[-\frac{1}{ \mid \mathcal{B} \mid }\sum_{i=1}^{ \mid \mathcal{B} \mid }\sum_{j=1}^{ \mid \mathcal{B} \mid }\log\frac{1}{1+e^{z_{ij}\left(-t\mathbf{x}_{i}\cdot\mathbf{y}_{j}+b\right)}},\]

其中，\(z_ij\) 是标签，如果图文对 \((i, j)\) 是匹配的（即 \(i=j\)），则 \(z_ij = 1\)，否则 \(z_ij = -1\)。\(t\) 是可学习的温度参数，\(b\) 是为了应对正负样本严重不平衡而引入的可学习偏置项。这种设计将全局的对比学习问题分解为一系列独立的、局部的二元分类子问题。

\(Sigmoid loss\) 的伪代码实现如下：

算法 1 Sigmoid 损失伪代码实现

``\(python 1 # img_emb : 图像模型嵌入 [n, dim] 2 # txt_emb : 文本模型嵌入 [n, dim] 3 # t_prime, b : 可学习的温度和偏置 4 # n : mini-batch 大小 5 6 t = exp(t_prime) 7 zimg = l2_normalize(img_emb) 8 ztxt = l2_normalize(txt_emb) 9 logits = dot(zimg, ztxt.T) * t + b 10 labels = 2 * eye(n) - ones(n) # -1, 对角线为 1 11 l = -sum(log_sigmoid(labels * logits)) / n\)`$$

优点：高效的“分块”实现

Sigmoid 损失的独立性使其能够采用一种内存高效的“分块” (chunked) 实现方式，特别适用于分布式数据并行训练。

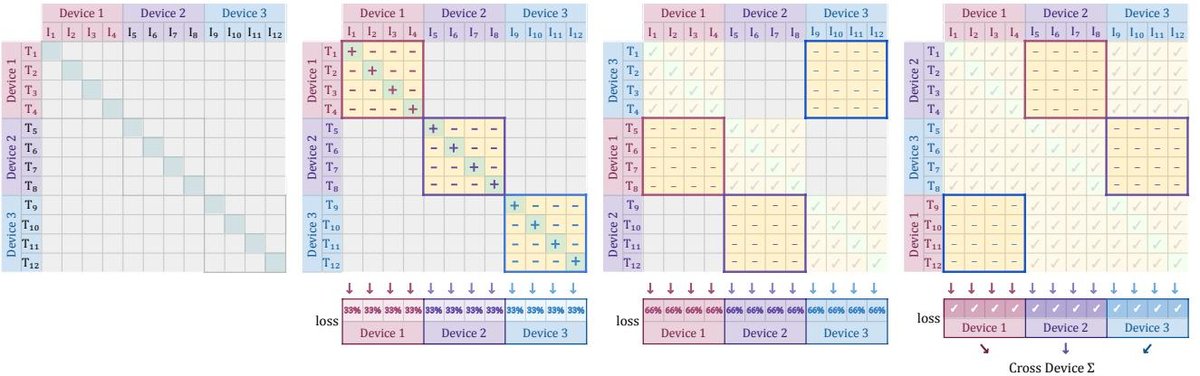图1：高效损失实现流程示意图。通过在设备间交换文本表征，避免了全局的 all-gather 操作和实例化大型相似度矩阵。

该实现的核心思想是避免一次性计算和存储整个 \(|B| × |B|\) 的相似度矩阵。具体步骤如下：

1. 在每个设备上，首先计算其本地批次内的相似度，包括正样本对和部分负样本对。
2. 然后，通过设备间的循环排列（collective permutes）操作，每个设备将其本地的文本嵌入发送给“邻居”设备。
3. 每个设备接收到新的文本嵌入“块”后，本地的图像嵌入与这个新的文本嵌入块计算损失，并累加。
4. 重复此过程 \(D-1\) 次（\(D\) 为设备数），直到所有图文对的组合都被计算过。

这种方式的优势在于：

• 内存高效: 在任何时刻，每个设备上只需要存储一个大小为 \(b × b\)（\(b\) 为单设备批次大小）的小块矩阵，而不是 $$

  B

  ×

  B

  $$ 的全局矩阵。

• 计算高效: \(D\) 次独立的 \(permute\) 操作通常比两次全局的 \(all-gather\) 操作更快。 正是这种高效的实现，使得本文能够将批次大小扩展到一百万。

实验结论

Sigmoid 损失与 Softmax 损失的对比

• 小批量优势显著: 在批次大小低于 16k 时，Sigmoid 损失的性能显著优于 Softmax 损失。
• 大批量性能相当: 随着批次大小增加，Softmax 的性能追赶上来，但 Sigmoid 损失仍然保持同等或略优的性能，同时在计算和内存上更具优势。

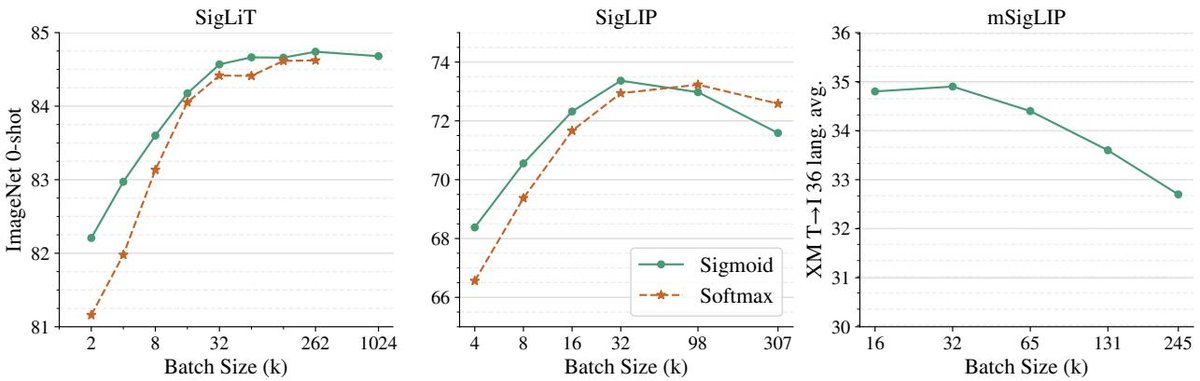图2：预训练批次大小的影响。左图 (SigLiT) 和中图 (SigLIP) 显示，Sigmoid 损失在小批量时优势明显，且两种损失的性能都在批次大小约为 32k 时达到饱和。

批次大小的影响

一个令人惊讶的核心发现是：对比学习的性能并非随着批次大小的增大而无限提升。

• 性能饱和点: 实验表明，无论使用 Sigmoid 还是 Softmax 损失，模型性能在大约 32k 的批次大小就已接近饱和。继续增加批次大小（即使到一百万）带来的性能提升非常有限，甚至可能导致性能下降。
• 多语言场景: 在包含 100 多种语言的多语言预训练 (mSigLIP) 中，32k 的批次大小同样是足够的，更大的批次反而损害了跨语言检索任务的性能。

Batch Size	16k	32k	64k	128k	240k
INet-0	71.6	73.2	73.2	73.2	73.1
XM avg	34.8	34.9	34.4	33.6	32.7

表格：mSigLIP 在不同批次大小下的性能。ImageNet 零样本准确率 (INet-0) 和 XM3600 平均检索性能 (XM avg) 均在 32k 批次大小达到峰值。

训练效率与可及性

• Sigmoid 损失的内存效率使其在有限的计算资源下也能进行有效的预训练。例如，使用 SigLiT 方法，在仅有 4 个 TPUv4 芯片的情况下，训练两天即可在一个强大的 ViT-g/14 视觉骨干上达到 84.5% 的 ImageNet 零样本准确率。
• 使用 SigLIP 从头训练一个 B/16 模型，在 32 个 TPUv4 上训练 5 天即可达到 73.4% 的准确率，相比 CLIP 等先前工作大幅降低了训练成本。

消融研究与发现

• 偏置项的重要性: 实验证明，在 Sigmoid 损失中引入并合理初始化偏置项 \(b\)（如 \(-10\)）对稳定训练和提升最终性能至关重要。
• 稳定性: 在大批量训练中，将 Adam 或 AdaFactor 优化器的 \(β2\) 参数从 \(0.999\) 降至 \(0.95\)，可以有效抑制梯度尖峰，稳定训练过程。
• 负样本比例: 通过实验（随机、难、易样本采样）发现，尽管负样本数量远多于正样本，但这种不平衡似乎不是一个主要问题。挖掘更多难负样本可能是有益的，但并非简单地增加负样本数量。

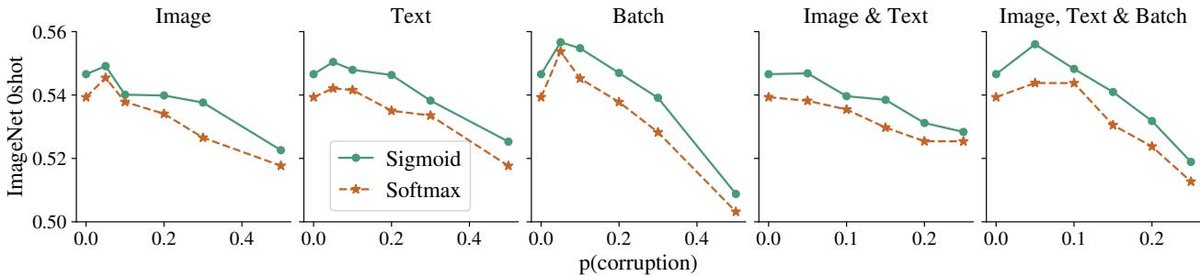图7：Sigmoid 训练对数据噪声的鲁棒性。结果显示，在图像、文本或批次对齐被不同概率 $$p` 破坏时，使用 Sigmoid 损失训练的模型始终比使用 Softmax 的模型表现出更强的鲁棒性。

最终结论

本文提出的 Sigmoid 损失在小批量场景下显著优于传统的 Softmax 损失，并且因其内存和计算效率，使得在有限资源下进行大规模语言-图像预训练成为可能。研究还揭示了对比学习中批次大小的收益会快速饱和，一个中等大小（如 32k）的批次已足够获得接近最优的性能。最终，经过充分训练的 SigLIP 模型在多个零样本分类和图文检索基准上取得了业界领先（SOTA）的性能。

ViT size	# Patches	ImageNet-1k	COCO R@1 (T→I)	COCO R@1 (I→T)
SigLIP (B)	576	78.6	49.7	67.5
SigLIP (L)	576	82.1	52.7	70.6
SigLIP (SO 400M)	729	83.2	52.0	70.2
OpenCLIP (G 2B)	256	80.1	51.4	67.3
EVA-CLIP (E 5B)	256	82.0	51.1	68.8

表格：与公开发布模型的性能对比。SigLIP 模型在不同尺寸下均优于或可比于参数量大得多的模型。