SimPO: Simple Preference Optimization with a Reference-Free Reward
-
ArXiv URL: http://arxiv.org/abs/2405.14734v3
-
作者: Danqi Chen; Mengzhou Xia; Yu Meng
-
发布机构: Princeton University; University of Virginia
TL;DR
本文提出了一种名为 SimPO 的简单偏好优化算法，它通过使用一个无需参考模型、与生成过程对齐的长度归一化奖励，在提升模型性能的同时，显著提高了训练的计算和内存效率。
关键定义
本文的核心创新在于对奖励函数和优化目标的重新设计，关键定义如下：
-
长度归一化的无参考奖励 (Length-normalized Reference-Free Reward)：这是 SimPO 的核心。它将隐式奖励函数定义为模型自身生成序列的平均对数概率，公式为 \(\)r_{\text{SimPO}}(x,y)=\frac{\beta}{ y }\log\pi_{\theta}(y\mid x)\(\)。这个定义有两个关键点： - 无参考 (Reference-Free)：与 DPO 不同，该奖励的计算仅依赖于当前策略模型 \($\pi\_{\theta}\)$，无需加载并维护一个额外的参考模型 \($\pi\_{\text{ref}}\)$，因此更简单、高效。
- 长度归一化 (Length-normalized)：通过除以序列长度 \($ \mid y \mid\)$，该奖励直接优化的是平均对数概率，这与模型在推理时（例如在束搜索中）评估生成质量的度量标准保持一致，有效避免了模型为了追求高奖励而盲目生成更长序列（即长度偏见）。
- 目标奖励边际 (Target Reward Margin, $\gamma$)：SimPO 在标准的 Bradley-Terry 偏好模型中引入了一个正的边际项 \($\gamma\)$。新的偏好概率公式为 \(\)p(y_{w}\succ y_{l}\mid x)=\sigma\left(r(x,y_{w})-r(x,y_{l})-\gamma\right)\(\)。这个边际项的作用是激励模型学习出一个更大的决策边界，使得偏好回复（winning response）\($y\_w\)$的奖励不仅要高于不偏好回复（losing response）\($y\_l\)$，而且要高出至少 \($\gamma\)$，从而增强模型的泛化能力。
相关工作
当前，利用人类反馈进行强化学习（Reinforcement Learning from Human Feedback, RLHF）是使大语言模型与人类意图对齐的关键技术。传统的RLHF流程（如PPO）包含训练奖励模型和策略优化两个阶段，过程复杂且优化不稳定。
为了简化这一流程，直接偏好优化（Direct Preference Optimization, DPO）被提出。DPO通过重参数化技巧，将奖励函数用策略模型和参考模型之间的对数概率比来表示，从而可以直接从偏好数据中优化策略模型，无需显式训练奖励模型。DPO因其简单和稳定而得到广泛应用。
然而，DPO存在一个关键问题：其隐式奖励函数 \($\beta\log\frac{\pi\_{\theta}(y\mid x)}{\pi\_{\text{ref}}(y\mid x)}\)$ 与模型在生成时实际优化的度量（近似为平均对数似然 \($\frac{1}{ \mid y \mid }\log\pi\_{\theta}(y\mid x)\)$）之间存在不一致性。这意味着，即使在训练中满足了DPO的奖励排序 \($r(x,y\_w) > r(x,y\_l)\)$，也不保证模型在生成时会认为 \($y\_w\)$ 的似然度高于 \($y\_l\)$。本文旨在解决这一训练与推理之间的不一致性，并进一步简化优化过程，提出一个更有效且高效的偏好学习算法。
本文方法
DPO的局限性与SimPO的设计动机
DPO的隐式奖励依赖于策略模型 \($\pi\_{\theta}\)$ 和参考模型 \($\pi\_{\text{ref}}\)$ 的概率比值，这带来了两个问题：
- 计算开销：训练时需要同时在内存中保留策略模型和参考模型，增加了计算和内存成本。
- 目标不匹配：DPO优化的奖励目标与模型生成时评估序列优劣的度量（平均对数概率）不一致。实验发现，经过DPO训练后，对于训练数据，奖励函数认为 \($y\_w\)$ 优于 \($y\_l\)$ 的情况中，有近一半的样本其平均对数概率反而是 \($p\_{\theta}(y\_w \mid x) < p\_{\theta}(y\_l \mid x)\)$。
图1：SimPO 和 DPO 的主要区别在于其奖励公式（阴影框中所示）。
为此，SimPO被设计出来，其核心思想是让训练目标直接与生成度量对齐。
创新点
无参考的长度归一化奖励
为了解决上述问题，本文提出了一个简单直观的奖励函数：
\[r_{\text{SimPO}}(x,y)=\frac{\beta}{ \mid y \mid }\log\pi_{\theta}(y\mid x)=\frac{\beta}{ \mid y \mid }\sum_{i=1}^{ \mid y \mid }\log\pi_{\theta}(y_{i}\mid x,y_{<i})\]这个奖励直接使用了模型对序列的平均对数概率。这种设计的优点是：
- 对齐训练与生成：奖励函数与模型生成时（如束搜索）的排序标准完全对齐。
- 消除参考模型：奖励的计算不再需要参考模型 \($\pi\_{\text{ref}}\)$，使得算法更简单，训练更高效。
- 缓解长度偏见：直接优化总对数概率会导致模型偏爱短序列。通过除以长度 \($ \mid y \mid\)$ 进行归一化，可以有效避免模型利用长度捷径，防止因惩罚长序列而导致的质量下降。
目标奖励边际 \($\gamma\)$
在标准的Bradley-Terry偏好模型的基础上，本文引入了一个目标奖励边际（target reward margin）\($\gamma > 0\)$，将偏好概率建模为：
\[p(y_{w}\succ y_{l}\mid x)=\sigma\left(r(x,y_{w})-r(x,y_{l})-\gamma\right)\]加入 \($\gamma\)$ 的目的是促使模型学到更强的区分能力，确保偏好回复的奖励值能够显著超过非偏好回复，而不仅仅是略微高出。这有助于提升模型的泛化性能。
SimPO 目标函数
结合上述两点，SimPO的最终损失函数被定义为：
\[\mathcal{L}_{\text{SimPO}}(\pi_{\theta})=-\mathbb{E}_{(x,y_{w},y_{l})\sim \mathcal{D}}\left[\log\sigma\left(\frac{\beta}{ \mid y_{w} \mid }\log\pi_{\theta}(y_{w} \mid x)-\frac{\beta}{ \mid y_{l} \mid }\log\pi_{\theta}(y_{l} \mid x)-\gamma\right)\right]\]其中 \($(x,y\_w,y\_l)\)$ 是来自偏好数据集 \($\mathcal{D}\)$ 的样本。该目标函数通过最大化偏好对数似然来优化策略模型 \($\pi\_{\theta}\)$。
防止灾难性遗忘
尽管SimPO没有像DPO一样显式地使用KL散度进行正则化来防止模型偏离初始SFT模型太远，但本文发现，通过结合以下实践因素，可以有效防止灾难性遗忘：
- 使用较小的学习率。
- 使用覆盖领域和任务广泛的偏好数据集。
- 大语言模型本身具有一定的鲁棒性，能够在学习新知识的同时不遗忘先验知识。
实验结论
性能对比
本文在多种模型（Mistral-7B, Llama-3-8B, Gemma-2-9B）和两种训练设置（Base 和 Instruct）下，将 SimPO 与 DPO 及其多种变体（如 IPO, ORPO, CPO 等）进行了广泛比较。
| 模型 | LC (%) | WR (%) | 长度 |
|---|---|---|---|
| Gemma-2-9B-it-SimPO | 72.4 | 65.9 | 1833 |
| GPT-4 Turbo (04/09) | 55.0 | 46.1 | 1802 |
| Gemma-2-9B-it | 51.1 | 38.1 | 1571 |
| Llama-3-8B-Instruct-SimPO | 44.7 | 40.5 | 1825 |
| Claude 3 Opus | 40.5 | 29.1 | 1388 |
| Llama-3-8B-Instruct-DPO | 40.3 | 37.9 | 1837 |
| Llama-3-70B-Instruct | 34.4 | 33.2 | 1919 |
| Llama-3-8B-Instruct | 26.0 | 25.3 | 1899 |
表1：在AlpacaEval 2排行榜上顶级模型的长度控制（LC）和原始胜率（WR）及生成长度。黑体为本文训练的模型。
主要发现：
- SimPO 显著且一致地优于现有方法：在 AlpacaEval 2、Arena-Hard 和 MT-Bench 三大主流基准测试上，SimPO 的性能全面超越 DPO 及其变体。例如，在 AlpacaEval 2 上，SimPO 相较于 DPO 带来了高达 6.4 个点的胜率提升；在更具挑战性的 Arena-Hard 上，提升高达 7.5 个点。
- 达到 SOTA 水平：基于 Gemma-2-9B-it 训练的 SimPO 模型，在 AlpacaEval 2 上取得了 72.4% 的长度控制胜率，并在 Chatbot Arena 排行榜上成为 100亿参数以下模型的第一名。
- 无明显长度利用：SimPO 在取得性能提升的同时，并没有显著增加生成回复的长度，这表明其长度归一化机制有效地防止了模型通过“说废话”来刷分。
| 方法 | Mistral-Base (7B) AlpacaEval 2 LC (%) |
Mistral-Instruct (7B) AlpacaEval 2 LC (%) |
Llama-3-Base (8B) AlpacaEval 2 LC (%) |
Llama-3-Instruct (8B) AlpacaEval 2 LC (%) |
|---|---|---|---|---|
| SFT | 8.4 | 17.1 | 6.2 | 26.0 |
| DPO [66] | 15.1 | 26.8 | 18.2 | 40.3 |
| ORPO [42] | 14.7 | 24.5 | 12.2 | 28.5 |
| SimPO | 21.5 | 32.1 | 22.0 | 44.7 |
表4（节选）：在AlpacaEval 2上，SimPO在所有设置中均显著优于SFT、DPO和ORPO等基线。
消融研究与分析
- 长度归一化（LN）至关重要：消融实验显示，如果移除 SimPO 奖励函数中的长度归一化项（w/o LN），模型性能会急剧下降。分析发现，没有长度归一化的模型会倾向于生成更长的回复以获得更高的奖励（总对数概率），导致了严重的长度利用和质量退化。
- 目标边际 \($\gamma\)$ 的作用：将 \($\gamma\)$ 设置为 0 会导致性能下降，证明了引入一个正的目标边际是有益的。实验表明，随着 \($\gamma\)$ 增大，奖励准确率（模型对偏好对的排序能力）会提升，但生成质量（胜率）会先升后降。这说明存在一个最优的 \($\gamma\)$ 值，过大的 \($\gamma\)$ 可能会导致模型过分关注奖励差异而损害生成概率的校准。
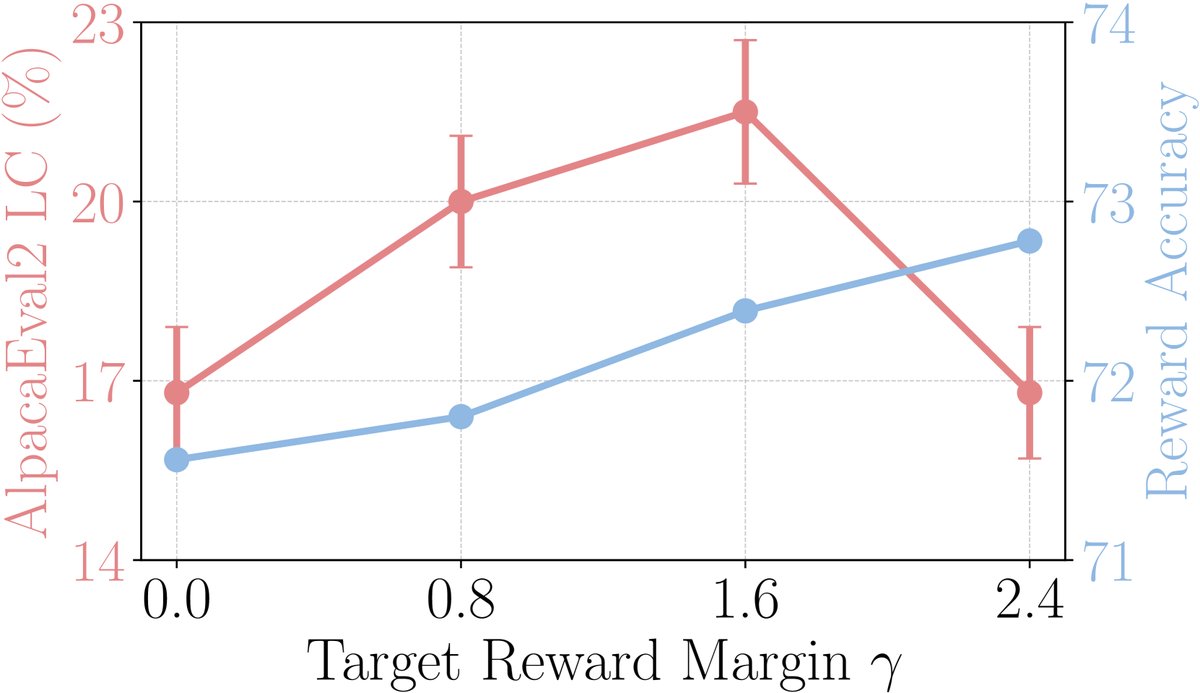图3(a)：不同 \($\gamma\)$ 值对奖励准确率和 AlpacaEval2 胜率的影响。
SimPO vs. DPO 深入对比
- 奖励准确率：SimPO 在验证集上实现了比 DPO 更高的奖励准确率，表明其学习到的奖励函数更好地泛化到了未见过的数据上，这直接转化为更高质量的生成策略。
- 训练效率：由于无需加载参考模型，SimPO 在训练时比 DPO 更快，且内存占用更低。例如，在A100 GPU上，SimPO的训练时间减少了约12%，内存消耗减少了约16%。
- KL 散度：尽管 SimPO 没有显式的 KL 正则项，但实验表明，其策略模型与初始 SFT 模型之间的 KL 散度与 DPO 处在相似的低水平，说明在实践中（小学习率等因素），SimPO 同样能有效防止灾难性遗忘。
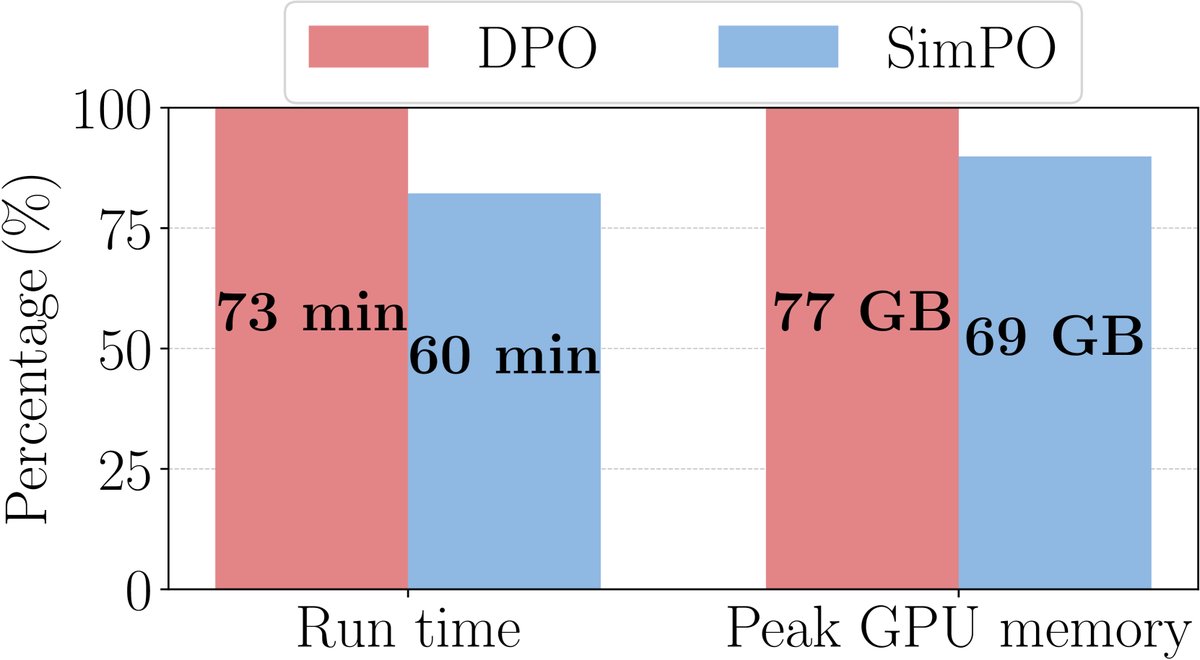图5(c)：DPO 与 SimPO 的运行时间和内存使用对比。
最终结论
SimPO 作为一种偏好优化算法，通过引入一个与生成过程对齐的、无参考模型的长度归一化奖励，并结合目标奖励边际，成功地解决了 DPO 中训练与推理目标不匹配的问题。它不仅在概念上更简单、在计算上更高效，而且在多个主流基准上一致且显著地优于 DPO 及其变体，为大语言模型对齐提供了一个强大而简洁的新方案。