SparseGPT: Massive Language Models Can Be Accurately Pruned in One-Shot

TL;DR

本文提出了一种名为 SparseGPT 的新颖剪枝方法，能够对超大规模语言模型（如 OPT-175B）进行一次性（One-Shot）剪枝，在不进行任何重新训练的情况下，达到50%-60%的稀疏度，同时保持极低的准确率损失。

关键定义

本文主要沿用并扩展了领域内已有的关键定义，其核心贡献在于解决这些定义所引出问题的全新算法。

  1. 逐层剪枝 (Layer-Wise Pruning)：将整个模型的压缩问题分解为一系列独立的、针对每一层的子问题。对于每一层 \(l\)，目标是找到一个稀疏掩码 \(M_l\) 和更新后的权重 \(\widehat{\mathbf{W}}_{\ell}\)，以最小化剪枝前后层输出之间的 \(L2\) 误差。其目标函数为：

    \[\operatorname{argmin}_{\max \mathbf{M}_{\ell}, \widehat{\mathbf{W}}_{\ell}} \mid \mid \mathbf{W}_{\ell} \mathbf{X}_{\ell} - (\mathbf{M}_{\ell} \odot \widehat{\mathbf{W}}_{\ell}) \mathbf{X}_{\ell} \mid \mid _2^2\]
  2. 权重重构 (Weight Reconstruction)：在确定了要剪枝的权重（即固定了掩码 \(M\)）之后，调整剩余未剪枝的权重，以补偿因剪枝造成的精度损失。
  3. Hessian 矩阵：在逐层剪枝问题中，Hessian矩阵 \(H\) 定义为输入激活的二阶矩，即 \(H = XX^T\)。该矩阵的逆 \(H^{-1}\) 对于计算剪枝一个权重后其他权重的最优更新至关重要。

相关工作

当前，大型语言模型（LLM）因其巨大的参数量和计算成本而难以部署。模型压缩是解决此问题的关键路径，主要包括量化和剪枝。

本文方法

方法动机：精确重构的扩展性瓶颈

对于一个给定的剪枝掩码 \(M\)，最优的权重重构需要对每一行 \(i\) 分别求解一个稀疏回归问题。这涉及到计算并求逆一个与该行特定掩码相关的 Hessian 子矩阵 \(H_{M_i}\)。由于每一行的剪枝掩码 \(M_i\) 都不同，导致需要对 \(d_{row}\) 行中的每一行都进行一次独立的 \(O(d_{col}^3)\) 复杂度的矩阵求逆，总复杂度高达 \(O(d_{row} \cdot d_{col}^3)\)。对于 Transformer 模型中的 \(d_{hidden} \times d_{hidden}\) 矩阵，其复杂度为 \(O(d_{hidden}^4)\)，这在计算上是不可行的。

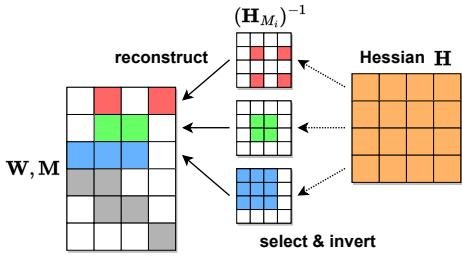Refer to caption 图3：行-Hessian 挑战图示：各行独立稀疏化，不同行的掩码不同导致无法共享Hessian逆矩阵的计算。

核心机制：Hessian 同步与近似重构

SparseGPT 的核心创新在于设计了一种高效的近似重构算法，它巧妙地规避了为每行计算独立 Hessian 逆矩阵的瓶颈。

  1. 迭代视角：本文首先从 OBS (Optimal Brain Surgeon) 框架的迭代视角出发。剪掉一个权重 \(w_m\) 后，对剩余权重的最优更新 \(\delta\) 可以通过 \(H^{-1}\) 精确计算。通过迭代地、一次一个地剪掉所有待移除的权重，最终可以得到与直接求解稀疏回归问题相同的最优解。
  2. 部分更新：OBS 更新通常会调整所有未剪枝的权重。本文发现，可以只选择一个子集 \(U\) 的权重进行更新，这虽然可能降低补偿效果，但如果 \(U\) 较小，则计算 \(H_U\) 的逆会快得多。
  3. Hessian 同步：这是算法的关键。SparseGPT 按列顺序处理权重矩阵 \(W\)。对于每一列 \(j\)，它使用一个预先计算好的、共享的逆 Hessian 矩阵 \((H_{U_j})^{-1}\) 来执行剪枝操作。这里的 \(U_j\) 是一个递减的索引集 \(U_{j+1} = U_j - \{j\}\)。通过这种方式，所有行在处理同一列 \(j\) 时，都使用相同的逆 Hessian 矩阵。
  4. 高效实现：整个逆 Hessian 序列 \((H_{U_j})^{-1}\) 可以通过高斯消元法从初始的 \(H^{-1}\) 在 \(O(d_{col}^3)\) 时间内递归计算得出。这使得总的重构时间复杂度从 \(O(d_{row} \cdot d_{col}^3)\) 大幅降低到 \(O(d_{col}^3 + d_{row} \cdot d_{col}^2)\)，对于 Transformer 模型即为 \(O(d_{hidden}^3)\)，实现了关键的 \(d_{hidden}\) 倍加速。

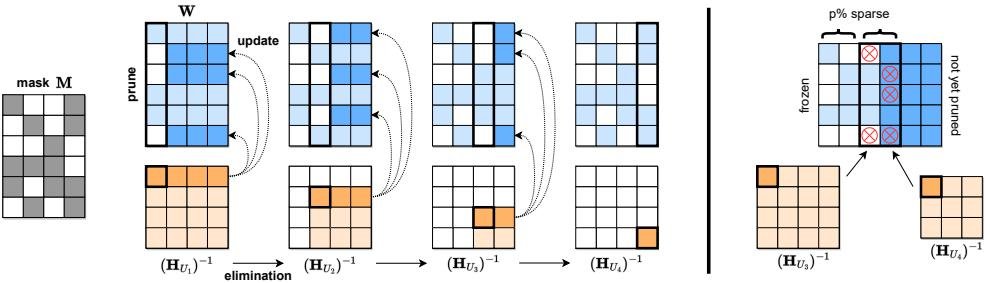Refer to caption 图4：SparseGPT 重构算法可视化。算法按列处理权重，并使用一系列共享的Hessian逆矩阵更新该列右侧的权重，以补偿剪枝误差。

自适应掩码选择

为了进一步提升精度，SparseGPT 并非使用固定的剪枝掩码，而是采用自适应掩码选择策略。它以 \(B_s = 128\) 列为一个块 (block)，在处理每个块之前，根据 OBS 误差准则（\(\varepsilon_m = w_m^2 / [H^{-1}]_{mm}\)）为这个块内的所有权重动态选择剪枝掩码。这使得剪枝决策能够考虑到之前权重更新带来的影响，并且允许稀疏度在不同列之间非均匀分布，从而保护那些对模型性能至关重要的“离群特征 (outlier features)”。

扩展能力

完整算法伪代码

算法1展示了集成所有优化技术的非结构化稀疏版 SparseGPT。

算法 1: SparseGPT 算法
输入: 权重矩阵 \(W\), 逆 Hessian \(H^{-1}\), 批更新块大小 \(B\), 自适应掩码块大小 \(B_s\), 稀疏度 \(p\)
\(M\) ← \(1^{d_{row} \times d_{col}}\) // 初始化二进制剪枝掩码
\(E\) ← \(0^{d_{row} \times B}\) // 块误差
\(H^{-1}\) ← \(Cholesky(H^{-1})^T\) // Cholesky分解以获取Hessian逆信息
for \(i = 0, B, 2B, ...\) do
    for \(j = i, ..., i + B - 1\) do
        if \(j mod B_s == 0\) then
            \(M[:, j:(j+B_s)]\) ← 根据 \(w_c^2 / [H^{-1}]_{cc}\) 在 \(W[:, j:(j+B_s)]\) 中选择 \((1-p)%\) 最大值的掩码
        end if
        \(err\) ← \((W[:, j] - E[:, j-i]) / [H^{-1}]_{jj}\) // 计算剪枝误差
        \(E[:, j-i]\) ← \((1 - M[:, j]) \cdot err\) // 累积被剪掉权重的误差
        \(W[:, j:(i+B)]\) ← \(W[:, j:(i+B)] - E[:, j-i] \cdot H^{-1}_{j, j:(i+B)}\) // 更新权重
    end for
    \(W[:, (i+B):]\) ← \(W[:, (i+B):] - E \cdot H^{-1}_{i:(i+B), (i+B):}\) // 批处理更新
end for
\(W\) ← \(W \odot M\) // 将剪枝后的权重设为0

实验结论

本文在一系列超大规模模型（OPT 和 BLOOM 系列）上进行了广泛实验，所有实验均在单张 A100 GPU 上完成，结果令人瞩目。

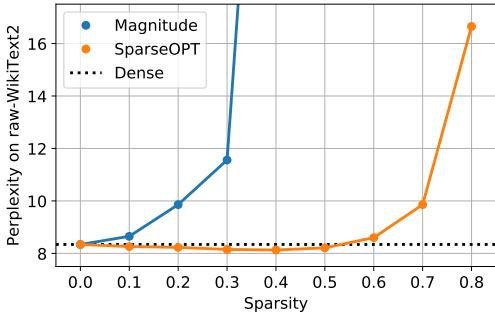Refer to caption 图1：OPT-175B 上 SparseGPT 与幅度剪枝的稀疏度-困惑度对比。

Refer to caption 图2：使用SparseGPT将OPT模型家族压缩到不同稀疏模式时的困惑度对比。

OPT - 50% 稀疏度 125M 350M 1.3B 2.7B 6.7B 13B 30B 66B 175B
Dense 27.66 22.00 14.62 12.47 10.86 10.13 9.56 9.34 8.35
Magnitude 193. 97.80 1.7e4 265. 969. 1.2e4 168. 4.2e3 4.3e4
SparseGPT 36.85 31.58 17.46 13.48 11.55 11.17 9.79 9.32 8.21
SparseGPT 4:8 58.66 48.46 32.52 14.98 12.56 11.77 10.30 9.65 8.45
SparseGPT 2:4 - - - 17.18 14.20 12.96 10.90 10.09 8.74
方法 稀疏度 Lambada PIQA ARC-e ARC-c Story. 平均
Dense 0% 75.59 81.07 71.04 43.94 79.82 70.29
Magnitude 50% 00.02 54.73 28.03 25.60 47.10 31.10
SparseGPT 50% 78.47 80.63 70.45 43.94 79.12 70.52
SparseGPT 4:8 80.30 79.54 68.85 41.30 78.10 69.62
SparseGPT 2:4 80.92 79.54 68.77 39.25 77.08 69.11