Stream: Scaling up Mechanistic Interpretability to Long Context in LLMs via Sparse Attention
-
ArXiv URL: http://arxiv.org/abs/2510.19875v1
-
作者: Hugues Bouchard; Konstantina Palla; Gustavo Penha
-
发布机构: Spotify; University of Oxford
TL;DR
本文提出了一种名为 Stream 的可解释性框架,通过其具体实现算法 Stream-Attn,利用动态稀疏注意力机制,以近线性的时间($O(T\log T)$)和线性空间($O(T)$)复杂度,高效分析大型语言模型在百万级Token长上下文中的注意力模式,从而在消费级GPU上实现了以往难以企及的机理可解释性分析。
关键定义
本文沿用了领域内的现有定义,并在此基础上提出了新的框架和算法:
- Stream (Scalable Transformer Reasoning and Elicitation via Attention Masks): 本文提出的一个机理可解释性算法框架,旨在利用稀疏注意力高效分析长上下文场景下的注意力模式。其核心思想是,通过剪枝掉冗余的注意力连接,既能解决分析的计算瓶颈,又能凸显出关键的信息流。
- Stream-Attn: 本文提出的一个具体算法,是 Stream 框架的实例化。它基于分层剪枝注意力(HiP Attention)算法,通过一种类似二分搜索的精炼过程,为每个查询(Query)动态地保留最重要的前 $k$ 个键(Key)块,从而生成一个稀疏的注意力掩码。该算法可在近线性时间内完成,且其粒度(如句子级、段落级)可通过块大小参数进行调整。
- 思想锚点 (Thought Anchors): 指在推理链条中对后续思考过程产生不成比例的巨大影响的关键步骤或句子。本文验证了 Stream-Attn 能够有效地在长上下文中识别出这些锚点。
- 接收头 (Receiver Heads): 指那些倾向于将注意力集中在上下文中少数几个关键部分(即思想锚点)而不是广泛分散的注意力头。本文通过测量注意力分布的峰度(kurtosis)来识别这类注意力头。
相关工作
当前,机理可解释性领域的研究旨在逆向工程神经网络(如大型语言模型),以理解其内部工作机制。然而,传统分析技术(如直接分析注意力矩阵、激活补丁等)在应用于长上下文场景时面临严峻的扩展性挑战。
最关键的瓶颈在于,注意力机制的计算时间和内存使用量都与上下文长度 $T$ 呈二次方($O(T^2)$)关系。当上下文长度达到十万甚至百万级别时,仅仅为了缓存所有注意力头的注意力模式就需要数TB的内存,这在消费级硬件上是完全不可行的。因此,许多前沿的可解释性研究明确将超过数百Token的长上下文分析推迟到未来的工作中。
本文旨在直接解决这一核心痛点:开发一种可无缝扩展至十万级Token上下文,且能在消费级GPU上运行的可解释性技术,从而推动长上下文机理可解释性研究的普及化。
本文方法
Stream: 一种新颖的技术框架
本文引入了 Stream,一个利用稀疏注意力(Sparse Attention)来高效分析长上下文场景下注意力模式的机理可解释性技术框架。其核心假设是,注意力计算中的稀疏化方法不仅可以降低推理时的计算复杂度,同样也可以作为一种有效的“过滤器”,帮助可解释性研究识别出模型中与输出最相关的关键部分。传统的注意力分析与模型推理面临着相同的计算瓶颈,而 Stream 框架通过只计算和分析注意力模式中最相关的部分,从根本上解决了这个问题。与需要多次前向或后向传播的复杂技术不同,Stream 在已知稀疏度常数 $k$ 的情况下,仅需一次前向传播即可完成所有组件的分析。
Stream-Attn: 一种高效的算法实现
本文提出了 Stream-Attn 算法,作为 Stream 框架的具体实现。该算法深受分层剪枝注意力(Hierarchically Pruned (HiP) Attention)的启发,并沿用了其核心的分层搜索过程。
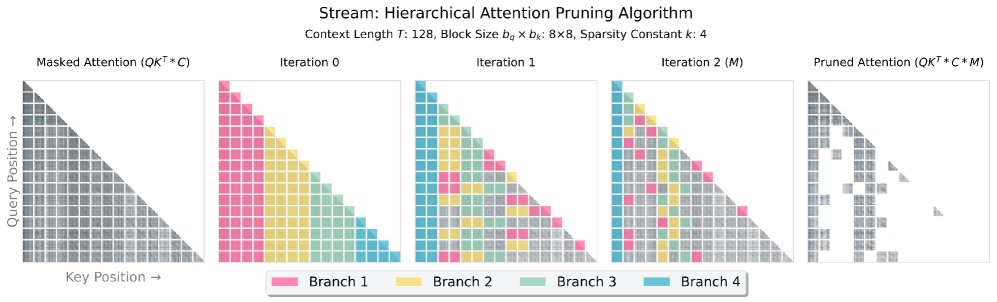
算法的核心机制如下:
- 分块 (Blocking): 首先,将完整的注意力矩阵按查询(Query)和键(Key)划分为大小为 $b_q$ 和 $b_k$ 的块。
- 分层搜索与剪枝 (Hierarchical Search & Pruning): 接着,算法采用一种类似二分搜索的策略来逐步缩小搜索范围,以找到每个查询块最相关的前 $k$ 个键块。初始时,它将整个键空间划分为 $k$ 个分支,然后迭代地评估并丢弃得分较低的分支,同时对保留的“有希望”的分支进行递归细分。
- 生成稀疏掩码 (Mask Generation): 这个过程持续进行,直到最终收敛到每个查询块对应的 $k$ 个得分最高的键块。最终,生成一个稀疏的二进制注意力掩码 $M$,仅保留这些最强的注意力连接。
该算法的行为由三个关键超参数控制:查询块大小 $b_q$、键块大小 $b_k$ 和稀疏度常数 $k$。通过调整块大小,可以实现不同语义粒度(如 $b_q=b_k=32$ 近似于句子级别)的分析。稀疏度常数 $k$ 则直接控制了剪枝的强度。
在实践中,本文的方法流程为:
- 使用指定的参数 $(b_q, b_k, k)$ 通过 Stream-Attn 计算出每层每个头的稀疏注意力掩码。
- 将掩码应用于完整的注意力模式,以识别最相关的注意力连接。
- 通过对稀疏度常数 $k$ 进行二分搜索,找到一个最小的 $k$ 值,该值能在剪枝后仍保留模型的原始行为(本文标准为:模型能连续生成两个与原始输出相同的Token)。
实验结论
本文通过两个案例研究,在不同的模型和任务上验证了 Stream-Attn 的有效性和可扩展性。
案例一:识别思维链中的“思想锚点”
本实验在 DeepSeek R1-Distill Qwen-1.5B模型上进行,旨在复现并扩展在长上下文(最高10,000个Token)中识别“思想锚点”的研究。
- 核心发现:
- 高效剪枝: Stream-Attn 能够在剪枝97-99%的注意力连接的同时,保持模型输出的正确性。这使得注意力模式的存储效率比密集模式高出28,000至68,000倍,且内存复杂度随上下文长度线性增长。
- 锚点识别: 尽管进行了大规模剪枝,稀疏注意力模式依然清晰地揭示了“思想锚点”。如下图所示,Stream-Attn 的结果(第三、四列)与完整的注意力模式(第一列)和块平均模式(第二列)在结构上高度一致,但计算成本极低。
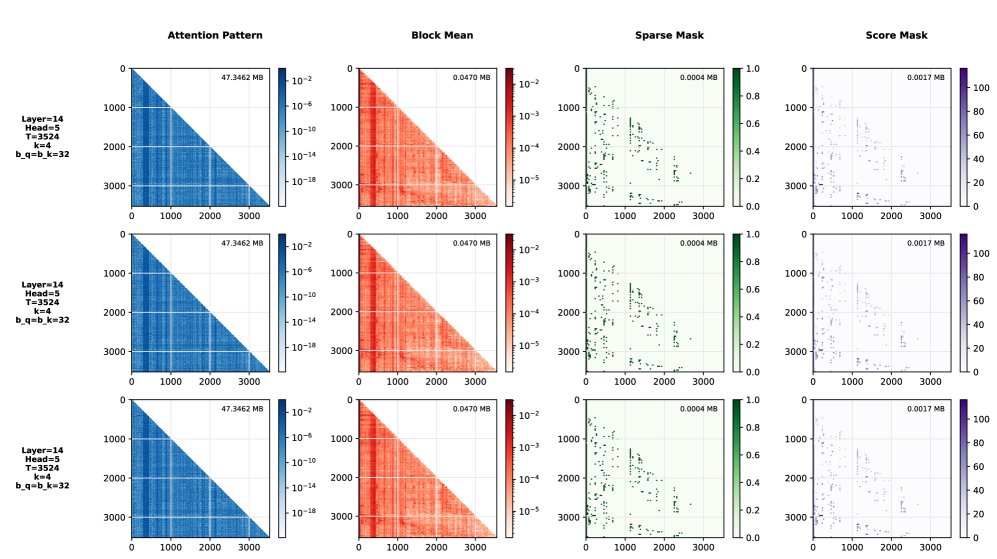
- 重要性分析: 分析发现,“问题设定 (problem setup)”和“最终答案生成 (final answer emission)”这两类句子块始终获得最强的下游注意力。在更长的推理轨迹中,“计划生成 (plan generation)”和“自我检查 (self-checking)”等步骤也显示出重要性。
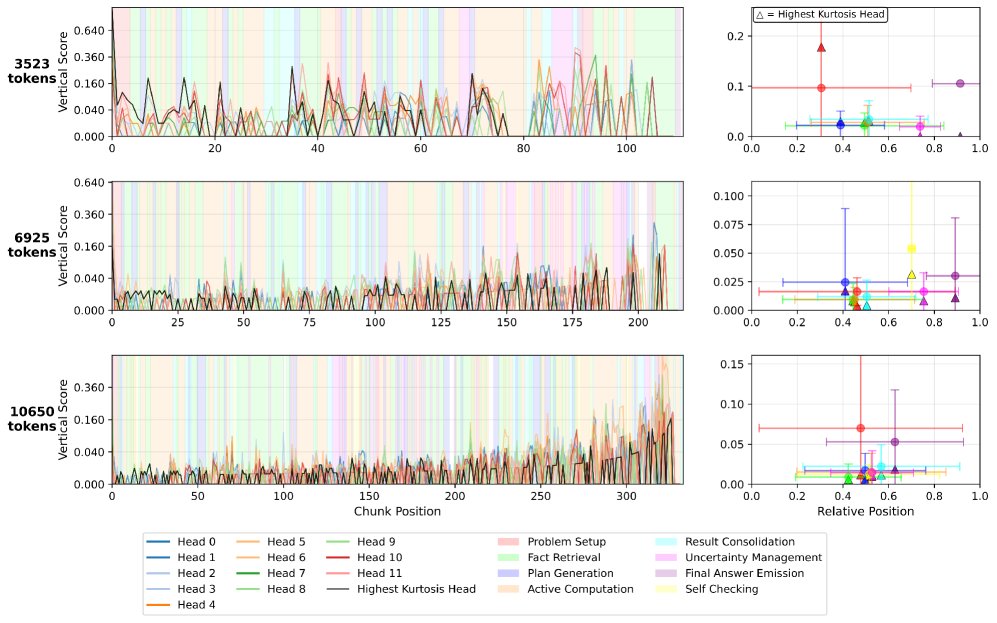
- 结论: 该实验证明 Stream-Attn 是一种高度可扩展的方法,能够以极低的资源成本在长上下文推理中有效识别关键的思考步骤。
案例二:大海捞针任务中的信息追踪
本实验在 Gemma 3 1B 模型上使用 RULER 基准进行,旨在验证 Stream-Attn 在长上下文信息检索任务中的表现。
- 核心发现:
- 保留关键路径: 在高达2万Token的上下文中,Stream-Attn 能够在丢弃90-96%注意力连接的情况下,完整保留从“针”(需要检索的信息)到最终输出的关键信息路径。如下图所示,稀疏掩码清晰地勾勒出了这条路径。
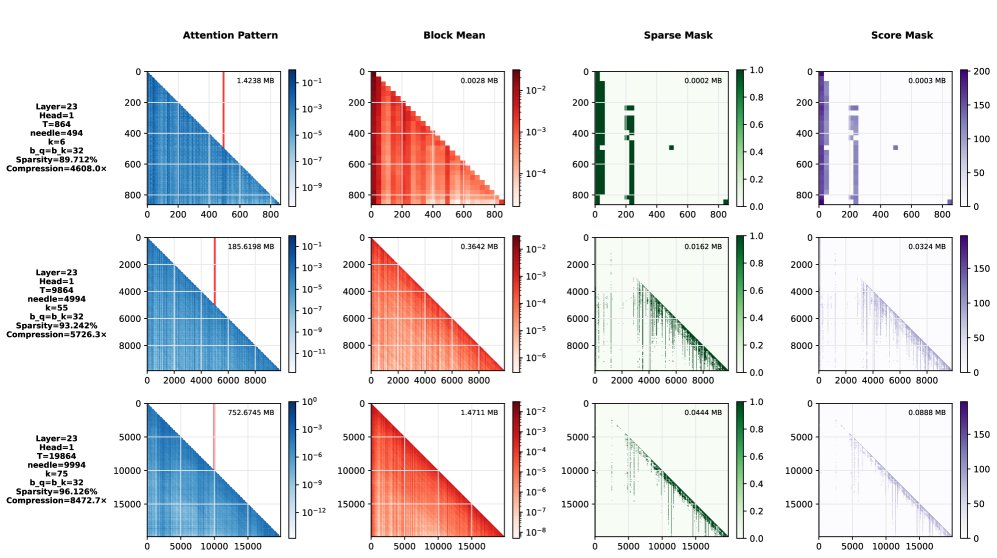
- 稀疏度与“针”位置的影响: 实验发现,当稀疏度较高时(如 $s \geq 0.1$),模型在检索位于上下文末尾的“针”时会失败。作者认为这是由于因果掩码的结构特性导致上下文末尾的剪枝更为激进,并提出未来研究中可采用可变稀疏度 $k$ 来解决此问题。

- 信息流可视化: 通过比较成功检索和失败检索时的稀疏注意力掩码差异,本文成功绘制出了信息从“针”所在位置流向输出的跨层路径图。这证明 Stream-Attn 可以作为一种经验工具,用于探索和验证关于信息如何在网络中传播的理论。
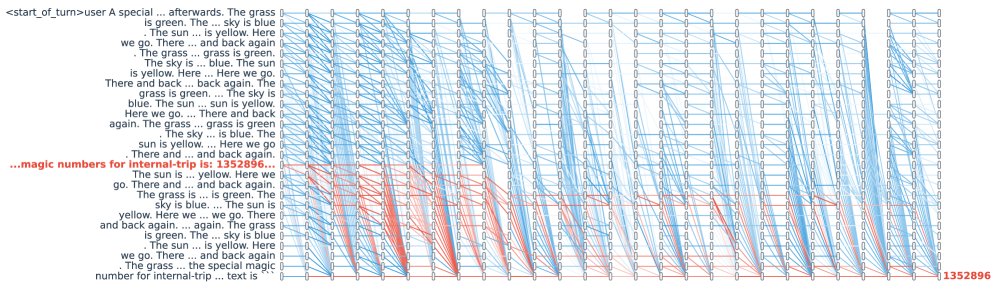
- 结论: 该实验表明,Stream-Attn 能够有效地追踪长上下文中的信息流,不仅验证了其在保留关键信号方面的能力,也使其成为研究信息传递机制(如信息过压缩)的可行工具。