The Universal Landscape of Human Reasoning

• ArXiv URL: http://arxiv.org/abs/2510.21623v1

• 作者: Yimeng Zhang; Jiannan Guan; Xie Chen; Jiaqi Wang; Mengkang Hu; Jinhao Liu; Zheng Yan; Wanxiang Che; Qiguang Chen; Yihao Liang; 等13人

• 发布机构: ByteDance; Central South University; Harbin Institute of Technology; Princeton University; Shanghai Jiao Tong University; The Chinese University of Hong Kong; The University of Hong Kong; University of Illinois Urbana-Champaign

---

TL;DR

本文提出了一种名为“信息流追踪”（Information Flow Tracking, IFT）的框架，该框架利用大语言模型（LLM）作为概率编码器，通过量化推理每一步的信息熵和信息增益，首次在统一的度量空间中对人类通用推理的动态过程进行建模。

关键定义

本文的核心是围绕一个新颖的理论框架展开的，其中包含以下关键定义：

1. 信息流追踪 (Information Flow Tracking, IFT)：一个用于定量描述人类推理动态过程的理论框架。它将推理视为一个连续的认知流，并通过追踪信息相空间中的轨迹来揭示推理的内在结构和模式。
2. 信息相空间 (Information Phase Space)：一个由两个正交维度构成的二维空间，用于描绘推理状态。这两个维度是“不确定性”和“认知努力”。推理过程表现为该空间中的一条轨迹。
3. 不确定性 (Uncertainty)：用于量化推理步骤中的模糊性或信息量。它通过计算一个推理步骤中所有Token的平均香农熵 (Shannon entropy) 来定义：\($u\_{t}=-\frac{1}{n\_{t}}\sum\_{i=1}^{n\_{t}}p\_{t,i}\log p\_{t,i}\)$，其中 \($p\_{t,i}\)$ 是LLM生成第 \($t\)$ 步中第 \($i\)$ 个Token的概率。
4. 认知努力 (Cognitive Effort)：用于量化连续推理步骤之间所需的信息重组量。它被定义为不确定性的时间导数，即相邻步骤间不确定性的变化量：\($e\_{t}=u\_{t}-u\_{t-1}\)$。它反映了从一个认知状态过渡到下一个状态所需的心智投入。

相关工作

当前对人类推理的研究方法，从经典的逻辑学、概率模型（如贝叶斯推理）到心理模型理论，虽然各有建树，但大多存在共同的局限性。这些方法主要关注推理的最终结果或提供静态的认知快照，例如使用t-SNE等技术对推理步骤进行嵌入可视化，但这会丢失过程中的时序信息，导致轨迹混乱且难以解释。即使是更先进的“思维景观”方法，在处理通用推理任务时也表现出不一致性。

现有研究普遍缺乏一个统一的、定量的框架来连续追踪通用的推理轨迹。这使得我们难以获得过程层面的机制性洞察，也无法揭示推理过程中的动态特征，如错误的产生模式、推理类型差异以及个体差异等。本文旨在解决这一关键问题，即建立一个能够定量、动态、统一地捕捉人类推理过程的通用模型。

本文方法

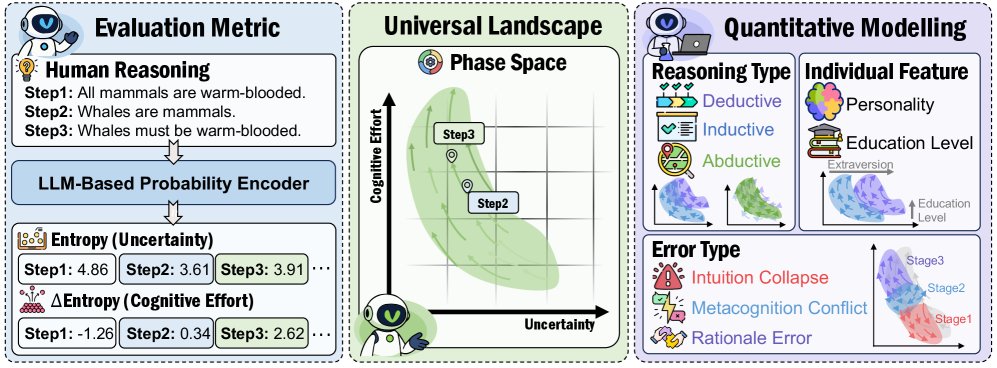
本文的核心方法是 信息流追踪 (IFT) 框架，它将认知科学的概念与物理学中的哈密顿动力学 (Hamiltonian Dynamics) 思想相结合，为人类推理过程提供了一个全新的定量分析视角。

理论基础：哈密顿动力学隐喻

本文借鉴哈密顿动力学来描述一个守恒系统。在物理学中，一个系统的状态由共轭变量（如位置 \($q\)$ 和动量 \($p\)$）定义，其演化在保持总能量 \($H(q,p)\)$ 守恒的相空间中进行。该理论启发本文将推理过程也看作一个类似的信息守恒系统。

IFT 框架

IFT框架将推理过程映射到一个二维的“信息相空间”中，该空间由不确定性 \($u\_t\)$ 和 认知努力 \($e\_t\)$ 这对共轭变量构成。

1. 状态定义：在任一推理步骤 \($t\)$，认知状态由一个点 \($(u_t, e_t)\)$$ 表示。
2. 量化计算：

   • 不确定性 \($u\_t\)$：利用LLM作为概率编码器，计算在生成第 \($t\)$ 步推理文本时，所有Token概率的平均香农熵。这反映了在该步骤生成内容时的内在模糊度。

     \[u_{t}=-\frac{1}{n_{t}}\sum_{i=1}^{n_{t}}p_{t,i}\log p_{t,i}\]

   • 认知努力 \($e\_t\)$：定义为相邻步骤间不确定性的变化量，即信息增益。它衡量了从一步到下一步认知状态的调整幅度。

     \[e_{t}=u_{t}-u_{t-1}=-\frac{1}{n_{t}}\sum_{i=1}^{n_{t}}p_{t,i}\log p_{t,i}+\frac{1}{n_{t-1}}\sum_{j=1}^{n_{t-1}}p_{t-1,j}\log p_{t-1,j}\]
3. 动态轨迹：整个推理过程形成一条从高不确定性、低认知努力的初始状态（直觉探索）向低不确定性、高认知努力的最终状态（审慎分析）演化的轨迹。

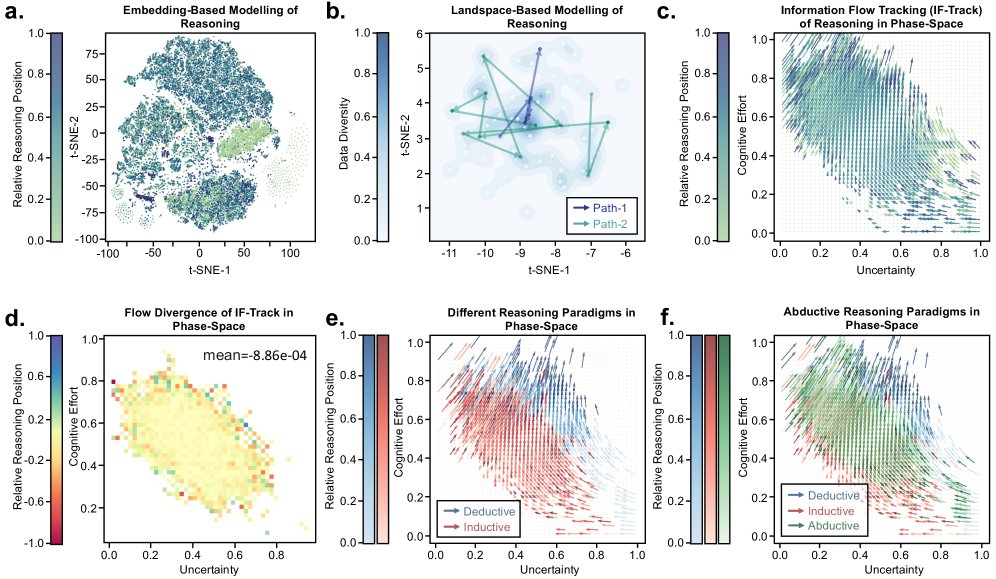
创新点

本文方法与以往最本质的区别在于，它首次将推理从静态分析转变为动态过程的定量追踪。其核心创新点在于：

1. 统一的度量空间：创建了一个通用的“信息相空间”，能够跨越不同任务、不同个体来统一描述和比较推理过程，解决了以往模型碎片化的问题。
2. 物理学类比的理论深度：将推理过程建模为近似哈密顿系统中的 几乎不可压缩信息流 (approximately incompressible information flow)。根据刘维尔定理 (Liouville’s theorem)，这种流的散度为零（ \($\nabla\!\cdot\!\vec{V} \approx 0\)$），意味着信息在相空间中的“体积”是守恒的。这为推理的连续性和结构性提供了深刻的理论支持。

优点

• 过程可解释性：IFT使推理的每一步都变得可量化和可视化，揭示了从直觉到分析的动态转变过程，而不仅仅是关注最终答案的对错。
• 通用性与可复现性：该框架适用于不同类型的推理任务（演绎、归纳、溯因），并能生成可复现的、具有一致流向的认知轨迹图谱。
• 精细化分析能力：能够精确识别推理过程中的错误模式、区分不同的推理类型，并量化个体差异（如性格、教育背景）对推理策略的影响。

实验结论

通用推理蓝图建模

• IFT的有效性：实验证明，与t-SNE等静态嵌入方法产生的混乱无序的可视化结果相比，IFT能将推理过程成功量化为信息相空间中结构清晰、方向一致的流场。如上图所示，IFT（右）生成的轨迹具有明确的从右下到左上的流向，而非推理任务则表现为无序动态。
• 哈密顿动力学假设的验证：通过计算推理轨迹上局部流场的散度，发现其值接近于零（图中大片黄色区域），证实了人类推理过程是一个近似的不可压缩信息流，符合刘维尔方程，为模型的理论基础提供了经验支持。

经典推理属性建模

区分经典推理类型

IFT通过轨迹模式成功地区分了三种经典的推理类型。

• 演绎与归纳推理：两者全局模式相似（不确定性下降，认知努力上升），但局部动态不同。演绎推理（Deductive reasoning）初始认知努力更高，不确定性下降更快，呈“自上而下”特征；归纳推理（Inductive reasoning）则相反，体现了“自下而上”的探索性。
• 溯因推理：其轨迹介于演绎和归纳之间，呈现出一种探索性假设生成和验证性推理相结合的混合动态模式。

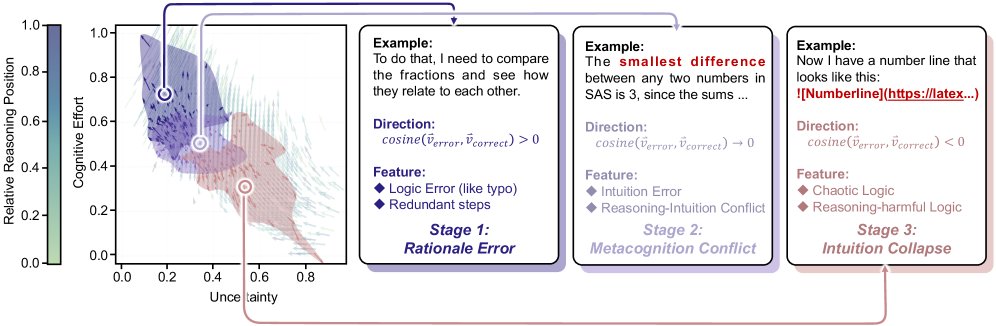
识别推理错误

IFT能够根据轨迹偏离正常流动的模式来有效识别和分类推理错误，且与Pennycook的三阶段错误理论吻合。

错误阶段	位置特征 (不确定性-努力)	轨迹特征 (与正确方向夹角)	认知解释
直觉失败 (Intuition Failure)	高不确定性, 低努力	方向相反 (\($\cos < 0\)$)	基于错误的直觉，推理在早期就已崩溃。
监控失败 (Monitoring Failure)	中等不确定性, 中等努力	方向垂直 (\($\cos \approx 0\)$)	推理看似连贯但基于错误假设，未能发现矛盾。
审慎失败 (Deliberation Failure)	低不确定性, 高努力	方向一致 ($$$\cos > 0$`)	推理结构正确，但存在冗余、计算失误等低效处理。

个体特征建模

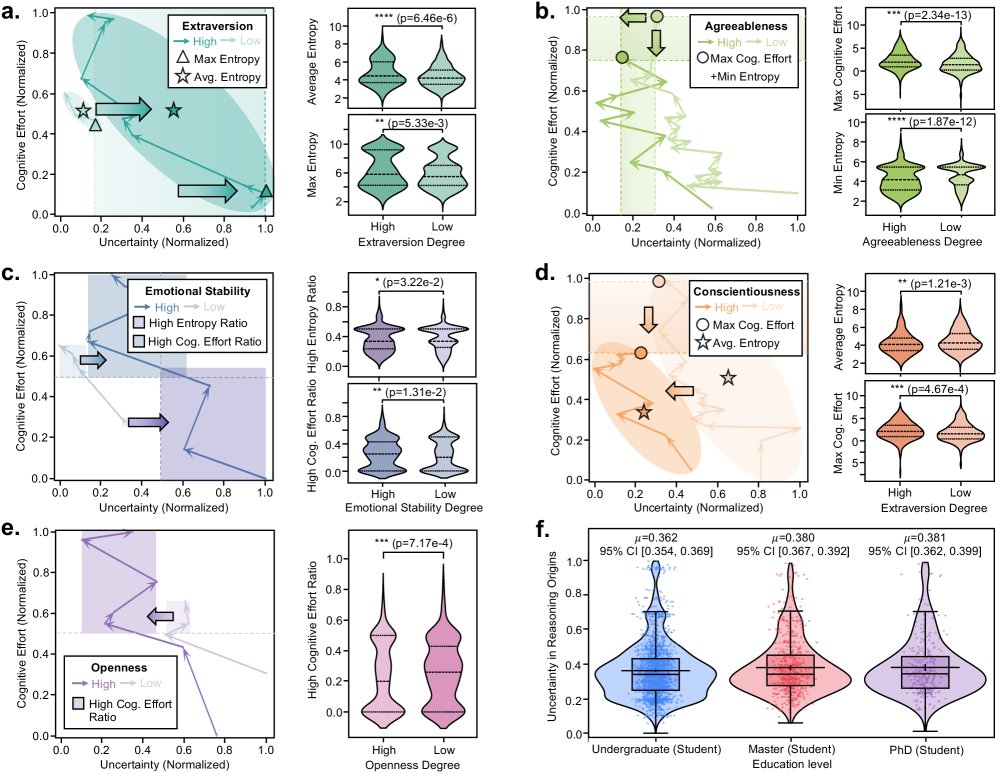
该框架能够量化不同个体在推理行为上的差异。

• 人格特质（大五人格）：
  • 外向性 (Extraversion) 高者偏好高不确定性的探索状态。
  • 宜人性 (Agreeableness) 高者倾向于更高效、确定性更高的推理路径。
  • 情绪稳定性 (Emotional Stability) 高者在高不确定性下仍能保持高效推理。
  • 尽责性 (Conscientiousness) 高者推理路径结构性强，不确定性较低。
  • 开放性 (Openness) 高者表现出更强的探索性，认知努力投入更多。
• 教育水平：教育程度更高（如博士）的参与者在推理初始阶段表现出更高的不确定性，这表明他们可能从更广阔的假设空间开始探索，对模糊性的容忍度更高。

在前沿心理学理论中的应用

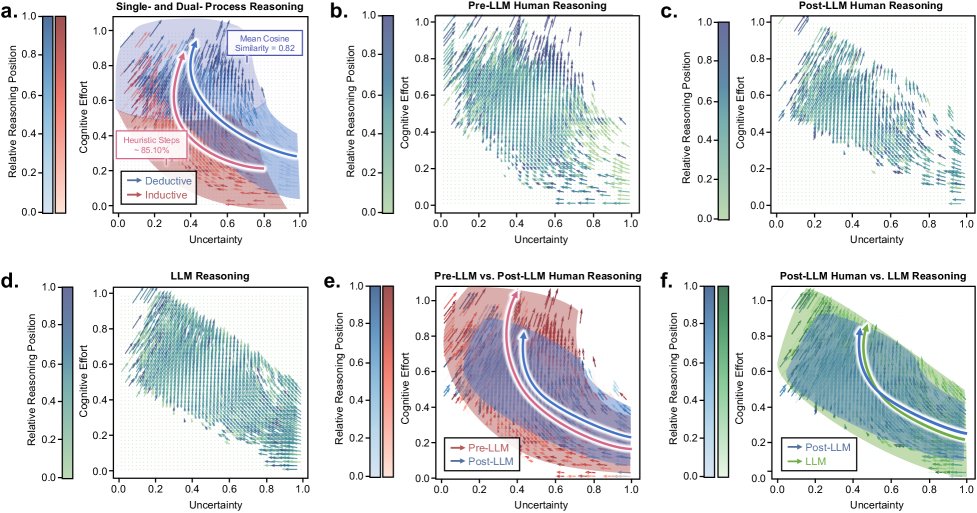
单/双过程理论之争

IFT为“推理是单一过程还是双过程”的长期争论提供了调和的视角。

• 局部上呈双过程：在单条推理轨迹内部，可以观察到从高不确定性、低努力的“直觉”区域到低不确定性、高努力的“分析”区域的转变，支持双过程理论。
• 全局上呈单过程：当汇总大量数据时，所有推理轨迹汇合成一个连续、平滑的宏观流，且不同推理类型在后期阶段轨迹高度重合，支持单一过程框架。 结论是，双过程效应是统一的单过程架构中出现的局部动态。

LLM时代人类推理的重塑

• LLM正在重塑人类推理模式：实验对比发现，在广泛使用LLM后，人类的推理模式发生了显著变化。传统的推理从低认知努力开始，逐步探索深入；而受LLM影响的推理则倾向于从一个较高的认知努力起点开始，但后期探索性努力减弱。
• 人类推理与LLM趋同：后LLM时代的人类推理轨迹与GPT-4o自身的轨迹高度重合。这表明，频繁使用LLM不仅改变了推理环境，也可能导致用户下意识地内化和模仿模型的推理模式，使得人机认知趋于一致。

总结

本文提出的IFT框架成功地将人类推理过程转化为一个可测量、可比较的动态系统。它不仅能够统一描述不同类型的推理，识别错误模式和个体差异，还有力地推动了对核心心理学理论（如单/双过程理论）的理解，并首次定量揭示了LLM对人类认知过程的深刻影响。这项工作为连接认知理论与经验测量搭建了一座桥梁，为未来研究人类乃至人工智能的认知架构提供了强大的新工具。