Towards a Unified View of Large Language Model Post-Training
-
ArXiv URL: http://arxiv.org/abs/2509.04419v1
-
作者: Ning Ding; Kaiyan Zhang; Hongyi Liu; Bowen Zhou; Xuekai Zhu; Zhekai Chen; Yuxin Zuo; Bingning Wang; Xingtai Lv; Youbang Sun
-
发布机构: Shanghai AI Laboratory; Tsinghua University; WeChat AI
TL;DR
本文提出了一个统一的策略梯度估计器（UPGE），将监督微调（SFT）和强化学习（RL）两种后训练范式归纳到单一的优化目标下，并基于此设计了一种名为混合后训练（HPT）的新算法，该算法能根据模型的实时表现动态地在SFT和RL之间切换，从而有效提升模型的推理能力。
关键定义
- 统一策略梯度估计器 (Unified Policy Gradient Estimator, UPGE)：本文提出的一个理论框架，旨在统一各种后训练算法（包括SFT和多种RL方法）的梯度计算。其核心思想是，这些方法的梯度都可以表示为一个通用形式：\(grad_Uni = 𝟙_stable * (1/π_ref) * Â * ∇π_θ\)。该估计器由四个可互换的部分组成：稳定掩码 \(𝟙_stable\)、参考策略分母 \(π_ref\)、优势估计 \(Â\) 和似然梯度 \(∇π_θ\)。不同的算法可以看作是这个统一框架下，对这四个部分采用不同选择的特例。
- 混合后训练 (Hybrid Post-Training, HPT)：基于UPGE理论提出的一种实用算法。该算法使用一个混合损失函数 \(L = α*L_RL + β*L_SFT\)，结合了强化学习损失和监督微调损失。其核心机制是，系数 \(α\) 和 \(β\) 是根据模型在特定问题上的实时采样表现动态决定的。当模型表现不佳时，算法侧重于SFT（利用高质量示范数据进行模仿学习）；当模型表现良好时，则切换到RL（鼓励探索）。
相关工作
目前，大型语言模型的后训练主要依赖两大范式：监督微调（Supervised Fine-Tuning, SFT）和强化学习（Reinforcement Learning, RL）。SFT通过在高质量的人工标注数据上进行训练，能高效地让模型对齐特定任务，但容易过拟合，限制了模型的探索和泛化能力。相反，RL允许模型在环境中自由探索并根据反馈进行学习，能提升推理能力，但直接应用于基础模型（即“Zero RL”）时，对于能力较弱的模型或复杂任务，可能因无法探索到有意义的奖励信号而失败。
为了结合两者的优点，业界主流范式是“先SFT后RL”（SFT-then-RL）的序列化流程，但这不仅资源消耗巨大，且调优过程复杂。近期一些工作尝试将SFT和RL的损失函数直接结合进行混合策略学习，但大多将两者视为独立的目标，缺乏一个统一的理论来解释为何这两种信号可以被有效结合。
本文旨在解决这一问题：为SFT和RL的结合提供一个统一的理论基础，阐明它们本质上是在优化同一个目标，并利用这一理论洞见设计一个更高效、更具原则性的动态混合训练算法。
本文方法
统一策略梯度估计器 (UPGE)
本文首先从理论上统一了SFT和RL。研究发现，尽管数学形式各异，但多种后训练算法的策略梯度计算可以被抽象为一个统一的框架，即统一策略梯度估计器（UPGE）。
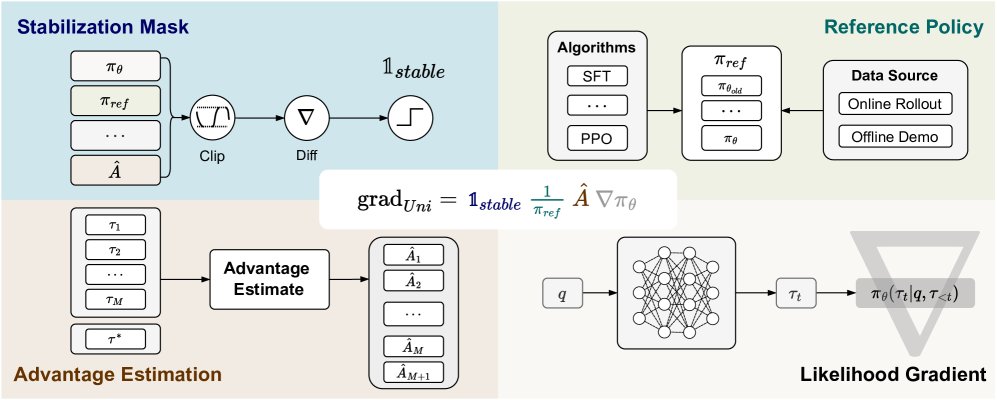图1：统一策略梯度估计器图示。似然梯度部分的背景“∇”符号指代对策略 \(π_θ\) 计算梯度。
创新点
本文的核心创新在于将后训练的梯度计算分解为四个可互换的模块，揭示了不同算法间的内在联系。
\[\text{grad}_{Uni} = \mathbb{1}_{stable} \frac{1}{\pi_{ref}} \hat{A} \nabla\pi_{\theta}\]这四个模块分别是：
- 稳定掩码 (Stabilization Mask) \(mathbb{1}_{stable}\)：源于PPO等算法的裁剪（clipping）操作，用于在模型更新过大时关闭梯度，以保证训练的稳定性。不同算法采用不同的掩码策略。
- 参考策略分母 (Reference Policy Denominator) \(π_{ref}\)：作为一个Token级别的重加权系数，通常是某个策略概率的倒数。例如，SFT使用当前策略 \(π_θ\)，而PPO风格的RL使用生成采样的旧策略 \(π_{θ_old}\)。离线数据方法由于无法获知采样策略，常假设 \(π_{ref}=1\)。
- 优势估计 (Advantage Estimate) \(Â\)：评估当前生成序列相对于平均水平的优劣。SFT可被视为所有示范序列的优势 \(Â\) 均为1的特例，而RL方法则使用不同的优势计算方式，如基于奖励的归一化值。
- 似然梯度 (Likelihood Gradient) \(∇π_θ(τ)\)：将目标函数的梯度信号反向传播到模型参数 \(θ\) 的通用部分，在所有算法中保持一致。
下表展示了多种经典算法如何被纳入UPGE框架。
| 算法 | 参考策略 \(π_ref\) | 优势估计 \(Â\) | 统一策略梯度估计器形式 |
|---|---|---|---|
| SFT | \(π_θ\) | \(Â_SFT ≡ 1\) | \(∇π_θ(τ) * (1 / π_θ(τ))\) |
| PPO | \(π_{θ_old}\) | GAE | \(∇π_θ(τ) * (Â_PPO * 𝟙_Clip / π_{θ_old}(τ))\) |
| GRPO | \(π_{θ_old}\) | Group-wise Normalization | \(∇π_θ(τ) * (Â_GRPO * 𝟙_Clip / π_{θ_old}(τ))\) |
| … | … | … | … |
优点
该统一视图的优点在于，它从一个共同目标 (Common Objective) 出发，证明了SFT和RL并非相互冲突，而是在优化同一个目标函数 \(J_μ(θ)\) 的不同部分：
\[\mathcal{J}_{\mu}(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}(\cdot \mid q)}[r(\tau \mid q)] - \mu \mathrm{KL}(\pi_{\beta}(\cdot \mid q) \ \mid \pi_{\theta}(\cdot \mid q))\]该目标旨在最大化期望奖励（RL项），同时保持与示范策略 \(π_β\) 的一致性（SFT项）。通过数学推导，该目标的梯度可以被分解为RL和SFT两个部分，两者都可以通过选择不同的UPGE组件来表示。这为动态组合SFT和RL提供了坚实的理论依据，并指出可以通过更优的组件选择来平衡不同梯度估计器的偏差-方差，从而改进后训练过程。
混合后训练 (HPT) 算法
基于UPGE的理论洞见，本文提出了HPT算法，旨在动态地选择更合适的训练信号。
算法设计
HPT采用了一个混合损失函数：
\[\mathcal{L} = \alpha \mathcal{L}_{\mathrm{RL}} + \beta \mathcal{L}_{\mathrm{SFT}}\]其关键在于系数 \(α\) 和 \(β\) 是动态的，由模型在当前问题 \(q\) 上的实时性能反馈决定。
具体流程如下：
- 性能评估：针对一个问题 \(q\)，模型生成 \(n\) 个轨迹（rollouts），并通过一个验证器（verifier）评估每个轨迹的正确性，得到一个奖励分数（0或1）。模型在该问题上的性能 \(P\) 定义为这 \(n\) 个分数的平均值。
-
动态切换：根据性能 \(P\) 和一个预设的阈值 \(γ\) 来确定 \(α\) 和 \(β\) 的值。
\[(\alpha, \beta) = \begin{cases} (0, 1), & \text{if } P \leq \gamma \\ (1, 0), & \text{if } P > \gamma \end{cases}\]- 当模型表现不佳 (\(P ≤ γ\)) 时，设置 \(α=0, β=1\)，此时算法退化为SFT，强制模型学习高质量的示范轨迹，实现有效利用（exploitation）。
- 当模型表现良好 (\(P > γ\)) 时，设置 \(α=1, β=0\)，此时算法切换为RL（本文实现中采用Dr. GRPO），鼓励模型进行探索（exploration）以发现更优的解法。
- 模型更新：使用计算出的混合损失 \(L\) 来更新模型参数。
该机制使HPT能够根据任务难度和模型自身能力自适应地平衡模仿学习和探索学习，避免了单纯SFT的过拟合和单纯RL在弱模型上的探索困境。
Algorithm 1 The Hybrid Post-Training (HPT) Algorithm
Input: 预训练LLM π_θ; SFT数据集 D_SFT; 验证器 v; 采样数 n; 总步数 T; 反馈函数 f, g; 学习率 η
Output: 微调后的策略 π_{θ*}
for t=1 to T do
for i=1 to n do
从 π_θ(·|q) 采样轨迹 τ_i
使用验证器评估奖励: v(τ_i) ← R(τ_i) ∈ {0,1}
end for
P ← (1/n) * Σ v(τ_i) # 计算模型在问题q上的性能
α ← f(P), β ← g(P) # 根据性能反馈获取系数
使用采样 {τ_i} 计算RL损失 L_RL
使用监督轨迹 τ* 计算SFT损失 L_SFT
L ← α * L_RL + β * L_SFT # 混合损失
θ ← θ - η * ∇_θ L
end for
return π_{θ*}
实验结论
关键结果
本文在多种模型（Qwen2.5-Math-1.5B/7B, LLaMA-3.1-8B）和多个数学推理基准（AIME, AMC, MATH等）上进行了广泛实验。
- 性能显著提升：HPT在所有实验设置中均一致地超越了各个基线方法，包括SFT、GRPO、顺序执行的SFT→GRPO，以及其他混合策略方法（如LUFFY和SRFT）。
- 在强模型上的优势：以Qwen2.5-Math-7B为例，HPT在AIME 2024基准上比最强的基线LUFFY高出6.9分，平均分高出2.9分。同时，在GPQA和ARC-c等分布外（OOD）数据集上也取得了最佳性能。
表2：Qwen2.5-Math-7B上HPT与基线的性能对比
| 模型 | AIME 24 | AMC | MATH-500 | Avg (ID) | ARC-c | GPQA | Avg (OOD) |
|---|---|---|---|---|---|---|---|
| Qwen2.5-Math-7B (Base) | 12.3 | 33.0 | 43.6 | 19.3 | 30.9 | 28.3 | 29.6 |
| SFT | 25.1 | 56.1 | 84.2 | 44.5 | 67.4 | 25.3 | 46.4 |
| GRPO | 19.4 | 59.1 | 81.8 | 43.1 | 81.2 | 36.4 | 58.8 |
| SFT → GRPO | 25.7 | 62.2 | 84.6 | 46.5 | 67.7 | 30.8 | 49.3 |
| LUFFY | 26.1 | 66.2 | 88.4 | 49.8 | 80.8 | 39.4 | 60.1 |
| HPT | 33.0 | 69.4 | 89.2 | 52.7 | 81.6 | 42.9 | 62.3 |
- 对不同模型和规模的通用性：HPT不仅在强大的数学模型上表现优异，在相对较弱或通用的模型（如LLaMA3.1-8B和Qwen2.5-Math-1.5B）上也取得了大幅性能提升，证明了其通用性。
表3：LLaMA3.1-8B 和 Qwen2.5-Math-1.5B 上的性能
| 模型 / 方法 | AIME 24 | AMC | MATH-500 | Avg |
|---|---|---|---|---|
| LLaMA3.1-8B | ||||
| LUFFY* | 1.9 | 13.5 | 39.0 | 13.2 |
| HPT | 2.1 | 18.6 | 47.8 | 18.2 |
| Qwen2.5-Math-1.5B | ||||
| SFT | 14.7 | 45.4 | 78.4 | 36.9 |
| LUFFY | 14.1 | 43.5 | 75.2 | 34.7 |
| HPT | 16.6 | 51.0 | 81.0 | 41.9 |
总结
实验结果有力地验证了HPT的有效性。其动态切换机制成功地结合了SFT的稳定学习和RL的有效探索，避免了在训练初期因模型能力不足而导致的无效探索，同时在模型能力提升后鼓励其发现新的、更优的解题路径。这使得HPT在各种场景下都能稳定地提升模型性能，尤其是在复杂的推理任务上。最终结论是，本文提出的统一理论框架（UPGE）为理解和设计后训练算法提供了新的视角，而基于该框架的HPT算法是一种比现有方法更高效、更具适应性的后训练策略。