Towards Flash Thinking via Decoupled Advantage Policy Optimization
-
ArXiv URL: http://arxiv.org/abs/2510.15374v1
-
作者: Xinhong Ma; Feng Zhang; Hang Gao
-
发布机构: Alibaba Inc.; Peking University
TL;DR
本文提出了一种名为DEPO的新型强化学习框架，它通过解耦高效与低效推理片段的优势计算、引入难度感知的长度惩罚和优势裁剪机制，在保持甚至提升模型准确率的同时，显著减少了大型推理模型的无效推理（“过度思考”）和响应长度。
关键定义
本文的核心在于对模型生成内容进行了精细的拆分和差异化处理，并为此定义了以下关键术语：
- 高效推理片段 (Efficient Segment): 在模型的思维链（Chain-of-Thought, CoT）中，从开始到首次推导出正确答案的部分。这部分被认为是解决问题的必要路径。
- 低效推理片段 (Inefficient Segment): 在得出正确答案之后，模型继续生成的冗余内容，如对正确答案的反复验证、自我反思或探索其他解法。这部分是“过度思考”的主要体现，也是本文优化的核心目标。
- DEPO (Decoupled Advantage Policy Optimization): 本文提出的解耦优势策略优化框架。它是一种强化学习算法，旨在通过对高效和低效推理片段应用不同的优化策略来减少模型的响应长度和冗余思考。
- GRM (Generative Reward Model): 一个经过微调的生成式奖励模型。在DEPO框架中，它的核心作用是精准地识别出思维链中首次得出正确答案的位置，从而实现对高效与低效推理片段的自动分割。
- 过度思考 (Overthinking): 指模型在解决问题时，尤其是在已经找到正确答案后，仍然产生大量冗长、重复或不必要的推理步骤的现象。这导致了推理延迟和计算成本的增加。
相关工作
当前，大型推理模型（Large Reasoning Models, LRMs）在数学、编程等复杂任务上取得了显著进展，这主要得益于长思维链（CoT）的应用。然而，一个突出的瓶颈是“过度思考”问题，即模型会生成大量冗长和冗余的推理路径，导致高昂的推理延迟和计算成本。
为了解决这个问题，领域内的现有方法主要分为三类：
- 基于长度的偏好数据: 通过人工标注或规则为不同长度的回答构建偏好数据集进行训练。这种方法成本高昂且可能存在偏好不匹配的问题。
- 在奖励中加入长度惩罚: 在奖励函数中直接对长度进行惩罚，鼓励模型生成更简洁的回答。但这种方法将整个回答作为一个整体，无法区分并针对性地抑制冗余的推理部分，并且可能扭曲对单个token的优势估计，导致策略更新方向错误，损害模型准确性。
- 提取有效Token: 提取思维链中的有效部分，并降低无效部分的优势值权重。但这种方法仅依赖有效与无效片段的长度比例来调整优势，未考虑低效片段中具体的“过度思考”程度，因此模型难以学会有效抑制特定的过度思考模式。
本文旨在解决上述方法的局限性，通过显式地将模型回答划分为高效和低效部分，精准地抑制低效片段中的过度思考，同时降低整体回答长度，且无需构建昂贵的偏好数据集。
本文方法
本文提出了DEPO (Decoupled Advantage Policy Optimization)，一个创新的强化学习算法，旨在通过识别并抑制冗余推理来缓解模型的“过度思考”问题。该方法包含三个核心组件：解耦优势计算、难度感知的长度惩罚和优势裁剪。
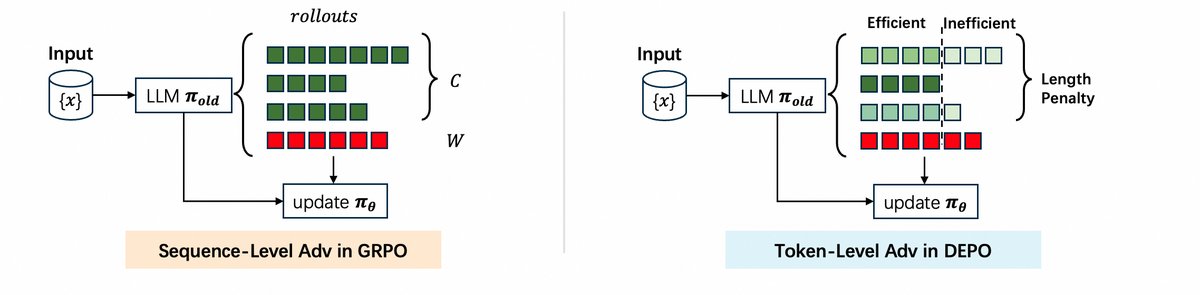上图展示了DEPO与传统序列级方法的区别，DEPO能够实现token级别的优势估计，从而将策略$\pi_{old}$更新为更高效的$\pi_{\theta}$。
算法流程
DEPO的整体算法流程如下：
- 采样: 对于每个问题，使用当前策略模型批量生成多个回答。
- 奖励计算: 计算每个回答的准确率奖励和长度奖励。
- 优势计算与裁剪: 计算序列级别的优势值，并通过优势裁剪避免错误的优化方向。
- 解耦与token级优势: 使用GRM识别正确回答中的低效推理片段，量化其冗余度，并据此对这些token的优势值进行降权，实现解耦。
- 策略更新: 基于token级别的优势值，使用PPO损失函数更新策略模型。
创新点
解耦优势计算 (Decoupled Advantage)
这是DEPO的核心创新。该方法旨在让模型主要从高效推理中学习，同时抑制冗余部分。
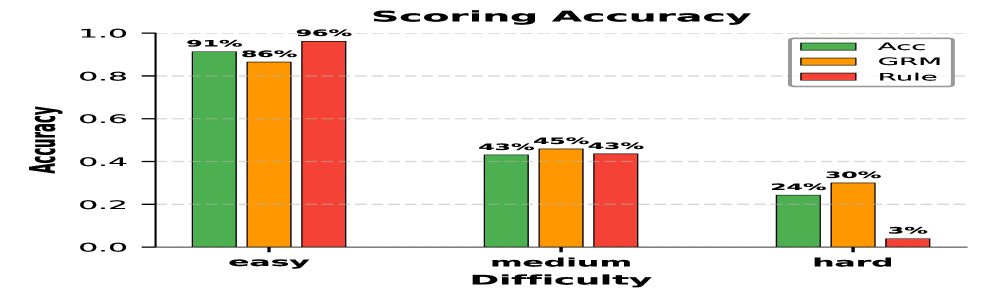
首先，本文微调了一个GRM (Generative Reward Model)，用于准确识别推理过程中首次得出正确答案的句子。实验证明，GRM在判定回答正确性方面，尤其是在复杂问题上，显著优于传统的基于规则的方法。
然后，本文定义了一种量化低效片段 $o_{ie}$ 中冗余推理步骤的方法。通过匹配预定义的冗余模式（如“让我们再检查一遍”等过渡短语和自我反思词汇）来计算冗余度$K$。
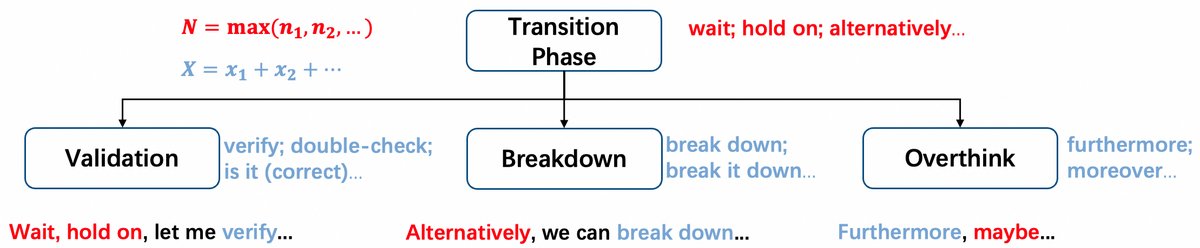
冗余推理步骤数 $K$ 的计算公式为：
\[K = \text{max}(N, X)\]其中，$N$是开启另一条推理路径的过渡短语的最大数量，$X$是自我反思词汇的总数。
最后，将序列级优势 $\hat{A}_{i}$ 转换为token级优势 $\hat{A}_{i,t}$。对于低效片段 $o_{ie}$ 中的token，其优势值会被一个衰减函数 $f(\cdot)$ 降权：
\[\hat{A}_{i,t}=\begin{cases}f(o_{ie})\cdot\hat{A}_{i},&\text{if }y_{t}\text{ in }o_{ie}\text{ and }o_{i}\text{ is correct}\\ \hat{A}_{i},&\text{otherwise}\end{cases}\]衰减函数 $f(\cdot)$ 定义为：
\[f(\cdot)=1-\beta\cdot(1-e^{-\beta\cdot K})\]其中 $\beta$ 是超参数。$K$越大，衰减越强，从而在梯度更新时抑制了这些冗余token的贡献。最终的优化目标函数为：
\[\mathcal{J}_{\text{DEPO}}(\theta)=\mathbb{E}_{x\sim D,\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{\text{old}}}(\cdot \mid x)}\bigg[\frac{1}{\sum_{i=1}^{G} \mid o_{i}^{\prime} \mid }\sum_{i=1}^{G}\sum_{t=1}^{ \mid o_{i}^{\prime} \mid }\Bigg\{\min\bigg[\frac{\pi_{\theta}}{\pi_{\text{old}}}\cdot\hat{A}_{i,t},\,\text{clip}(\frac{\pi_{\theta}}{\pi_{\text{old}}},1\!-\!\epsilon,1\!+\!\epsilon)\cdot\hat{A}_{i,t}\bigg]\Bigg\}\bigg]\]难度感知的长度惩罚 (Difficulty-Aware Length Penalty)
为了降低模型回答的整体长度，本文设计了一种与问题难度相关的长度惩罚机制。
首先，定义了准确率奖励 \(R_accuracy\)，对超长回答给予-1的惩罚，视其为比错误回答更严重的问题。
\[R_{\text{accuracy}}(o_{i}\mid x)=\begin{cases}1,&\text{if }o_{i}\text{ is correct}\\ 0,&\text{if }o_{i}\text{ is incorrect}\\ -1,&\text{if }o_{i}\text{ is overlong}\end{cases}\]其次，引入了长度奖励 \(R_length\)，该奖励的大小与正确回答的长度方差以及问题的难度（用一批采样中正确回答的数量 $\delta$ 来衡量）相关。对于简单问题（$\delta$ 较大），长度惩罚更强。
\[R_{\text{length}}(o_{i}\mid x)=\begin{cases}-\alpha\cdot(1-e^{-\alpha\cdot\delta})\cdot\frac{\mid o_{i}\mid-\text{mean(}l_{\text{pos}}\text{)}}{\text{std(}l_{\text{pos}}\text{)}},&\text{if }o_{i}\text{ is correct}\\ 0,&\text{if }o_{i}\text{ is incorrect}\end{cases}\]最终的总奖励是两者的和：
\[R(o_{i}\mid x)=R_{\text{accuracy}}(o_{i}\mid x)+R_{\text{length}}(o_{i}\mid x)\]优势裁剪 (Advantage Clipping)
长度惩罚机制可能导致优势估计出现偏差，例如，一个正确但冗长的回答可能获得负的优势值，而一个错误的回答在与超长回答对比时可能获得正的优势值。这会误导策略更新。
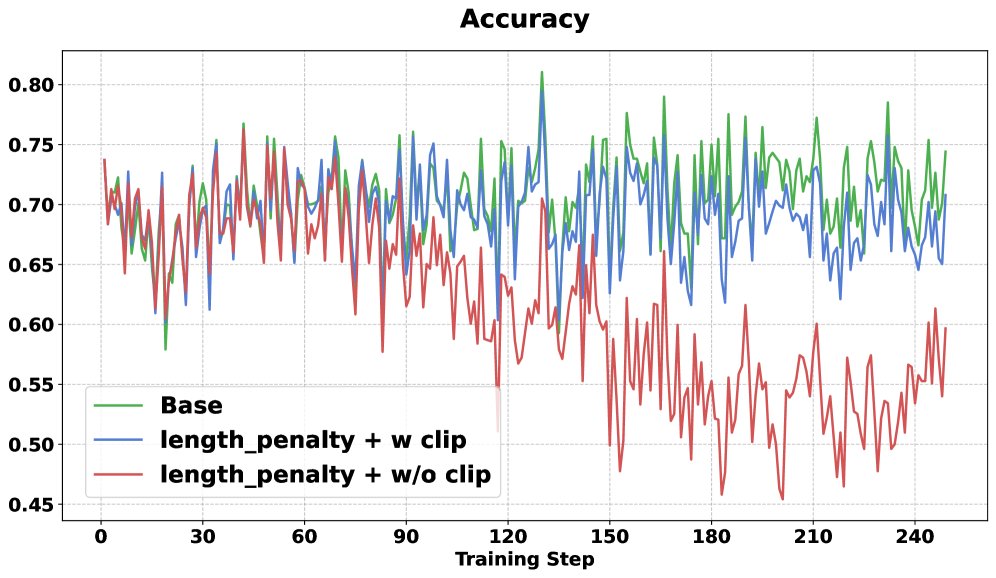
为解决此问题，本文提出了一种优势裁剪方法，确保正确回答的优势值始终为正，而错误回答的优势值始终为负。
\[\hat{A}_{i}=\begin{cases}\text{clip}(\hat{A}_{i}^{\prime},\text{min}(\hat{A}_{\text{pos}}^{\prime}),+\infty),&\text{if }o_{i}\text{ is correct}\\ \text{clip}(\hat{A}_{i}^{\prime},-\infty,0),&\text{if }o_{i}\text{ is incorrect}\end{cases}\]其中 $\hat{A}_{i}^{\prime}$ 是原始优势值，$\text{min}(\hat{A}_{\text{pos}}^{\prime})$ 是所有正确回答的原始优势值中的最小值。这种裁剪策略保证了梯度更新方向的正确性。
实验结论
实验设置
- 基础模型: DeepSeek-R1-Distill-Qwen-7B 和 DeepSeek-R1-Distill-Qwen-1.5B。
- 训练与测试数据: 使用DeepScaleR数学数据集进行训练，并在AIME24/25, AMC23, MATH500等多个数学基准上进行评测。
- GRM: 使用Qwen2.5-Instruct-7B模型通过监督微调得到。
- 基线方法: 与原始模型、GRPO、DAST、LC_R1、GRPO-Lead等方法在准确率和响应长度上进行对比。
主要结果
如下表所示，DEPO在多个数据集上取得了显著效果。
| 方法 | AIME24(Acc/Len) | AIME25(Acc/Len) | AMC23(Acc/Len) | MATH500(Acc/Len) | 平均(Acc/Len) |
|---|---|---|---|---|---|
| DeepSeek-R1-Distill-Qwen-7B | |||||
| Original | 50.6 / 10640 | 36.5 / 11090 | 85.3 / 6850 | 94.3 / 4680 | 69.2 / 8315 |
| GRPO | 53.6 / 11130 | 38.6 / 11782 | 86.8 / 7410 | 94.5 / 5012 | 70.9 / 8834 |
| DAST | 50.7 / 7650 | 38.0 / 8000 | 85.4 / 4300 | 92.5 / 3100 | 69.2 / 5763 |
| LC_R1 | 48.6 / 7132 | 34.3 / 7453 | 86.5 / 3840 | 93.9 / 2810 | 68.3 / 5309 |
| GRPO-Lead | 53.0 / 6980 | 37.9 / 7500 | 86.6 / 3450 | 93.8 / 2620 | 70.3 / 5138 |
| DEPO | 51.2 / 6561 | 39.6 / 7111 | 88.4 / 3721 | 95.6 / 2953 | 71.2 / 5087 |
| DeepSeek-R1-Distill-Qwen-1.5B | |||||
| Original | 39.5 / 9910 | 25.1 / 10321 | 75.3 / 6100 | 84.4 / 4500 | 58.6 / 7708 |
| GRPO | 41.5 / 10500 | 26.9 / 11200 | 78.4 / 6400 | 86.8 / 4800 | 60.9 / 8225 |
| DEPO | 41.7 / 6061 | 27.3 / 6598 | 80.8 / 3123 | 88.6 / 2894 | 62.1 / 4669 |
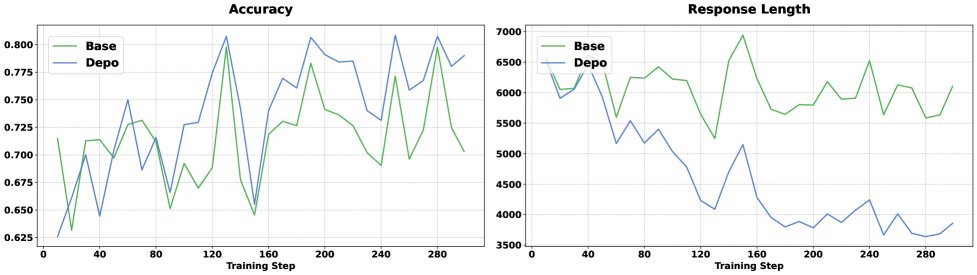
- 长度显著缩短: 对于7B模型，DEPO在保持甚至平均提升2.0%准确率的同时，将响应长度平均减少了38.7%。对于1.5B模型，长度减少了39.1%，准确率也比基础模型高2.1%。
- 性能权衡: 在简单任务（AMC23, MATH500）上，DEPO取得了最高的准确率和次优的长度效率。在困难任务（AIME24, AIME25）上，DEPO在长度上大幅领先，准确率与原始模型持平或略有提升，表现稳定。
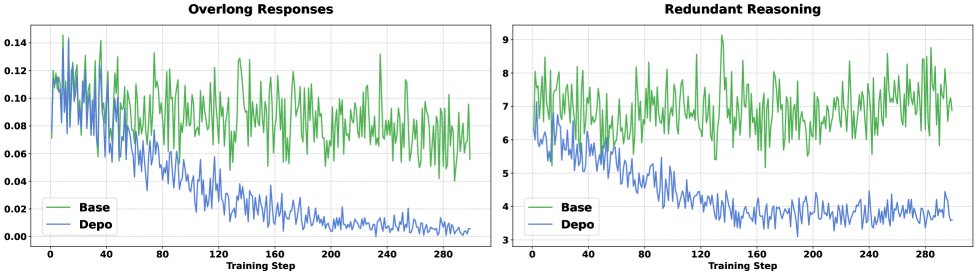
- 抑制超长回答与冗余推理: 实验分析表明，DEPO将因重复验证导致的超长回答比例从10.7%降至0.1%，并将低效片段中的冗余推理步骤减少了约50%。
消融研究
消融实验验证了DEPO各组件的有效性。
| 方法 | AIME24(Acc/Len/Reflect) | AIME25(Acc/Len/Reflect) | AMC23(Acc/Len/Reflect) | MATH500(Acc/Len/Reflect) | 平均(Acc/Len/Reflect) |
|---|---|---|---|---|---|
| DEPO | 51.2 / 6561 / 5.2 | 39.6 / 7111 / 5.5 | 88.4 / 3721 / 2.3 | 95.6 / 2953 / 1.7 | 71.2 / 5087 / 3.5 |
| -w/o Adv-Decouple | 50.4 / 7002 / 6.8 | 37.7 / 7300 / 7.3 | 86.6 / 3450 / 2.8 | 93.8 / 2620 / 3.1 | 68.9 / 4944 / 4.8 |
| -w/o Len-Penalty | 52.1 / 6962 / 5.1 | 38.8 / 7638 / 5.4 | 88.4 / 3721 / 2.0 | 94.4 / 2953 / 1.7 | 70.3 / 5174 / 3.6 |
- 长度惩罚 (Len-Penalty): 在降低响应长度方面更有效，但单独使用会轻微损害准确率。
- 解耦优势 (Adv-Decouple): 在抑制特定冗余推理行为（如“double-check”）和提升模型准确率方面更有效。
- 总结: 两个组件共同作用，实现了长度和准确率之间的最佳平衡。解耦优势是提升准确率和抑制自我反思的关键，而长度惩罚则确保了整体的简洁性。
最终结论
本文提出的DEPO框架通过一种创新的解耦优势机制，成功地让模型学会区分并抑制低效的推理步骤。结合难度感知的长度惩罚和优势裁剪，DEPO在不牺牲甚至提升任务准确率的前提下，显著缩短了模型的响应长度，有效缓解了“过度思考”问题，为训练更高效的推理模型提供了新的方向。