Towards Unbiased Calibration using Meta-Regularization
-
ArXiv URL: http://arxiv.org/abs/2303.15057v3
-
作者: F. Gilardi; M. Kubli; Meysam Alizadeh
-
发布机构: Amazon
TL;DR
本文提出了一种名为元正则化 (Meta-Regularization) 的新方法，通过一个元学习框架来学习无偏的、校准良好的深度学习模型。该方法包含两个核心组件：一个能为Focal Loss学习样本级连续 \($\gamma\)$ 值的 \($\gamma$-Net\)，以及一个作为无偏、可微校准目标的平滑期望校准误差 (SECE)。
关键定义
本文提出了以下几个核心概念：
- 元正则化 (Meta-Regularization): 一种双层优化框架。内层循环使用由元网络（\($\gamma$-Net\)）提供的正则化参数（即\($\gamma\)$值）来优化主干网络的预测性能；外层循环则使用一个独立的校准损失（SECE）在验证集上优化元网络的参数，从而间接引导主干网络向更好的校准方向学习。
- $\gamma$-网络 ($\gamma$-Net): 一个元学习器，其结构是一个小型神经网络。它接收主干网络倒数第二层的特征表示作为输入，并为每个样本输出一个连续的、特定的\($\gamma\)$值。这个\($\gamma\)$值被用于Focal Loss中，以实现对每个样本的精细化正则。
- 平滑期望校准误差 (Smooth Expected Calibration Error, SECE): 一种基于高斯核的、可微的、无偏的期望校准误差（ECE）代理指标。它通过核函数在置信度空间中对邻近样本的准确率进行加权平均，以“平滑”地估计每个点的“软准确率”，从而避免了传统ECE计算中因离散分箱（binning）而引入的偏差。
相关工作
现代深度神经网络（DNNs）虽然在预测精度上表现出色，但普遍存在校准不佳的问题，即其输出的置信度不能准确反映真实的可能性，常常表现为过度自信或自信不足。
当前解决此问题的方法主要分为几类：
- 后处理方法 (Post-hoc Methods): 如温度缩放 (Temperature Scaling, TS)，在模型训练后对输出概率进行校正。
- 正则化方法 (Regularization Methods): 在训练中隐式地引导模型提升校准性，如标签平滑 (Label Smoothing, LS)、Mix-up训练，以及将Focal Loss用作熵正则化器。
- 可微代理指标: 开发ECE的可微版本，如MMCE和DECE，并将其作为损失函数的一部分直接优化。
然而，这些方法存在瓶颈：
- 依赖分箱的校准指标（如ECE）会引入偏差，其评估结果受分箱数量和方式的影响。
- Focal Loss等方法通常使用全局固定或按周期调整的\($\gamma\)$值，这种“一刀切”的正则化对于不同难度的样本可能不是最优的。
本文旨在解决上述问题，通过学习样本级的正则化强度并使用一种无偏的校准指标进行优化，来获得校准性更好且对评估方案更鲁棒的模型。
本文方法
本文提出的元正则化方法框架如下图所示，主要包括 \($\gamma$-Net\) 和 SECE 两大创新。
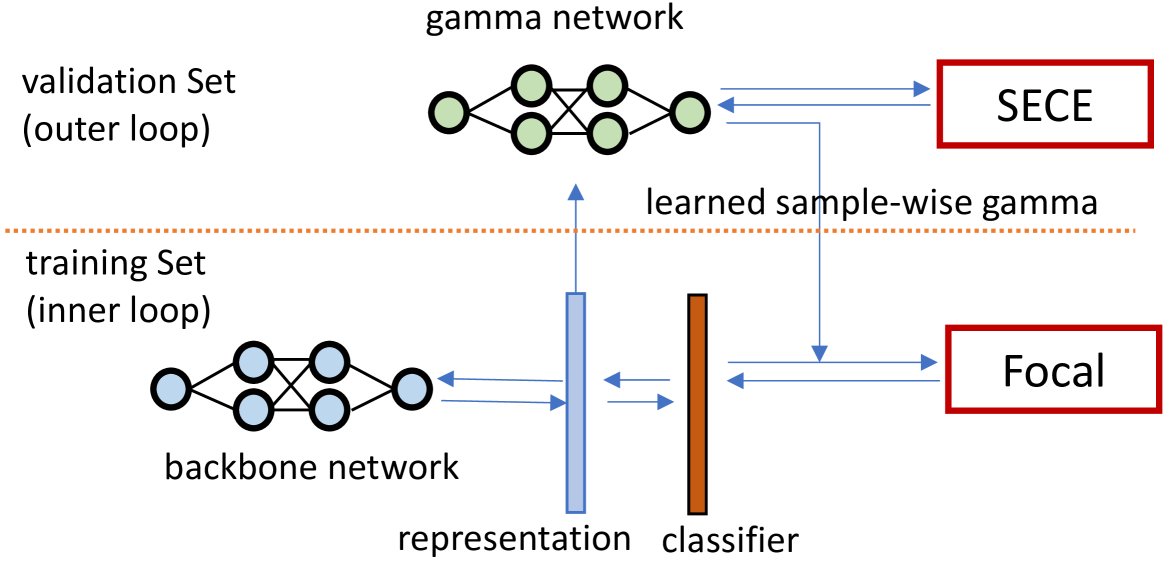图 1: 本文提出的通过元正则化提升模型校准的方法。内层循环使用Focal Loss优化主干网络，其\($\gamma\)$值由外层循环的\($\gamma$-Net\)提供。\($\gamma$-Net\)则通过本文提出的无偏、可微校准指标SECE进行优化。
整体优化框架
本文采用元学习的思想，将训练过程分为两个交替进行的循环：
- 内层循环（主干网络优化）: 使用一个训练小批量数据 $D_{train}$，通过带有样本级\($\gamma\)$值的Focal Loss来优化主干网络（如ResNet）的参数\($\theta\)$。此处的\($\gamma\)$由\($\gamma$-Net\)根据当前样本的特征预测得出。
- 外层循环（元网络优化）: 使用一个验证小批量数据 $D_{val}$，计算主干网络在该批数据上的SECE损失，并用此损失来优化\($\gamma$-Net\)的参数\($\phi\)$。
整体优化目标可以表示为：
\[\arg\min_{\theta,\phi}~{}\mathcal{L}(\theta,\phi,D_{train},D_{val})=\mathcal{L}_{FL_{\gamma}}(\theta,D_{train})+\mathcal{L}_{SECE}(\phi,D_{val})\]$\gamma$-Net: 学习样本级 Gamma
与传统Focal Loss使用固定的\($\gamma\)$值不同，本文设计了一个\($\gamma$-Net\)来为每个样本动态地生成一个最合适的\($\gamma\)$值。
\($\gamma$-Net\)的输入是主干网络倒数第二层的特征表示 $\mathbf{x}\in\mathbb{R}^{b\times d}$（$b$为批量大小，$d$为特征维度）。其计算过程如下：
- 首先通过一个 $k$ 头自注意力机制处理特征：
- 然后将注意力加权后的结果通过一个全连接层，生成样本级的\($\gamma\)$值：
其中，$\mathbf{A}$ 是注意力头矩阵，$\mathbf{W}$ 是全连接层权重，$\tau$ 是一个温度超参数，绝对值操作确保\($\gamma\)$为正。
创新点:
- 粒度: 实现了最精细的样本级（sample-wise）\($\gamma\)$值学习。
- 连续性: \($\gamma\)$是作为连续变量学习得到的，而非离散预设值，这为模型提供了更大的正则化灵活性。
SECE: 平滑期望校准误差
传统ECE依赖于离散的分箱，这不仅使其不可微，还引入了对分箱策略敏感的偏差。为了解决这个问题，本文提出了SECE。
核心思想: SECE的核心思想是，对于单个样本$x_i$，其所在置信度区间的“真实准确率”可以通过其邻近样本的准确率的加权平均来平滑地估计，权重由样本间在置信度空间中的距离决定。
计算方法:
-
软准确率估计 (Soft Accuracy, SACC): 对每个样本$i$，其软准确率$\text{SACC~{}}(b_i)$定义为所有样本$j$的真实准确率（0或1）的加权和，权重由高斯核函数 $K$ 给出：
\[\text{SACC~{}}(b_{i})=\sum_{j}^{M}\pi(x_{i})K(z_{i},z_{j})\]其中，$z_i$是样本$i$的置信度，$\pi(x_i)$是样本$i$的真实准确率（即$\mathbf{1}(\hat{y}_{i}=y_{i})$），$K(z_i, z_j)$是衡量置信度$z_i$和$z_j$相似度的高斯核函数：
\[K\left(x_{i},x_{j}^{\prime}\right)=\exp\left(-\frac{\left\ \mid x_{i} -x_{j}^{\prime}\right\ \mid ^{2}}{2h^{2}}\right)\]$h$是核的带宽。
-
SECE计算: SECE定义为所有样本的软准确率与置信度之差的绝对值的平均值：
\[\text{SECE~{}}=\frac{1}{M}\sum_{i}^{M} \mid \textrm{SACC~{}}(i)-\textsc{conf}(i) \mid\]
优点:
- 可微性: 由于高斯核是可微的，SECE也是可微的，因此可以作为损失函数直接用于梯度优化。
- 无偏性: SECE通过连续的核密度估计代替离散分箱，避免了分箱引入的偏差，比DECE等方法更稳定、鲁棒。
- 高效性: SECE通过简单的求和运算实现，比需要网络来预测分箱分配的DECE更高效。
实验结论
本文在CIFAR-10、CIFAR-100和Tiny-ImageNet三个数据集上进行了广泛实验。
性能对比
如下表所示，本文提出的方法 FLγ-SECE 在保持有竞争力的预测性能（测试错误率）的同时，在多个校准指标（NLL, ECE, MCE, ACE, Classwise ECE）上均取得了显著优于基线方法（包括CE, TS, Focal, FLSD, LS, Mixup, MMCE以及元学习基线CE-DECE）的效果。
- 校准性能: FLγ-SECE在所有数据集上都获得了最低或接近最低的校准误差。特别是在衡量最差情况偏差的MCE指标上，相较于元学习基线CE-DECE，在三个数据集上分别提升了18.62%、15.09%和9.41%。
- 预测性能: 相比其他以提升校准性为目标的正则化方法，本文方法对预测精度的影响较小。
表1：不同方法在CIFAR-10、CIFAR-100和Tiny-ImageNet上的性能对比
| 方法 | Error | NLL | ECE | MCE | ACE | Classwise ECE |
|---|---|---|---|---|---|---|
| CIFAR 10 | ||||||
| CE | 4.812 | 0.335 | 4.056 | 33.932 | 4.022 | 0.848 |
| CE (TS) | 4.812 | 0.211 | 3.083 | 26.695 | 3.046 | 0.656 |
| Focal | 4.874 | 0.207 | 3.193 | 28.034 | 3.174 | 0.690 |
| CE-DECE | 5.194 | 0.301 | 4.106 | 41.346 | 4.088 | 0.868 |
| FLγ-DECE | 5.434 | 0.193 | 2.257 | 56.633 | 2.396 | 0.557 |
| FLγ-SECE | 5.428 | 0.193 | 2.138 | 22.725 | 2.357 | 0.556 |
| CIFAR-100 | ||||||
| CE | 22.570 | 0.997 | 8.380 | 23.250 | 8.347 | 0.233 |
| CE (TS) | 22.570 | 0.959 | 5.388 | 13.454 | 5.360 | 0.208 |
| Focal | 22.498 | 0.900 | 5.044 | 12.454 | 5.015 | 0.203 |
| CE-DECE | 23.406 | 1.148 | 7.309 | 22.565 | 7.253 | 0.241 |
| FLγ-DECE | 23.712 | 0.888 | 1.879 | 8.271 | 1.838 | 0.195 |
| FLγ-SECE | 23.686 | 0.877 | 1.940 | 7.480 | 1.939 | 0.192 |
| Tiny-ImageNet | ||||||
| CE | 40.110 | 1.838 | 8.059 | 15.73 | 8.006 | 0.154 |
| Focal | 39.415 | 1.896 | 7.600 | 13.771 | 7.469 | 0.152 |
| CE-DECE | 41.350 | 2.228 | 10.694 | 20.888 | 10.553 | 0.160 |
| FLγ-DECE | 40.625 | 1.826 | 5.944 | 11.542 | 6.077 | 0.155 |
| FLγ-SECE | 40.850 | 1.829 | 5.794 | 11.477 | 5.848 | 0.156 |
注：仅展示部分基线和本文方法相关的结果，以突出对比。
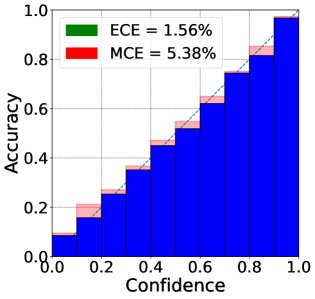图 2: （j）FLγ-SECE在CIFAR-100上的可靠性图。相比其他方法，该方法的置信度与准确率更为贴近对角线，表明校准性更好。
消融研究与分析
\($\gamma$-Net\)的有效性
实验观察到，在训练过程中，\($\gamma$-Net\)输出的\($\gamma\)$值的均值和标准差会动态变化。训练后期，\($\gamma\)$值的标准差增大，表明\($\gamma$-Net\)为不同样本学会了不同的\($\gamma\)$值，体现了其自适应正则化的灵活性。
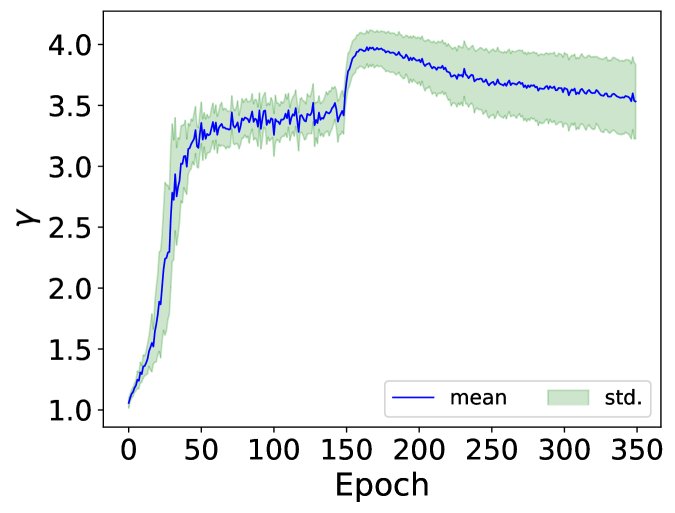图 3 (d): 在CIFAR-100上，测试集样本的平均\($\gamma\)$值及其标准差随训练周期的变化。标准差的增加表明\($\gamma$-Net\)学会了为不同样本分配不同的\($\gamma\)值。
SECE的鲁棒性
为了验证SECE在减少分箱偏差上的作用，实验比较了不同方法在ECE评估分箱数从10增加到1000时的表现。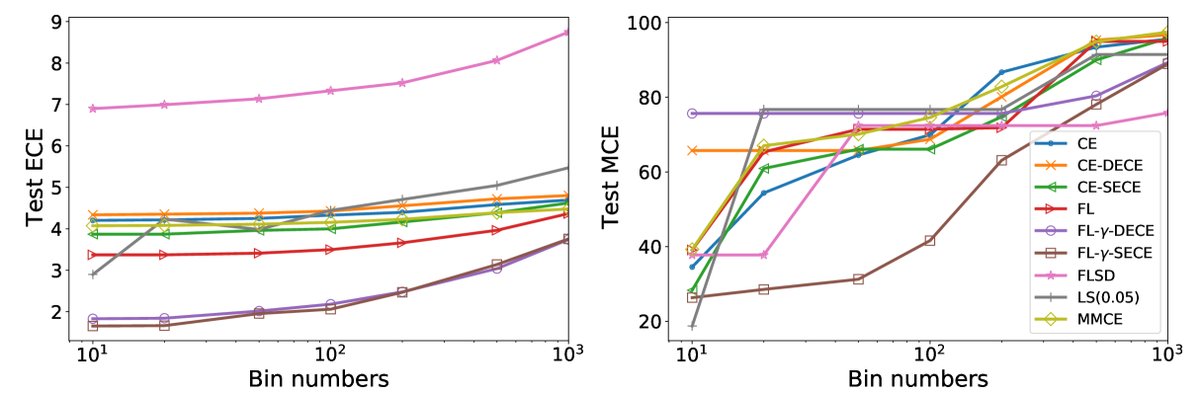
图 5: 在CIFAR-10上，随着评估时分箱数的增加，不同方法的ECE和MCE变化。FLγ-SECE（蓝色实线）在ECE和MCE上均表现出最低的增长和最优的稳定性，证明其训练出的模型对分箱机制具有很强的鲁棒性。
结果显示，基于\($\gamma$-Net\)的方法（特别是FLγ-SECE）在不同分箱数下都能保持较低的ECE和MCE，证明了SECE作为优化目标可以有效训练出对评估偏差鲁棒的校准模型。
最终结论
实验结果有力地证明：
- 通过\($\gamma$-Net\)学习样本级的连续\($\gamma\)$值，能有效提升模型的校准性能。
- SECE作为一个无偏、平滑的优化目标，不仅能稳定地引导\($\gamma$-Net\)的学习，还能显著降低由分箱机制引入的校准偏差，使模型在最差情况下的校准误差（MCE）更低。
- \($\gamma$-Net\)和SECE的结合（FLγ-SECE）在多个数据集和校准指标上均取得了SOTA或极具竞争力的表现，是实现深度模型无偏校准的一种有效途径。