Train for Truth, Keep the Skills: Binary Retrieval-Augmented Reward Mitigates Hallucinations

ArXiv URL: http://arxiv.org/abs/2510.17733v1
作者: Akari Asai; Faeze Brahman; Luke Zettlemoyer; Tong Chen; Hannaneh Hajishirzi
发布机构: Allen Institute for AI; Carnegie Mellon University; University of Washington

TL;DR

本文提出了一种名为“二元检索增强奖励 (Binary Retrieval-Augmented Reward, Binary RAR)”的在线强化学习方法，通过一个简单的二元（事实完全正确为1，否则为0）奖励信号，在不损害模型通用能力的前提下，显著减少了语言模型的幻觉。

关键定义

外在幻觉 (Extrinsic Hallucination)：指模型生成的输出内容无法通过其训练数据进行验证，即看似合理但事实错误的信息。本文主要关注并旨在缓解此类幻觉。
二元检索增强奖励 (Binary Retrieval-Augmented Reward, Binary RAR)：本文提出的核心奖励机制。它是一个二元信号 $r \in {0, 1}$，仅当模型的全部输出内容与检索到的文档证据完全一致、无任何矛盾时，奖励 $r=1$；否则，只要存在任何事实不符之处，奖励即为 $r=0$。
幻觉-效用权衡 (Hallucination-Utility Tradeoff)：指在缓解模型幻觉的过程中，常常会牺牲其通用能力（效用），例如生成内容的丰富性、遵循指令的能力、推理或编码能力等。本文的核心目标就是解决这一权衡问题。

本文方法

本文提出了一种基于在线强化学习 (online RL) 和新颖的 二元检索增强奖励 (Binary RAR) 的方法来解决幻觉-效用权衡问题。其核心框架如下图所示。

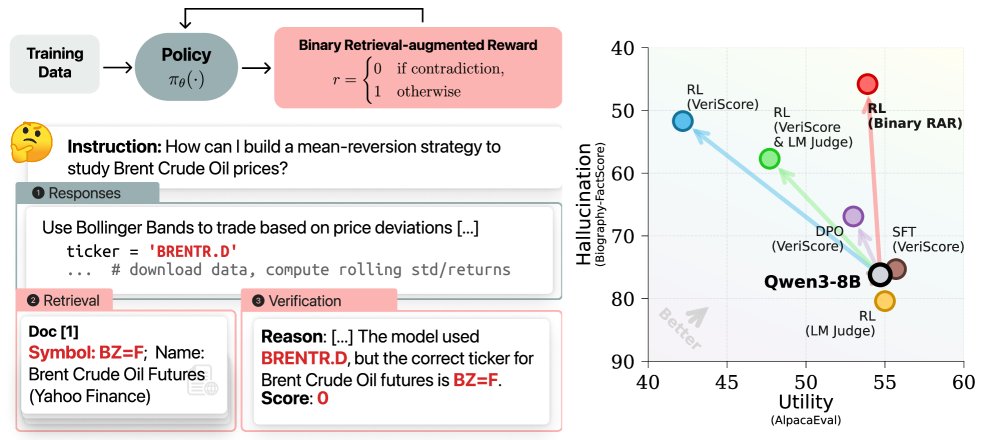Binary RAR 概览左图：使用 Binary RAR 的强化学习流程，根据检索验证的事实正确性分配二元奖励。右图：在所有后训练基线方法中，Binary RAR 在幻觉-效用权衡上表现最佳。

核心思想与训练目标

本文采用在线强化学习，即在训练过程中根据模型当前策略生成的样本（rollouts）来计算奖励并进行优化，而不是依赖固定的离线数据集。训练目标是最大化奖励函数 $r(x,y)$，同时通过KL散度 (Kullback–Leibler divergence) 惩罚项来防止模型偏离其原始能力太远。

其优化目标可以形式化地表示为：

\[\max_{\pi_{\theta}} \mathbb{E}_{\begin{subarray}{c}x\sim\mathcal{D}\\ y\sim\pi_{\theta}(\cdot\mid x)\end{subarray}}\Big[\,r(x,y)-\beta\,\mathbb{D}_{\mathrm{KL}}\!\big(\pi_{\theta}(\cdot\mid x)\;\ \mid \;\pi_{\mathrm{ref}}(\cdot\mid x)\big)\,\Big]\]

其中，$x$ 是输入提示， $y$ 是模型生成的响应，$\pi_{\theta}$ 是待优化的模型策略，$\pi_{\text{ref}}$ 是参考模型（通常是原始模型），$r(x,y)$ 是奖励函数，$\beta$ 是控制KL惩罚强度的系数。本文采用 Group Relative Policy Optimization (GRPO) 算法进行优化。

创新点：二元检索增强奖励 (Binary RAR)

本文最核心的创新在于奖励函数的设计。不同于以往使用连续分数（如事实正确率）作为奖励，本文提出了一种简单而严格的二元奖励信号。

奖励流程:

检索 (Retrieve)：对于模型生成的每个回答 $y$，从一个可靠的文档数据存储（如网页）中检索出最相关的 $k$ 份文档作为证据 $C(x,y)$。
验证 (Verify)：使用一个强大的语言模型作为验证器 (Verifier)，判断回答 $y$ 与证据 $C(x,y)$ 之间是否存在任何矛盾。值得注意的是，该验证过程是整体性的，无需将回答分解为多个原子声明，从而提升了效率。
奖励分配 (Reward Assignment)：根据验证结果分配奖励：
\[r(x,y)=\begin{cases}1&\text{如果回答 }(x,y)\text{ 与证据 }C(x,y)\text{ 之间没有发现矛盾,}\\ 0&\text{其他情况.}\end{cases}\]

优点

这种设计的核心优点包括：

抵抗奖励骇客 (Reward Hacking)：二元奖励非常严格，只有完全正确的回答才能获得奖励。这避免了模型通过生成一些花哨、冗长但部分错误的回答来“欺骗”连续奖励函数以获得部分分数。
信号清晰且统一：该奖励信号简洁明了，没有噪声，并且能统一应用于长篇生成和短问答两种不同类型的任务。
自然鼓励合理拒答：在强化学习框架下，错误的回答会得到0奖励，其生成概率被压制。这间接提升了模型在不确定时选择“我不知道”等拒答行为的概率，而这种行为是从基座模型继承而来的。

实验结论

本文在Qwen3-4B和Qwen3-8B模型上进行了广泛实验，覆盖了4个幻觉评测基准和10个通用能力评测基准。

主要实验结果

幻觉显著减少：Binary RAR 在所有方法中取得了最好的幻觉减少效果。在长篇生成任务中，Qwen3-8B模型的幻觉率从76.2%降低到45.8%，实现了39.3%的相对降幅，远超SFT、DPO和使用连续奖励的RL基线。在短问答任务中，不正确答案的比例也从60.6%降至27.6%。
通用能力得到保持：最关键的是，事实性的提升并未以牺牲通用能力为代价。如下表所示，经过Binary RAR训练后，模型在指令遵循（如AlpacaEval 2.0）、数学和代码等10个通用能力基准上的表现与原始模型基本持平。相比之下，使用连续奖励（VeriScore）的RL方法虽然也提升了事实性，但在通用能力上却出现了明显衰退（例如，AlpacaEval 2.0得分下降了22.8%）。
学会了校准的拒答 (Calibrated Abstention)：在短问答任务中，经过训练的模型学会了在知识不足时回答“我不知道”，从而大幅减少了错误回答的数量，同时基本保持了在有能力回答问题上的准确率。这表明模型提升了不确定性校准能力，而不是遗忘了知识。

下方表格总结了不同方法在减少幻觉方面的表现：


方法	长篇生成 (FactScore Prec.) ↑	短问答 (Hallucination Rate) ↓
Qwen3-8B Base	38.1	60.6
SFT	37.1 (-1.0)	60.2 (-0.4)
DPO	46.6 (+8.5)	57.2 (-3.4)
RL (LM Judge)	34.6 (-3.5)	56.4 (-4.2)
RL (VeriScore, continuous)	59.4 (+21.3)	42.3 (-18.3)
RL (Binary RAR, 本文方法)	62.5 (+24.4)	27.6 (-33.0)

下方表格展示了不同方法在保持通用能力方面的表现（以相对基座模型的变化量着色）：


方法	AlpacaEval	IF-Eval	MT-Bench	TruthfulQA	PopQA	BBH	GSM8K	MATH	HumanEval	MBPP	平均
Qwen3-8B Base	54.7	18.7	8.86	20.2	48.2	70.8	83.2	41.5	45.1	63.3	61.6
SFT	51.5	17.0	8.88	19.4	46.1	70.0	83.1	42.1	45.1	60.9	60.5 (-1.8%)
DPO	52.8	17.5	8.90	18.9	47.9	69.8	83.5	41.6	45.7	62.1	60.9 (-1.1%)
RL (LM Judge)	54.3	18.4	8.87	15.6	45.0	69.8	83.1	41.4	45.1	63.4	60.6 (-1.6%)
RL (VeriScore)	42.2	14.9	8.83	20.1	47.7	70.3	82.5	41.7	45.1	62.4	59.6 (-3.2%)
RL (Binary RAR)	55.4	18.2	8.86	20.6	48.8	70.8	82.9	41.5	45.1	63.8	62.2 (+1.0%)

核心结论分析

分析表明，Binary RAR 的成功源于其能让模型在保持信息量的同时，选择性地剔除不正确的内容。如下图所示，在长篇生成中，虽然总声明数量减少，但正确声明的数量几乎不变，这表明模型是在提高回答的“精度”而非“减少细节”。

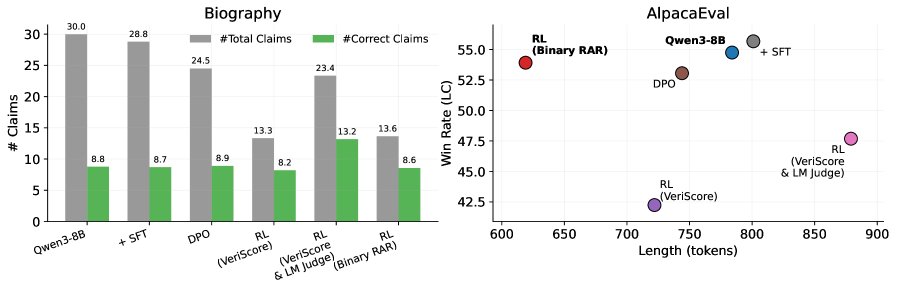长篇生成中的信息量分析左图：在WildChat上，Binary RAR减少了总声明数，但正确声明数几乎不变，表明其在选择性地过滤不确定内容。右图：在AlpacaEval 2.0上，Binary RAR生成的回答更短，但胜率相似，表明其在保持简洁的同时未损失质量。

最终结论：使用二元、检索验证的奖励信号进行在线强化学习（即Binary RAR），是一种稳定且有效的方法，它能够在不牺牲模型通用能力的情况下，显著增强模型的真实可靠性，为解决幻觉-效用权衡问题提供了一个有力的方案。