Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality

• ArXiv URL: http://arxiv.org/abs/2405.21060v1

• 作者: Tri Dao; Albert Gu

• 发布机构: Carnegie Mellon University; Princeton University

---

TL;DR

本文通过揭示结构化状态空间模型 (SSM) 与注意力机制在结构化半可分矩阵 (semiseparable matrices) 理论下的对偶关系，提出了一个名为“状态空间对偶 (State Space Duality, SSD)”的统一框架，并基于此设计了一种新的、更高效的语言模型架构 Mamba-2。

关键定义

• 状态空间对偶 (State Space Duality, SSD)：本文提出的一个理论框架，它通过结构化矩阵的抽象，建立了结构化状态空间模型 (SSM) 与多种注意力变体之间的联系。该框架揭示了模型可以同时拥有类似 SSM 的线性时间复杂度的“循环形式”和类似注意力的二次时间复杂度的“对偶形式”。
• 半可分矩阵 (Semiseparable Matrix)：一种特殊的结构化矩阵。其核心特征是，任何完全位于其主对角线下方（或之上）的子矩阵，其秩 (rank) 不会超过一个常数 N（称为半可分阶）。本文证明了 SSM 的序列转换等价于与一个半可分矩阵的乘法。
• 序列半可分表示 (Sequentially Semiseparable Representation, SSS)：半可分矩阵的一种具体生成式表示。一个下三角矩阵 $M$ 若能表示为 $M_{ji} = C_j^{\top} A_j \cdots A_{i+1} B_i$ 的形式，则称其拥有 SSS 表示。本文证明 SSM 的矩阵形式天然就是 SSS 表示。
• 结构化掩码注意力 (Structured Masked Attention, SMA)：本文对线性注意力 (Linear Attention) 的一种推广。其核心思想是，在计算注意力时所用的掩码矩阵 $L$ 不再局限于传统的因果掩码（全1下三角阵），而是可以是任何拥有快速矩阵向量乘法算法的结构化矩阵。

相关工作

当前，以 Transformer 为主的解码器模型（如 GPT、Llama）是深度学习在语言建模领域取得成功的核心驱动力。然而，其核心的注意力层在训练时存在序列长度的二次方复杂度伸缩问题，在自回归生成时也需要线性大小的缓存，这限制了其处理长序列的效率。

与此同时，另一类序列模型——结构化状态空间模型 (Structured State Space Models, SSMs)，如 S4 和 Mamba，展现出线性时间复杂度的训练能力和恒定大小的生成状态，并在中等规模上表现出与 Transformer 相当甚至更好的性能。

本文旨在解决的问题是：SSM 的发展似乎与主流的 Transformer 改进工作脱节，导致其理论理解、社区生态和系统优化相对滞后。本文的目标是建立 SSM 和注意力之间的深层理论联系，从而将为 Transformer 开发的成熟算法和系统优化技术迁移到 SSM 上，构建出性能优于 Transformer 且对序列长度伸缩性更好的基础模型。

本文方法

状态空间对偶 (SSD) 框架

本文的核心贡献是提出了状态空间对偶 (State Space Duality, SSD) 框架，它通过结构化矩阵这一桥梁，统一了状态空间模型 (SSM) 和注意力 (Attention) 这两大看似不同的序列模型家族。

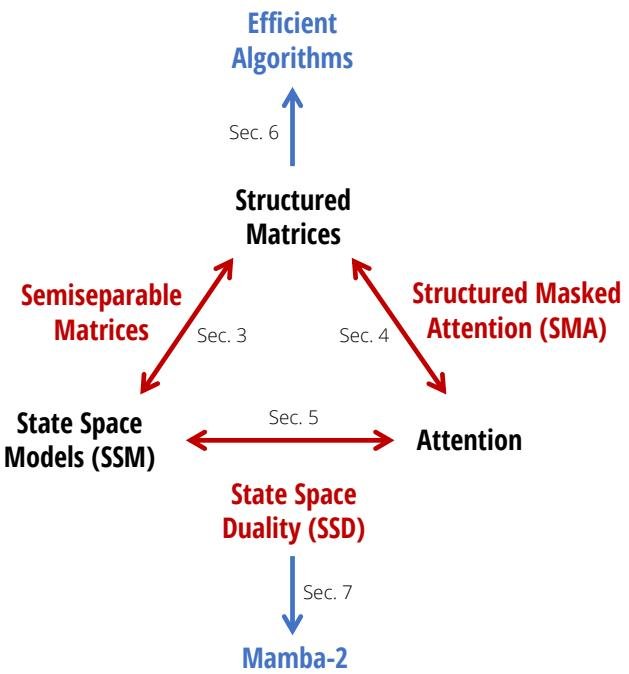
该框架揭示了模型可以从两种对偶的视角进行计算：

1. 循环（线性）形式 (Recurrent Form)：模型表现为一种状态空间递归，计算复杂度与序列长度 $T$呈线性关系 $O(T)$。这种形式高效，适合长序列处理和自回归生成。
2. 对偶（二次）形式 (Dual Form)：模型表现为一种类似注意力的矩阵乘法，计算复杂度与序列长度 $T$ 呈二次关系 $O(T^2)$。这种形式与注意力机制相似，能够利用现代硬件（如 GPU）上高度优化的矩阵运算单元。

SSM 即半可分矩阵

本文首先揭示了 SSM 的一个基本数学性质：任何 SSM 所代表的序列到序列的转换，都可以等价地表示为一个矩阵-向量乘法 $y = Mx$。

对于一个由参数 $(A_t, B_t, C_t)$ 定义的选择性 SSM：

\[h_t = A_t h_{t-1} + B_t x_t\] \[y_t = C_t^\top h_t\]

可以推导出其矩阵形式 $y=Mx$ 中，矩阵 $M$ 的元素为：

\[M_{ji} := C_j^\top A_j \cdots A_{i+1} B_i \quad (\text{for } j \ge i)\]

这种形式正是 序列半可分 (Sequentially Semiseparable, SSS) 矩阵的定义。而 SSS 矩阵是更广泛的 半可分矩阵 (Semiseparable Matrix) 的一种表示。半可分矩阵是一种结构化矩阵，其位于主对角线下方的任何子矩阵的秩都受限于一个常数N（即SSM的状态维度）。

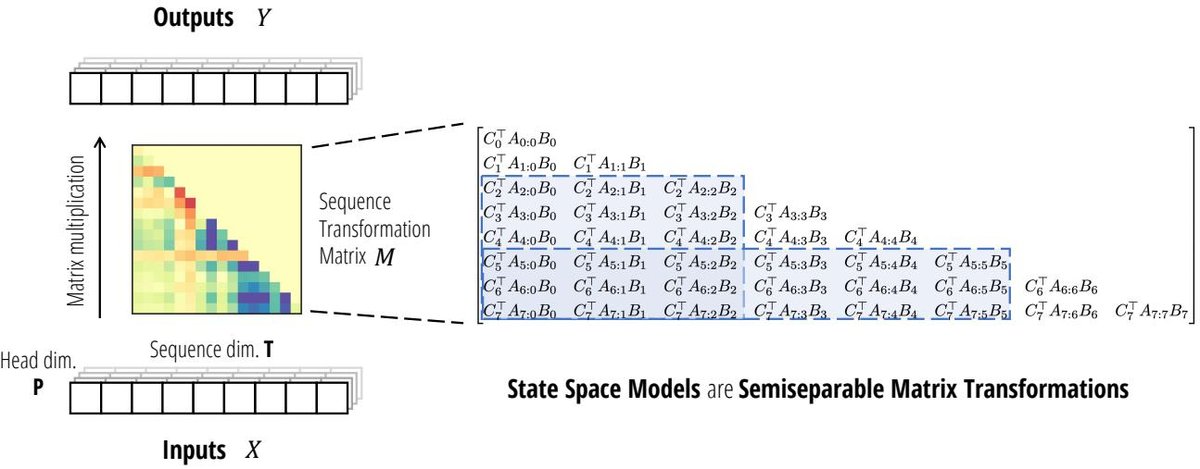
这个发现（定理3.5）是本文理论的基石。它意味着：

• 计算 SSM 的前向传播等价于执行一次半可分矩阵的矩阵-向量乘法。
• 所有针对半可分矩阵的高效算法都可以被用来加速 SSM 的计算。
• 这为理解 SSM 的计算特性提供了全新的“矩阵视角”，超越了传统的“循环”或“卷积”视角。

结构化掩码注意力 (SMA)

接着，本文从注意力机制出发，提出了对线性注意力 (Linear Attention) 的推广，即 结构化掩码注意力 (Structured Masked Attention, SMA)。

传统的掩码核注意力 (Masked Kernel Attention) 计算可以写成：

\[y = (L \circ (QK^{\top})) \cdot V\]

其中 $L$ 是掩码矩阵，对于因果注意力，$L$ 是一个下三角全1矩阵。

线性注意力的关键技巧是通过改变运算顺序来获得线性复杂度，但这严重依赖于 $L$ 是因果掩码的特性，因为与 $L$ 相乘等价于一次累加 (cumsum) 操作，这是一种线性时间复杂度的递归。

本文通过张量收缩 (tensor contraction) 的视角重新审视了这一过程，并指出，只要掩码矩阵 $L$ 是一个拥有快速（亚二次方复杂度）矩阵-向量乘法算法的结构化矩阵，就可以实现高效计算。

定义4.2 (SMA)：结构化掩码注意力被定义为一个四元张量收缩：

\[Y = \text{contract(TN, SN, SP, TS} \rightarrow \text{TP)}(Q, K, V, L)\]

其中 $Q, K, V$ 是标准注意力输入，$L$ 是任意一个结构化矩阵。

这个定义统一了多种注意力变体：

• 线性注意力: $L$ 是因果掩码（下三角1矩阵）。
• RetNet: $L$ 是一个带有指数衰减的下三角矩阵。

SSD 算法与 Mamba-2 架构

创新点

结合以上两个发现，本文设计了新的 SSD 算法和 Mamba-2 架构。

SSD 算法： SSD 算法是一种新的 SSM 计算方法，它基于半可分矩阵的块分解 (block decomposition)。该算法巧妙地结合了线性递归和二次矩阵乘法的优点，实现了在计算、内存和硬件利用率等多个维度上的最佳权衡。相比 Mamba 中优化的选择性扫描 (selective scan) 算法，SSD 算法的专用实现速度提升了 2-8 倍，并且允许使用更大的循环状态（比 Mamba 大8倍以上），而速度下降很小。

Mamba-2 架构： Mamba-2 是一个基于 SSD 框架设计的新架构。它对原始的 Mamba 模块进行了几处关键修改，使其更加高效且易于并行化：

1. 采用 SSD 层：用更快的 SSD 算法替代了 Mamba 的核心选择性扫描层。
2. 引入多头结构：类似于多头注意力 (Multi-Head Attention, MHA)，Mamba-2 引入了头的概念，并发现 Mamba 架构本身可以被看作是多值注意力 (Multi-Value Attention, MVA) 的一种模拟。
3. 支持张量并行 (Tensor Parallelism)：通过调整模块结构，如引入分组值注意力 (Grouped-Value Attention, GVA) 头结构，并将所有数据依赖的投影操作移至模块开头并行执行，使得 Mamba-2 能像 Transformer 一样方便地进行张量并行训练。

这些改进使得 Mamba-2 不仅在算法层面更快，也在系统层面更易于扩展到大规模训练，解决了之前 SSM 模型难以高效并行化的问题。

算法步骤	张量收缩表示	输出形状
输入扩展	\(Z = contract(SP,SPN)(X, B)\)	(S, P, N)
独立标量SSM	\(H = contract(TSN,TPN)(L, Z)\)	(T, P, N)
状态收缩	\(Y = contract(TN, TPN -> TP)(C, H)\)	(T, P)

上表为对角结构化SSM线性模式计算的张量收缩形式，SSD算法通过块分解对此过程进行了优化。

实验结论

本文通过一系列实验验证了 Mamba-2 的有效性：

• 训练效率：在语言建模任务上，SSD 算法的实现比 Mamba 的选择性扫描快 2-8 倍。与 FlashAttention-2 相比，SSD 在序列长度超过 2K 时开始显现优势，在 16K 长度时速度快 6 倍。
• 模型性能 (Chinchilla Scaling Laws)：在同等计算预算下，Mamba-2 的困惑度 (perplexity) 和训练墙钟时间 (wall-clock time) 均优于 Mamba 和 Transformer++，实现了帕累托最优。
• 下游任务评估：在 Pile 数据集上，一个 2.7B 参数的 Mamba-2 模型（在 300B tokens 上训练）在标准下游评估中，其性能超过了同样在此数据集上训练的 Mamba-2.8B、Pythia-2.8B 甚至 Pythia-6.9B 模型。
• 长序列任务：在多查询关联召回任务 (multi-query associative recall) 上，Mamba-2 也表现出色，验证了其处理长距离依赖的能力。

最终结论：本文通过建立 SSM 和注意力之间的对偶关系，不仅提供了对这些模型更深层次的理论理解，还催生了具体的算法 (SSD) 和架构 (Mamba-2) 创新。实验证明，Mamba-2 作为一个新的基础模型架构，在保持与 Transformer 相当甚至更好性能的同时，显著提升了训练和推理效率，尤其在处理长序列方面具有巨大潜力。