Transition Models: Rethinking the Generative Learning Objective
-
ArXiv URL: http://arxiv.org/abs/2509.04394v1
-
作者: Yiyuan Zhang; Xiaoyu Yue; Wanli Ouyang; Yangguang Li; Xiangyu Yue; Zidong Wang; Lei Bai
-
发布机构: Shanghai AI Lab; The Chinese University of Hong Kong; University of Sydney
TL;DR
本文提出了一种名为过渡模型 (Transition Models, TiM) 的新型生成范式，它通过学习一个能够在任意时间间隔 \($\Delta t\)$ 上进行状态转换的精确动力学方程，成功统一了高效的少步生成与高质量的多步精炼，解决了现有生成模型中普遍存在的“速度-质量”权衡困境。
关键定义
本文的核心是围绕一个新的生成学习目标展开的，其关键概念如下：
-
过渡模型 (Transition Models, TiM): 一种新型的生成模型，其训练目标并非像传统扩散模型那样学习瞬时的 PF-ODE 向量场，也不是像一致性模型那样学习固定的终点映射，而是直接学习在任意时间点 \(t\) 的状态 \($\mathbf{x}\_t\)$ 到任意先前时间点 \($t-\Delta t\)$ 的状态 \($\mathbf{x}\_{t-\Delta t}\)$ 之间的转换。这使得单个模型就能适应从单步跳跃到多步精细化采样的任意步长策略。
-
状态转换恒等式 (State Transition Identity): 本文推导出的一个核心数学关系，即 \($\frac{\mathrm{d}}{\mathrm{d}t}(B\_{t,r}\cdot(\hat{\alpha}\_{t}\mathbf{x}+\hat{\sigma}\_{t}\mathbf{\varepsilon}-\mathbf{f}\_{\theta,t,r}))=0\)$。该恒等式对模型施加了双重约束：1) 隐式轨迹一致性，确保从 \(t\) 到 \(r\) 的直接转换等价于任何中间步骤的组合，保证了采样路径的稳定性；2) 时间斜率匹配，迫使模型不仅要最小化当前残差，还要最小化残差随时间的变化率，从而学习到更平滑的解流形。
-
微分推导方程 (Differential Derivation Equation, DDE): 一种用于高效计算网络时间导数 \($\frac{\mathrm{d}\mathbf{f}\_{\theta}}{\mathrm{d}t}\)$ 的有限差分近似方法。与计算密集且与分布式训练框架（如 FSDP）不兼容的雅可比向量积 (Jacobian-Vector Product, JVP) 不同，DDE 仅需前向传播，速度快约2倍且具有良好的可扩展性，使得对十亿级参数的大模型进行从头训练成为可能。
相关工作
当前视觉内容生成领域由扩散模型主导，但面临一个根本性的困境：
- 多步模型（如扩散模型）：通过对概率流常微分方程 (Probability-Flow Ordinary Differential Equation, PF-ODE) 进行迭代数值积分来生成高质量图像。这种方法保真度高，但需要大量的函数评估次数 (Number of Function Evaluations, NFE)，导致推理延迟大、计算成本高。当采样步长 \($\Delta t\)$ 增大时，离散化误差会急剧增加，导致性能下降。
- 少步模型（如一致性模型、FlowMap）：通过学习从噪声到数据的直接映射或轨迹上的“捷径”来减少采样步数。这类模型在少步生成上效率很高，但存在一个难以逾越的“质量天花板”。由于它们在训练中丢弃了精细的局部动态信息，增加采样步数通常不会带来性能提升，甚至可能导致质量下降。
本文旨在解决上述两难困境，即模型要么保真度高但计算昂贵，要么效率高但牺牲了精炼能力。本文提出的问题是：什么才是生成模型最合适的学习目标？ 作者认为，一个理想的目标应该能让模型学习一个通用的、由时间间隔 \($\Delta t\)$ 参数化的去噪算子，从而在少步和多步生成场景下都能表现出色，并随着计算预算的增加而单调提升质量。
图 2: 不同生成范式图示。传统扩散模型学习局部向量场，少步模型学习固定的终点映射（单个大步），而本文的过渡模型 (TiM) 训练用于掌握任意状态间的转换。这种方法使 TiM 能够学习生成过程的整个解流形，统一了少步和多步生成机制。
本文方法
本文首先分析了传统PF-ODE监督的局限性，然后推导出一个适用于任意时间间隔的状态转换恒等式，并基于此构建了一个可扩展且稳定的学习目标。最后，提出了针对性的架构改进。
PF-ODE监督的局限性
扩散模型通过前向过程 \($ \mathbf{x}\_{t}=\alpha\_{t}\mathbf{x}+\sigma\_{t}\mathbf{\varepsilon}\)$ 对数据进行加噪。其生成过程等价于求解一个逆时 PF-ODE：
\[\frac{\mathrm{d}\mathbf{x}_{t}}{\mathrm{d}t} = \mathrm{f}(\mathbf{x}_{t},t)-\frac{1}{2}\mathrm{g}(t)^{2}\nabla_{\mathbf{x}_{t}}\log p_{t}(\mathbf{x}_{t})\]模型的训练目标 \($\mathbf{f}\_{\theta}(\mathbf{x}\_{t},t)\)$ 实质上是在监督这个微分方程的向量场。在采样时，需要使用数值求解器进行积分。为了保证精度，步长 \($\Delta t\)$ 必须很小，这导致了高昂的 NFE。
状态转换
本文方法的核心是从第一性原理出发，将状态转换视为一个必须对任意时间间隔 \($\Delta t = t - r\)$ 精确成立的恒等式，而非数值近似。
状态转换恒等式
从任意状态 \($\mathbf{x}\_t\)$ 可以预测出 \($\hat{x}\)$ 和 \($\hat{\mathbf{\varepsilon}}\)$，进而可以表示任意先前的状态 \($\mathbf{x}\_r = \alpha\_r \hat{\mathbf{x}} + \sigma\_r \hat{\mathbf{\varepsilon}}\)$。将此过程用一个依赖于起始时间 \(t\) 和目标时间 \(r\) 的网络 \($\mathbf{f}\_{\theta}(\mathbf{x}\_{t},t,r)\)$ 来参数化，可以得到：
\[\mathbf{x}_{r}=\frac{(\alpha_{r}\hat{\sigma}_{t}-\sigma_{r}\hat{\alpha}_{t})\mathbf{x}_{t}+(\sigma_{r}\alpha_{t}-\alpha_{r}\sigma_{t})\mathbf{f}_{\theta}(\mathbf{x}_{t},t,r)}{\hat{\sigma}_{t}\alpha_{t}-\hat{\alpha}_{t}\sigma_{t}}\]将上式简写为 \($\mathbf{x}\_r = A\_{t,r}\mathbf{x}\_t + B\_{t,r}\mathbf{f}\_{\theta,t,r}\)$。通过对时间 \(t\) 求导并整理，本文推导出一个关键的状态转换恒等式：
\[\frac{\mathrm{d}(B_{t,r}\cdot(\hat{\alpha}_{t}\mathbf{x}+\hat{\sigma}_{t}\mathbf{\varepsilon}-\mathbf{f}_{\theta,t,r}))}{\mathrm{d}t}=0\]该恒等式展开后包含两项：
\[(\underbrace{\hat{\alpha}_{t}\mathbf{x}+\hat{\sigma}_{t}\mathbf{\varepsilon}-\mathbf{f}_{\theta,t,r}}_{\text{PF-ODE supervision}})\frac{\mathrm{d}B_{t,r}}{\mathrm{d}t}+B_{t,r}\underbrace{\frac{\mathrm{d}(\hat{\alpha}_{t}\mathbf{x}+\hat{\sigma}_{t}\mathbf{\varepsilon}-\mathbf{f}_{\theta,t,r})}{\mathrm{d}t}}_{\text{time-slope matching}}=0\]这个恒等式强加了比传统扩散模型更严格的约束：
- 隐式轨迹一致性：它要求加权残差 \($B\_{t,r}h(t)\)$（其中 \($h(t)\)$ 是瞬时残差）对于任何以 \($\mathbf{x}\_r\)$ 为终点的轨迹，其值在整个轨迹上保持不变。这确保了多步采样路径的内在一致性，使得增加采样步骤成为一种精炼而非偏离。
- 时间斜率匹配：它不仅要求瞬时残差 \($h(t) \to 0\)$（传统目标），还要求残差的时间导数 \($\frac{\mathrm{d}}{\mathrm{d}t}h(t) \to 0\)$。这种高阶监督使得模型学习到的解流形更平滑，在大步长采样时保持连贯性，在小步长时保证稳定精炼。
学习目标
基于状态转换恒等式，本文导出了一个动态的学习目标 \($\hat{\mathbf{f}}\)$：
\[\hat{\mathbf{f}}=\hat{\alpha}_{t}\mathbf{x}+\hat{\sigma}_{t}\mathbf{\varepsilon}+\frac{B_{t,r}}{\frac{\mathrm{d}B_{t,r}}{\mathrm{d}t}}\left(\frac{\mathrm{d}\hat{\alpha}_{t}}{\mathrm{d}t}\mathbf{x}+\frac{\mathrm{d}\hat{\sigma}_{t}}{\mathrm{d}t}\mathbf{\varepsilon}-\frac{\mathrm{d}\mathbf{f}_{\theta^{-},t,r}}{\mathrm{d}t}\right)\]其中 \($\theta^{-}\)$ 表示固定的网络参数。最终的 TiM 训练目标为：
\[\mathbb{E}_{\mathbf{x},\mathbf{\varepsilon},t,r}\left[w(t,r)\cdot d\left(\mathbf{f}_{\theta}(\mathbf{x}_{t},t,r)-\hat{\mathbf{f}}\right)\right]\]其中 \($w(t,r)\)$ 是一个为稳定训练而引入的权重函数。
训练的可扩展性与稳定性
-
可扩展性 (Scalability): 为解决学习目标中计算时间导数 \($\frac{\mathrm{d}\mathbf{f}\_{\theta^{-},t,r}}{\mathrm{d}t}\)$ 带来的可扩展性瓶颈（传统JVP方法无法与现代训练优化兼容），本文提出了微分推导方程 (DDE) 进行近似：
\[\frac{\mathrm{d}\mathbf{f}_{\theta^{-},t,r}}{\mathrm{d}t}\approx\frac{\mathbf{f}_{\theta^{-}}(\mathbf{x}_{t+\epsilon},t+\epsilon,r)-\mathbf{f}_{\theta^{-}}(\mathbf{x}_{t-\epsilon},t-\epsilon,r)}{2\epsilon}\]DDE 仅需前向传播，计算效率高，且与 FlashAttention 和 FSDP 等分布式训练技术兼容，使得训练大模型成为可能。
| 方法 | 算子 | 训练 | FID | ||||
|---|---|---|---|---|---|---|---|
| FLOPs (G) | 延迟 (ms) | 吞吐量 (/s) | 显存 (GiB) | NFE=1 | NFE=8 | NFE=50 | |
| JVP | 48.29 | 213.14 | 1.80 | 14.89 | 49.75 | 26.22 | 18.11 |
| DDE | 24.14 | 110.08 | 2.40 | 15.23 | 49.91 | 26.09 | 17.99 |
-
稳定性 (Stability): 在训练中，过大的时间间隔 \($\Delta t\)$ 可能导致梯度方差过大和训练不稳定。为此，本文设计了一个损失权重函数 \($w(t,r)\)$，它优先考虑较短的时间间隔，为训练提供更稳定的信号。最终采用的权重函数为：
\[w(t,r)=({\sigma_{\text{data}}+\tan(t)-\tan(r)})^{-\frac{1}{2}}\]
架构改进
为使模型能有效学习状态转换，本文对 DiT 架构进行了两点改进：
-
解耦的时间与间隔嵌入 (Decoupled Time and Interval Embeddings): 使用两个独立的时间编码器 \($\phi\_t\)$ 和 \($\phi\_{\Delta t}\)$ 分别编码绝对时间 \(t\) 和过渡间隔 \($\Delta t\)$，然后将它们的输出相加 \($\mathbf{E}\_{t,\Delta t}=\phi\_{t}(t)+\phi\_{\Delta t}(\Delta t)\)$。这使得模型能明确区分当前所处的时间点和需要跨越的时间长度。
-
间隔感知注意力 (Interval-Aware Attention): 假设空间依赖性的建模方式应取决于过渡间隔 \($\Delta t\)$ 的大小（大步长关注全局，小步长关注局部）。因此，将间隔嵌入 \($\mathbf{E}\_{\Delta t}\)$ 直接注入到注意力机制的查询 (query)、键 (key) 和值 (value) 的计算中：
\[\begin{aligned} \mathbf{q} &= \mathbf{z}\mathbf{W}_{q}+\mathbf{b}_{q}+\mathbf{E}_{\Delta t}\mathbf{W}^{\prime}_{q}, \\ \mathbf{k} &= \mathbf{z}\mathbf{W}_{k}+\mathbf{b}_{k}+\mathbf{E}_{\Delta t}\mathbf{W}^{\prime}_{k}, \\ \mathbf{v} &= \mathbf{z}\mathbf{W}_{v}+\mathbf{b}_{v}+\mathbf{E}_{\Delta t}\mathbf{W}^{\prime}_{v}. \end{aligned}\]这使得自注意力机制可以根据间隔大小动态调整其行为。
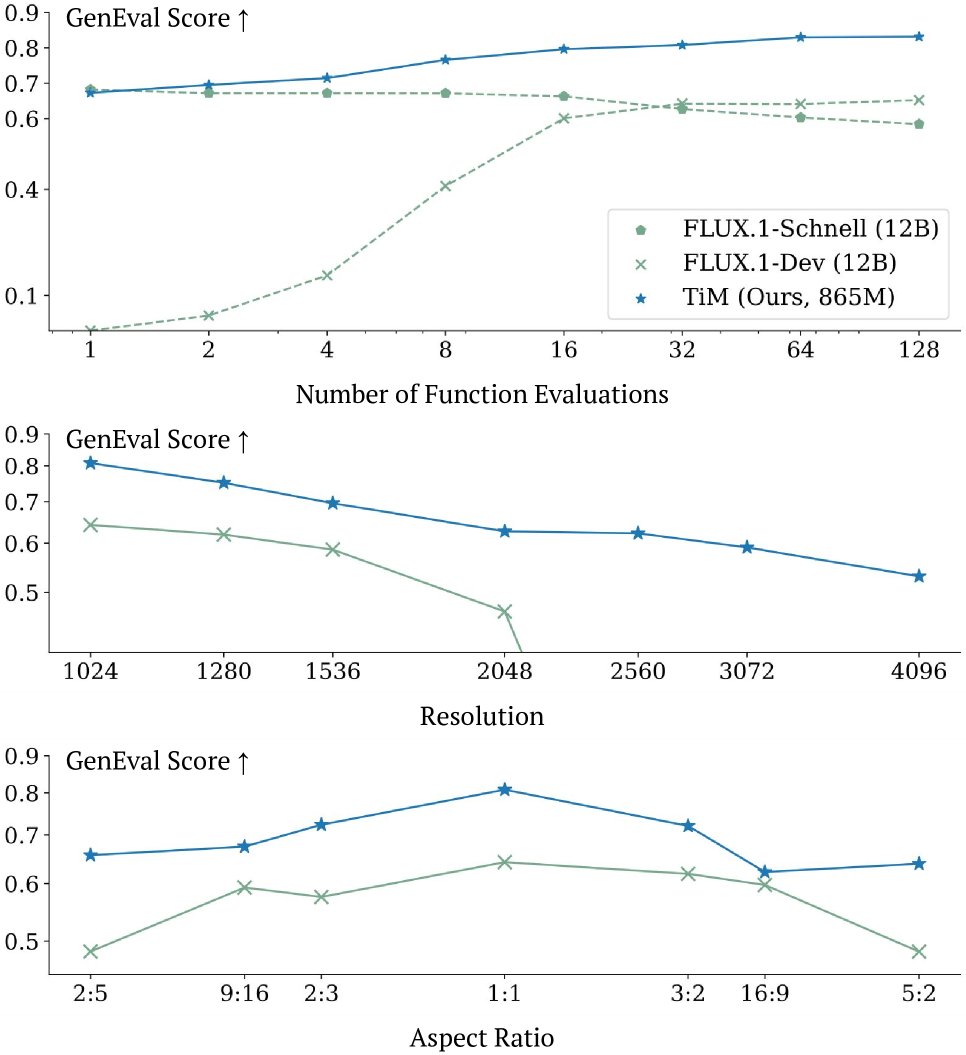图 1: TiM 在不同 NFE、分辨率和宽高比下的卓越性能。
实验结论
关键实验结果
TiM 在各类文生图基准测试中展现了最先进的性能、效率和灵活性。
- 性能与效率：在 GenEval 基准上，仅有 865M 参数的 TiM 在单步采样 (1-NFE) 时得分（0.67）就超过了许多大型蒸馏模型，并在增加到 128-NFE 时得分（0.83）超越了数十亿参数的 SD3.5-Large (8B) 和 FLUX.1-Dev (12B) 等业界领先模型。
- 单调质量提升：如 Table 5 所示，TiM 是唯一一个随着 NFE 增加，生成质量单调提升的模型。相比之下，FLUX.1-Schnell 等蒸馏模型在 NFE 增加时性能下降，而 SD3.5-Large 等标准扩散模型在低 NFE 时直接失效。这一特性证明 TiM 成功解决了“速度-质量”的权衡。
- 跨分辨率与宽高比泛化：如 Table 6 所示，得益于原生分辨率训练策略，TiM 在高达 \(4096x4096\) 的分辨率和各种非常规宽高比上表现出强大的泛化能力，显著优于竞争对手。
- T2I 基准测试：在 MJHQ30K 和 DPGBench 等基准上 (Table 3)，TiM 以更少的 NFE 取得了比 SDXL 等模型更优的 FID 和 CLIP 分数，证明了其卓越的图像质量和文本对齐能力。
图 3: 不同 NFE 下的定性比较。TiM 在所有 NFE 下均提供出色的保真度和文本对齐。
| 方法 | NFE=1 | NFE=8 | NFE=32 | NFE=128 |
|---|---|---|---|---|
| SD3.5-Turbo [61] | 0.50 | 0.66 | 0.70 | 0.70 |
| FLUX.1-Schnell [6] | 0.68 | 0.67 | 0.63 | 0.58 |
| SD3.5-Large [20] | 0.00 | 0.50 | 0.69 | 0.70 |
| FLUX.1-Dev [5] | 0.00 | 0.40 | 0.64 | 0.65 |
| TiM | 0.67 | 0.76 | 0.80 | 0.83 |
表 5: 在 GenEval 基准上跨 NFE 的生成质量对比 (得分↑)。TiM展现了随 NFE 增加而单调提升的质量。
消融研究
在 ImageNet-256 数据集上的消融实验验证了各项设计的有效性 (Table 4)。
- 训练目标：将基线模型的标准扩散目标替换为 TiM 目标后，1-NFE 的 FID 从 309.5 大幅降低到 49.91，证明了学习任意转换对少步生成的关键作用。同时，DDE 方法在不损失性能的情况下实现了可扩展性。
- 架构贡献：解耦时间嵌入和间隔感知注意力机制均能独立提升性能，而将两者结合使用时效果最佳，证明了让模型显式理解时间和间隔的互补性和必要性。
- 训练策略：在最佳架构基础上加入间隔权重策略，能进一步稳定地提升所有 NFE 设置下的性能。
| 方法 | NFE=1 | NFE=8 | NFE=50 |
|---|---|---|---|
| 训练目标 | |||
| (a) 基线 (SiT-B/4) | 309.5 | 77.26 | 20.35 |
| (b) TiM-B/4 (使用 JVP) | 49.75 | 26.22 | 18.11 |
| (c) TiM-B/4 (使用 DDE) | 49.91 | 26.09 | 17.99 |
| 架构 | |||
| (d) 原始架构 | 56.22 | 28.75 | 20.37 |
| (e) + 解耦时间嵌入 (De-TE) | 49.91 | 26.09 | 17.99 |
| (f) + 间隔感知注意力 (IA-Attn) | 48.38 | 26.10 | 17.85 |
| (g) + De-TE + IA-Attn | 48.30 | 25.05 | 17.43 |
| 训练策略 (在(g)基础上) | |||
| (h) + 时间权重 | 47.46 | 24.62 | 17.10 |
表 4: 在 ImageNet-256 上的消融研究 (FID↓)。
最终结论
本文提出的过渡模型 (TiM) 是一种更高效、更强大的生成范式。通过一个统一的模型，它不仅解决了生成领域长期存在的速度-质量权衡问题，实现了从单步到多步的质量单调提升，还在一个紧凑的模型（865M）中超越了数倍于其大小的业界模型，并展现了出色的高分辨率生成能力。这项工作为下一代兼具高效、可扩展和创造潜力的基础模型铺平了道路。