Tree of Thoughts: Deliberate Problem Solving with Large Language Models
-
ArXiv URL: http://arxiv.org/abs/2305.10601v2
-
作者: Jeffrey Zhao; Karthik Narasimhan; Izhak Shafran; Dian Yu; Yuan Cao; Shunyu Yao; T. Griffiths
-
发布机构: Google DeepMind; Princeton University
TL;DR
本文提出了一种名为“思想树”（Tree of Thoughts, ToT）的新型语言模型推理框架，它通过将问题解决过程建模为对“思想”（连貫的文本单元）树的探索，使大型语言模型能够进行深思熟虑的决策、前瞻和回溯，从而显著提升其在需要规划和搜索的复杂任务上的解决能力。
关键定义
本文的核心是“思想树”框架，其中包含以下几个关键概念：
- 思想树 (Tree of Thoughts, ToT)：一个通用问题解决框架，它将问题求解过程视为在一棵树上进行搜索。树的节点代表一个包含部分解的状态，而树枝则代表用于修改状态的操作（即生成新的思想）。
- 思想 (Thought)：一个连贯的语言序列，作为解决问题的中间步骤。与传统的逐个Token生成不同，“思想”是一个有意义的语义单元，例如一个方程式、一段写作计划或一个待填写的单词。
- 思想生成器 (Thought Generator)：给定一个树状态（即部分解），该模块负责生成一组潜在的、用于下一步探索的思想。
- 状态评估器 (State Evaluator)：该模块负责评估不同状态（即不同的“思想”分支）的进展，为搜索算法提供启发式信息，以决定探索哪些状态以及探索的顺序。本文的一个核心创新是让语言模型自身通过深思熟虑的推理来扮演评估器的角色。
相关工作
当前，使用大型语言模型（LMs）解决问题的主要方法，如输入-输出（IO）提示和思想链（Chain-of-Thought, CoT），都依赖于自回归的、从左到右的Token生成机制。这种机制类似于人类认知中的“系统1”思维——快速、自动，但缺乏深思熟虑的规划。
这些方法的关键瓶颈在于：
- 缺乏探索性：在生成过程的每一步，它们通常只选择一个最优或一个采样路径，而不会探索多种可能性。
- 无全局规划或回溯：一旦做出一个决策（生成一段文本），就无法回头修改。这使得它们在需要战略性前瞻、试错或初始决策至关重要的复杂任务中表现不佳。
本文旨在解决上述问题，通过引入一种更接近人类“系统2”思维的 deliberate planning process，允许模型探索、评估和选择不同的推理路径。
本文方法
为了克服现有方法的局限性，本文提出了思想树（Tree of Thoughts, ToT）框架，将问题求解过程形式化为在一棵树上的搜索。
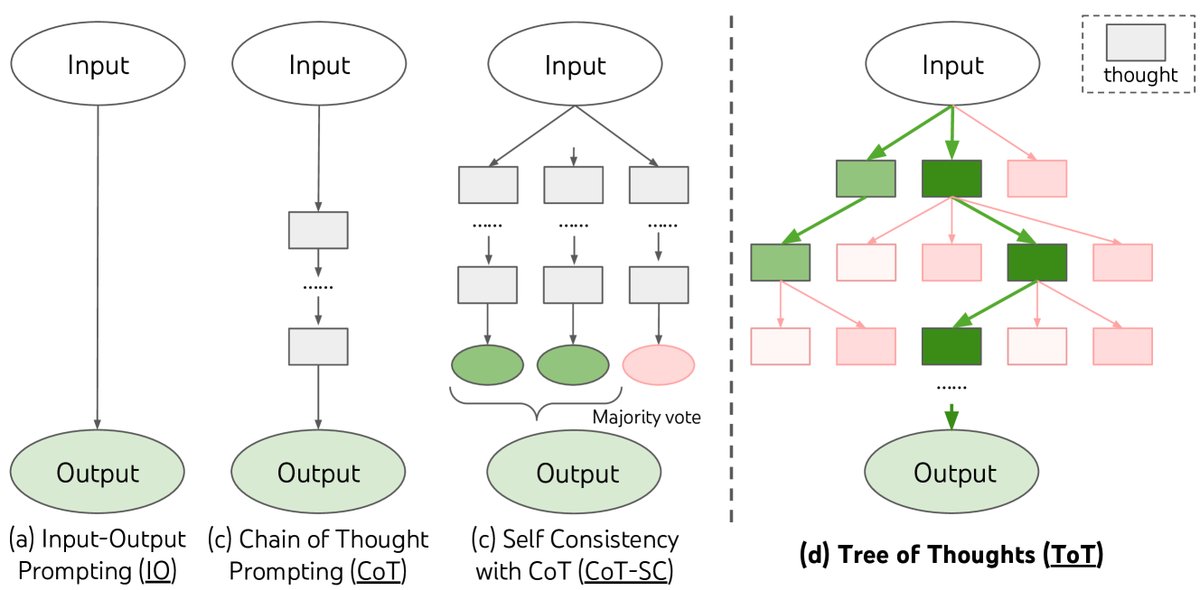
图1：展示了不同的大语言模型问题解决方法。每个矩形框代表一个“思想”，即解决问题的连贯中间步骤。
一个具体的ToT实例需要定义以下四个核心组件：
1. 思想分解 (Thought Decomposition)
ToT的第一步是将问题分解为多个思想步骤。与CoT模糊的连续生成不同，ToT根据问题特性来设计思想单元。一个“思想”的大小应适中：既要小到能让LM生成多样且有前景的候选项，又要大到足以让LM评估其对解决问题的贡献。
| 24点游戏 | 创意写作 | 5x5 填字游戏 | |
|---|---|---|---|
| 输入 | 4个数字 (4 9 10 13) | 4个随机句子 | 10条线索 (h1. presented;..) |
| 输出 | 得到24的等式 (13-9)*(10-4)=24 | 以4个句子结尾的4段连贯文章 | 5x5字母矩阵: SHOWN; WIRRA; AVAIL; … |
| 思想 | 3个中间等式 (13-9=4; 10-4=6; 4*6=24) | 一个简短的写作计划 (1. 引入一本连接…) | 填入线索的单词 (h1. shown; v5. naled; …) |
| ToT步数 | 3 | 1 | 5-10 (可变) |
表1：任务概览，展示了不同任务的思想分解方式。
2. 思想生成器 (Thought Generator)
给定一个状态 $s$，思想生成器 $G(p_{\theta}, s, k)$ 会产生 $k$ 个候选的下一步思想。本文提出了两种策略：
- 独立同分布采样：使用CoT提示独立地采样 $k$ 个思想。这适用于思想空间较大、需要多样性的任务（如创意写作）。
- 序列化提议：使用一个“提议提示”一次性生成多个不同的思想。这适用于思想空间相对受限、需要避免重复的任务（如24点游戏）。
3. 状态评估器 (State Evaluator)
状态评估器 $V(p_{\theta}, S)$ 是ToT的启发式向导。本文的创新之处在于，它利用LM自身来进行深思熟虑的推理评估，而不是依赖于预编程规则或学习模型。
- 独立评估（Value）：对每个状态 $s$ 进行独立打分（例如，1-10分）或分类（例如，“肯定/可能/不可能”）。这种评估可以基于前瞻模拟（如检查数字是否可能凑成24）或常识判断（如某些数字组合太大或太小）。
- 跨状态投票（Vote）：当难以直接为状态打分时（如评估段落连贯性），可以让LM比较多个候选状态，并投票选出最有前途的一个。
4. 搜索算法 (Search Algorithm)
ToT框架是模块化的，可以集成不同的搜索算法。本文实现了两种经典算法：
-
广度优先搜索 (Breadth-First Search, BFS)：在每一步保留 $b$ 个最优质的候选状态，并并行探索。适用于树深度较浅的任务（如24点游戏）。
``\(latex Algorithm 1: ToT-BFS(x, p_theta, G, k, V, T, b)\)`$$
-
深度优先搜索 (Depth-First Search, DFS)：优先探索最有希望的路径，直到达到最终解或评估器认为当前路径不可行（剪枝）。当路径被剪枝时，算法会回溯到父节点探索其他分支。适用于需要更深探索的任务（如填字游戏）。
\(`\)latex Algorithm 2: ToT-DFS(s, t, p_theta, G, k, V, T, v_th) $$``
创新点
ToT方法的核心创新与优点在于：
- 通用性与模块化：它将问题解决抽象为一个通用的“搜索”过程，IO、CoT等方法都可以视为ToT的特例（如树的深度和广度受限）。其模块化设计允许独立更换LM、生成器、评估器和搜索算法。
- 显式探索与规划：与CoT的单一线性路径不同，ToT能主动探索和维护多个推理路径，具备了规划、前瞻和回溯的能力。
- LM驱动的启发式搜索：最关键的创新是利用LM自身进行有意识的、基于推理的自我评估，从而为搜索过程提供灵活且高效的启发式指导，而无需额外训练或硬编码规则。
实验结论
本文在三个专门设计用以挑战现有方法的任务上验证了ToT的有效性，这些任务都需要规划、搜索或创造性思维。
1. 24点游戏 (Game of 24)
这是一个数学推理任务，需要用4个数字和四则运算得到24。
- 结果：ToT取得了压倒性的成功。在使用BFS（广度 $b=5$）时，ToT的成功率达到 74%，而标准的CoT提示仅为 4.0%，CoT-SC（100个样本）也只有9.0%。
- 分析：错误分析表明，超过60%的CoT样本在第一步计算后就已经走上了错误的路径。这凸显了线性、不可回溯方法的脆弱性。ToT通过在每一步探索多个选项并进行评估，有效避免了早期错误。
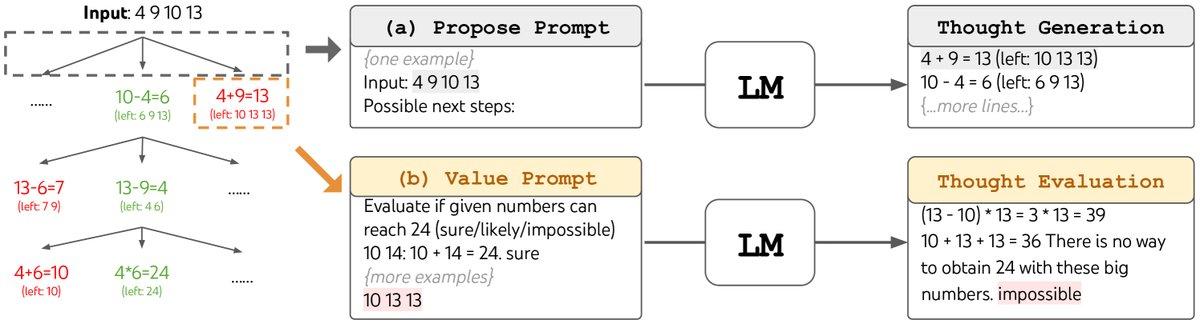图2：在24点游戏中，LM被提示 (a) 生成思想（中间步骤）和 (b) 对其进行评估。
| 方法 | 成功率 |
|---|---|
| IO prompt | 7.3% |
| CoT prompt | 4.0% |
| CoT-SC (k=100) | 9.0% |
| ToT (ours) (b=1) | 45% |
| ToT (ours) (b=5) | 74% |
表2：24点游戏结果对比。
2. 创意写作 (Creative Writing)
任务要求根据4个不相关的句子，创作一个连贯的四段式文章，并使每段分别以这四个句子结尾。
- 结果：ToT生成的文章在连贯性上表现更优。GPT-4自动评分中，ToT平均得分 7.56，高于CoT的6.93。在人类盲评中，41%的情况下人类偏好ToT的产出，而只有21%的情况偏好CoT。
- 方法：ToT在此任务中采用两步策略：首先生成多个写作计划并投票选出最佳计划，然后基于该计划生成多个段落并投票选出最终版本。这种“计划-执行”加“投票”的模式显著提升了全局连贯性。
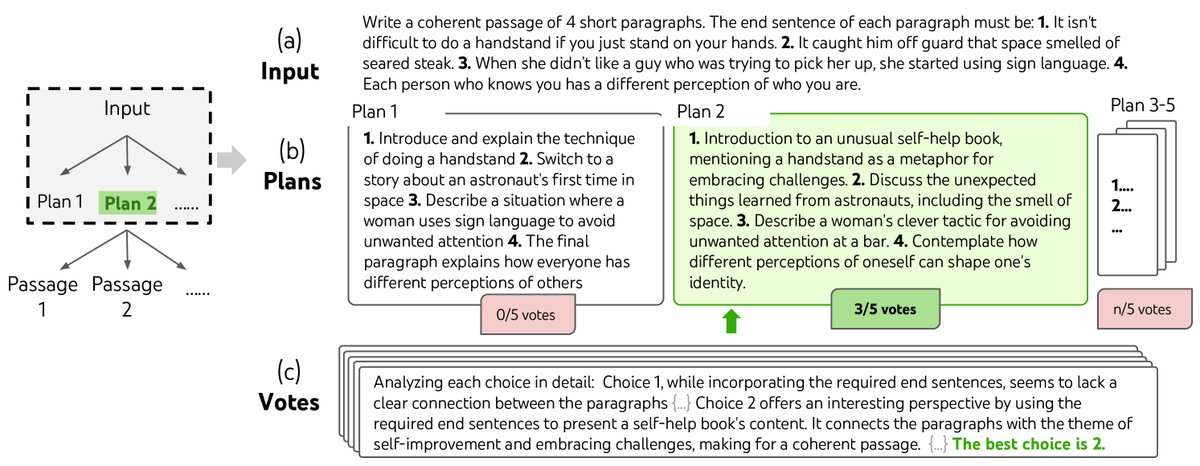图4：创意写作任务中的一步深思熟虑的搜索过程。LM首先采样5个不同的计划，然后投票选出最佳方案。
3. 迷你填字游戏 (Mini Crosswords)
这是一个5x5的填字游戏，需要根据横向和纵向的线索填充单词，是一个约束性很强的搜索问题。
- 结果：ToT的表现远超基线。在单词级别的正确率上，ToT达到 60%，而IO和CoT方法均低于16%。ToT成功解决了20个游戏中的4个，而CoT只解决了1个。
- 分析：此任务证明了DFS和回溯的重要性。消融实验表明，移除剪枝（pruning）或回溯（backtracking）机制都会导致性能大幅下降。这说明在复杂的组合空间中，有效的搜索策略至关重要。
| 方法 | 成功率 (%) - 字母/单词/游戏 |
|---|---|
| IO | 38.7 / 14 / 0 |
| CoT | 40.6 / 15.6 / 1 |
| ToT (ours) | 78 / 60 / 20 |
表3：迷你填字游戏结果。
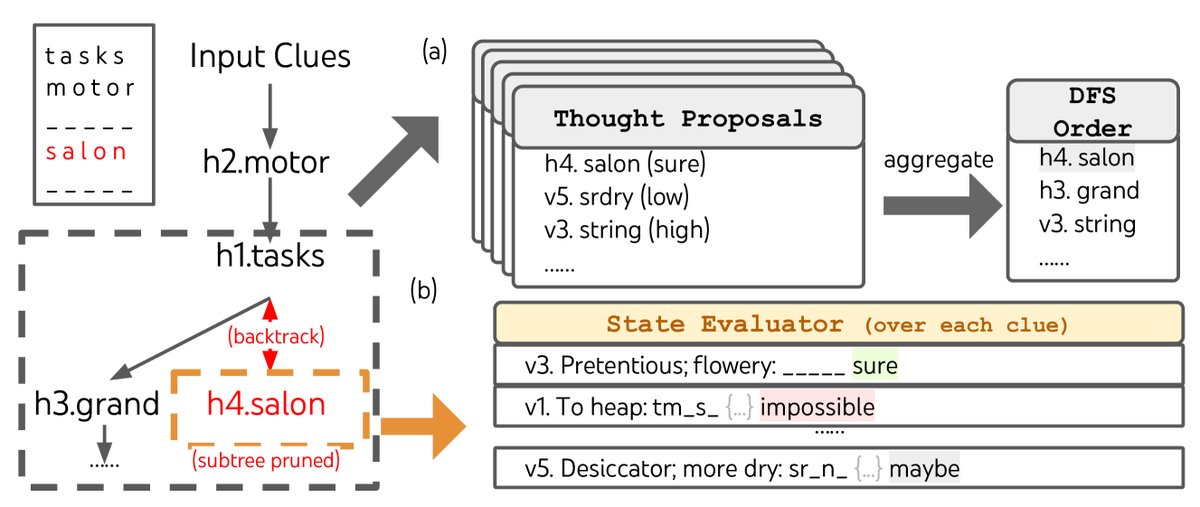图6：在迷你填字游戏中，(a) 思想被提出并放入优先队列进行DFS搜索，(b) LM评估一个状态是否可行，如果某个线索被判定为“不可能”填入，则进行剪枝并回溯。
总结
实验结果清晰地表明，ToT框架通过引入显式的搜索、规划、前瞻和回溯机制，并利用LM自身的推理能力进行启发式评估，能够在需要深思熟虑的问题解决任务上，显著超越传统的、线性的生成方法。