Uncovering Scaling Laws for Large Language Models via Inverse Problems

• ArXiv URL: http://arxiv.org/abs/2509.07909v1

• 作者: Bryan Kian Hsiang Low; Xinyuan Niu; Rui Qiao; See-Kiong Ng; Nhung Bui; Zi-Yu Khoo; Zitong Zhao; Jingtan Wang; Xiaoqiang Lin; Xinyi Xu; 等18人

• 发布机构: AI Singapore; Agency for Science, Technology and Research; CNRS@CREATE; National University of Singapore; SAP; Singapore-MIT Alliance for Research and Technology

---

TL;DR

本文倡导将大型语言模型（LLM）的开发挑战构建为逆问题（inverse problems），从而以一种系统性的、高成本效益的方式，发现指导LLM构建与优化的底层缩放定律（scaling laws）。

关键定义

本文的核心是提出一个概念框架，其关键定义如下：

• 正向过程 (Forward Process)：指代构建和评估LLM的标准流程。它包含两个阶段：
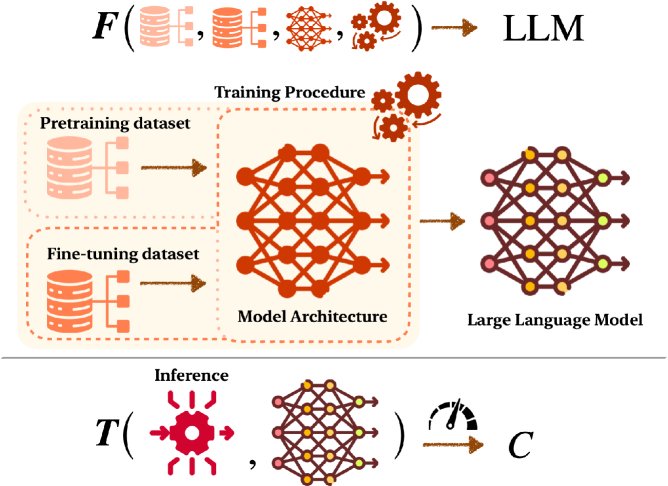
  1. 模型创建：使用训练要素 $\mathcal{T}$（包括数据集、模型架构、训练程序）通过计算过程 $\mathbf{F}$ 创建一个LLM实例。形式化为：$\mathbf{F}!\left(\mathcal{T}\right)\rightarrow\operatorname*{LLM}$。
  2. 模型评估：使用特定的推理方案要素 $\mathcal{I}$（如提示方法）在某个任务上评估该LLM，得到一个性能指标 $C$。形式化为：$\mathbf{T}!\left(\mathbf{F}!\left(\mathcal{T}\right),\mathcal{I}\right)\rightarrow C$。
• 逆问题 (Inverse Problem)：与正向过程相反，逆问题旨在从一个期望的性能结果 $C$ 出发，反向推断出实现该结果所需的最佳或最小输入要素（$\mathcal{T}$ 和 $\mathcal{I}$）。这是一个从“结果”反推“原因”的过程，目的是找到构建高性能、高效率LLM的最优配方，而不是通过昂贵的试错法。

相关工作

当前，大型语言模型（LLM）在各个领域取得了巨大成功，这些成功建立在空前的数据和计算规模之上。训练一个顶尖的LLM（如GPT-4）成本高达数亿美元，这使得通过“暴力试错”来改进模型变得不切实际。尽管已有研究揭示了模型性能与数据量、模型大小之间的部分缩放定律，但这些定律主要基于经验观察，且我们对数据、架构、训练和推理等多种要素之间复杂的相互作用仍缺乏深刻理解。

本文旨在解决的核心问题是：如何超越成本高昂的试错法，建立一个系统性的框架来发现指导LLM开发的基本定律？受到科学史上通过逆问题发现基本物理定律（如开普勒定律、牛顿万有引力定律）的启发，本文主张运用逆问题的思想来揭示LLM背后的缩放定律，从而以更高的成本效益实现理想的模型性能。

为此，本文将LLM的构建与评估流程形式化为两个正向过程：

	$\mathbf{F}!\left(\mathcal{T}\right)\rightarrow\operatorname*{LLM}\ ,$		(1a)
	$\mathbf{T}!\left(\mathbf{F}!\left(\mathcal{T}\right),\mathcal{I}\right)\rightarrow C\ .$		(1b)

其中，$\mathcal{T}$ 是训练要素，$\mathcal{I}$ 是推理要素，$C$ 是性能指标。逆问题就是要找到最优的 $\mathcal{T}$ 和 $\mathcal{I}$ 以达到特定的 $C$。

本文方法

本文的核心方法论是将LLM研究中的关键挑战重新构建为逆问题。通过固定部分变量，将复杂的端到端问题分解为更易于处理的子问题。本文重点阐述了三个领域的应用：数据选择、推理优化和机器学习遗忘。

数据选择

数据选择被构建为一个逆问题，目标是找到实现特定性能指标 $C$ 所需的最优或最小训练数据集（$\mathcal{T}$ 的一部分），从而发现数据量与模型性能之间的缩放关系。

• 多模态LLM的数据选择：多模态LLM (MLLM) 的指令微调（instruction-tuning）数据集常包含低质量和冗余数据。如何为MLLM高效选择同时考虑图像和文本特征的数据是一个挑战。逆问题的目标是识别出能超越传统幂律缩放的数据选择技术，并探索不同模态对性能影响的差异，最终发现适用于所有模态的通用缩放定律。

• 不可微性能指标下的数据选择：许多实用的LLM评估指标，如BLEU分数和LLM-as-a-judge，是不可微的，导致传统的基于梯度的数据选择方法失效。本文提倡研究如何在使用这些指标时进行数据选择，一个有前景的方向是利用强化学习（如REINFORCE算法）来估计不可微指标的“梯度”，从而直接优化目标。

• LLM对齐的数据选择：为了使LLM与人类意图对齐，通常采用基于人类反馈的强化学习（RLHF）或直接偏好优化（DPO）。这个过程高度依赖昂贵的人类反馈。该逆问题旨在设计一种有理论依据的主动学习策略，以最少的人类反馈量高效选择需标注的LLM响应，从而有效进行对齐训练。

• 联合优化：模型性能是多个训练阶段（如持续预训练、指令微调）共同作用的结果。因此，需要联合优化不同阶段的数据配比，乃至联合选择数据和模型架构，以发现它们共同影响模型性能的更深层次的缩放定律。

推理优化

推理优化被视为一个逆问题，目标是在给定已训练模型 $\mathbf{F}!\left(\mathcal{T}\right)$ 的情况下，设计最优的推理方案 $\mathcal{I}$，以达到期望的性能 $C$。

• 推理时数据优化：上下文学习（In-context learning）的效果极大程度上受提示（Prompt）中的指令和范例（exemplars）影响。该逆问题旨在资源受限（如计算或查询次数有限）的情况下，高效地自动优化提示内容。本文提出可将其建模为黑盒优化问题，并使用NeuralUCB等算法来求解，从而发现范例数量与模型性能之间的缩放关系。此外，还可扩展到依赖人类偏好反馈的提示优化。

• 推理时模型优化：在资源受限的部署场景中，如何选择最优的模型配置至关重要。这可以从两个角度解决：一是从不同规模的LLM中动态选择最合适的模型；二是在混合专家模型（Mixture-of-Experts, MoE）中确定推理时激活的最优专家数量，以平衡效率与性能。

• 推理时计算优化：链式思维（Chain of Thought, CoT）等技术表明，增加推理时的计算量可以提升性能。逆问题的目标是在固定的计算预算内，优化多种推理方案（如CoT、检索增强生成、集成等）的组合，以发现更有效的性能-计算缩放行为。

• 推理时联合优化：LLM的最终表现是数据、模型和计算三者相互作用的结果。因此，需要研究如何联合优化模型配置和推理方案，在固定的计算成本下实现最佳性能，这将揭示它们共同影响性能的缩放定律。

机器学习遗忘

机器学习遗忘（Machine Unlearning, MU）旨在从模型中移除特定训练数据的影响。本文从两个角度将其构建为逆问题。

• 机器学习遗忘验证：验证是一个逆问题，即给定一个声称“已遗忘”的模型，判断其训练要素 $\mathcal{T}$ 中是否还包含被删除的数据。传统方法需要重新训练模型，成本高昂。本文提出了一种新的思路：在训练前为数据嵌入独特的水印（watermarking），通过检测遗忘后模型生成内容中是否还存在水印来验证遗忘效果。这将有助于建立一个无需重训练的、高效的验证指标，并研究遗忘难度与数据属性之间的缩放关系。

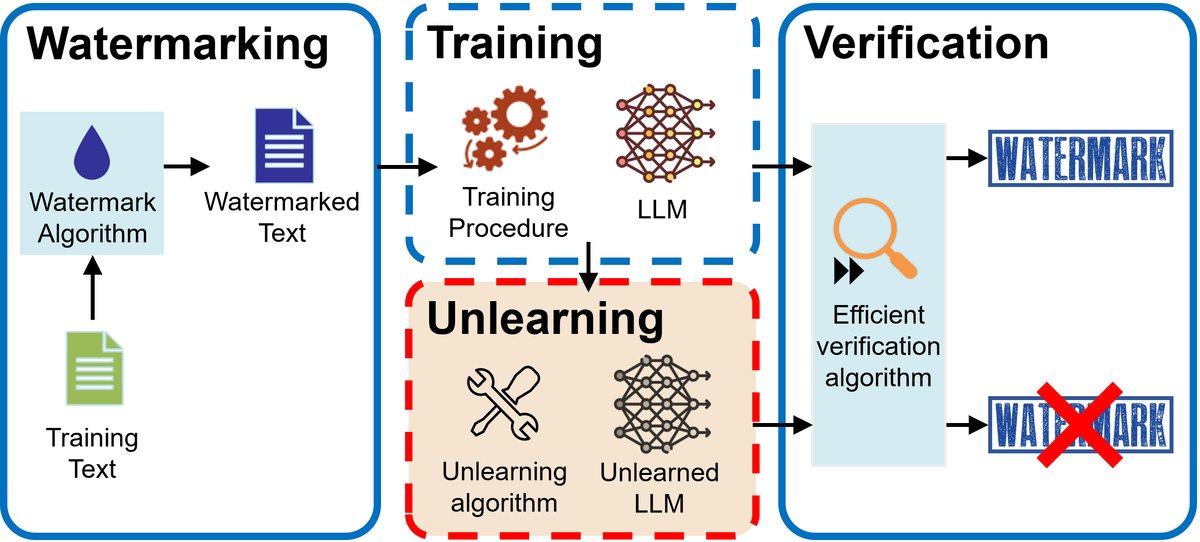
• 机器学习遗忘技术：MU技术本身也是一个逆问题，目标是调整训练要素 $\mathcal{T}$ 或推理要素 $\mathcal{I}$，以达到期望的性能指标 $C$（如：不生成有害内容、在保留数据上性能不下降）。对于黑盒模型，可以在推理时自适应地修改 $\mathcal{I}$ 来抑制有害内容的生成。对于白盒模型，可以设计更易于遗忘的模型架构（如MoE），仅对少数参数进行修改。研究这些技术与遗忘效果、数据大小、计算成本之间的关系，可以揭示指导MU实践的缩放定律。

实验结论

本文是一篇立场文件（position paper），旨在提出一个概念框架，并未包含具体的实验验证。其核心结论是，将LLM开发中的挑战（如数据选择、推理优化、机器学习遗忘等）系统地构建为逆问题，是一种极具前景的研究范式。这一方法论有望引导研究从零散的经验性改进转向对底层缩放定律的探索，从而为构建更强大、更高效、更安全的LLM奠定理论基础，并指导实际应用中的资源优化。未来的研究应致力于探索这些缩放定律，并利用优化理论等领域的工具来解决LLM中的逆问题。