Understanding R1-Zero-Like Training: A Critical Perspective

ArXiv URL: http://arxiv.org/abs/2503.20783v1
作者: Wenjun Li; Chao Du; Changyu Chen; Penghui Qi; Min Lin; Tianyu Pang; Wee Sun Lee; Zi-Yan Liu
发布机构: National University of Singapore; Sea AI Lab; Singapore Management University

TL;DR

本文通过剖析 R1-Zero 类训练，揭示了其基座模型与强化学习算法（GRPO）中存在的偏见，并提出了一种无偏的优化方法 Dr. GRPO，从而以更高效的方式提升了模型的数学推理能力。

关键定义

R1-Zero 类训练 (R1-Zero-like training): 一种大语言模型（LLM）的后训练范式，其核心特点是跳过监督微调（SFT）步骤，直接对基座模型应用强化学习（RL）来提升特定能力（如推理）。
Aha 时刻 (Aha moment): 指模型在训练过程中涌现出自我反思、修正错误等高级推理行为的现象。本文发现，这种行为在许多基座模型中（包括 DeepSeek-V3-Base）在强化学习训练前就已存在。
GRPO (Group Relative Policy Optimization): 一种用于大模型强化学习的策略优化算法。它通过对每个问题采样一组回答，并根据这组回答的平均和标准差来计算优势函数（advantage），其计算方式为 $(奖励 - 组内平均奖励) / 组内奖励标准差$。
Dr. GRPO (GRPO Done Right): 本文提出的 GRPO 改进版本。它通过移除 GRPO 优势函数计算中的长度归一化和标准差归一化项，修正了原算法中存在的优化偏见，是一种更简洁、无偏的优化方法。

本文方法

本文从基座模型和强化学习算法两个方面对 R1-Zero 类训练进行了批判性分析，并提出了一种名为 Dr. GRPO 的无偏见优化算法。

对基座模型的分析

研究发现，基座模型的预训练特性对 R1-Zero 类训练的结果有深远影响。

模板的重要性与 Qwen 模型的特殊性: 对于多数纯基座模型（如 Llama、DeepSeek），使用合适的提示模板（template）是诱导其从“续写”模式切换到“问答”模式的关键。然而，一个有趣的发现是，Qwen2.5 系列模型在不使用任何模板的情况下表现出最强的推理能力。这暗示 Qwen2.5 在预训练阶段可能已经接触过“问题-答案”配对的文本格式，使其更像一个经过微调的模型，而非纯粹的基座模型。

基座模型 + 模板	AIME24	AMC	MATH500	Minerva	OlympiadBench	平均值
Qwen2.5-Math-1.5B
(4-shot prompting)	0.0	20.0	50.4	12.1	15.9	19.7
R1 template	0.0	9.6	21.2	6.6	2.2	7.9
Qwen template	20.0	32.5	33.0	12.5	22.8	24.2
无模板	16.7	43.4	61.8	15.1	28.4	33.1
Qwen2.5-Math-7B
(4-shot prompting)	3.3	22.5	61.6	10.7	20.9	23.8
R1 template	0.0	0.0	0.0	0.0	0.1	0.0
Qwen template	16.7	38.6	50.6	9.9	16.6	26.5
无模板	0.2	45.8	69.0	21.3	34.7	38.2

“Aha 时刻”并非 RL 涌现: 通过对包括 DeepSeek-V3-Base 在内的多个基座模型进行测试，本文发现“Aha 时刻”（如生成“等等”、“让我想想”、“验证一下”等自我反思关键词）在强化学习开始之前就已经普遍存在于基座模型中。这表明，该现象并非纯粹由强化学习过程涌现，其根源可能在于预训练数据。

Figure 4: Cases showing that DeepSeek-V3-Base already exhibits “Aha moment” even before RL tunning.

对强化学习算法的分析与 Dr. GRPO

本文对 GRPO 算法进行了深入分析，并指出了其固有的优化偏见。

创新点：识别 GRPO 的优化偏见

GRPO 的 PPO 风格目标函数为：

\[\mathcal{J}_{GRPO}(\pi_{\theta})=\mathbb{E}_{\mathbf{q}\sim p_{\mathcal{Q}},\{\mathbf{o}_i\}_{i=1}^{G}\sim\pi_{\theta_{old}}(\cdot \mid \mathbf{q}})} \frac{1}{G}\sum_{i=1}^{G}{\color[rgb]{1,0,0}\frac{1}{ \mid \mathbf{o}_i \mid }}\sum_{t=1}^{ \mid \mathbf{o}_i \mid }\left\{\dots\right\}\]

其优势函数（advantage）$\hat{A}_{i,t}$ 计算为：

\[\hat{A}_{i,t}=\frac{R(\mathbf{q},\mathbf{o}_i)-\operatorname{mean}({\{R(\mathbf{q},\mathbf{o}_1),\dots,R(\mathbf{q},\mathbf{o}_G)\}})}{{\color[rgb]{1,0,0}\operatorname{std}({\{R(\mathbf{q},\mathbf{o}_1),\dots,R(\mathbf{q},\mathbf{o}_G)\}})}}\]

本文指出，公式中红色部分引入了两种偏见：

响应级长度偏见 (Response-level length bias): 由损失函数中的 $$1/

o_i

$$ 项引入。对于奖励为正的正确回答，该项会给予较短的回答更大的梯度更新，鼓励模型生成简短的正确答案。但对于奖励为负的错误回答，该项会减少对较长回答的惩罚，导致模型在犯错时倾向于生成越来越长的无效思考过程。

问题级难度偏见 (Question-level difficulty bias): 由优势函数中按问题（per-question）计算的 $std(...)$ 分母引入。对于奖励方差很小的问题（即太容易或太难，导致模型回答几乎全对或全错），该项会给予过大的权重，而在中等难度问题上权重较小，从而扭曲了优化方向。

Figure 5: Illustration of the biases in GRPO.

Dr. GRPO: 无偏见的优化方法

为了解决上述偏见，本文提出了 Dr. GRPO。其核心改动非常简单：移除引入偏见的两项归一化，即去掉损失函数中的 $1/|o_i|$ 和优势函数计算中的 $std(...)$ 分母。

Figure 1: Left: Dr. GRPO introduces simple yet significant modifications to address the biases in GRPO, by removing the length and std normalization terms. Right: Our unbiased optimizer effectively prevents the model from generating progressively longer incorrect responses, thereby enhancing token efficiency.

优点

Dr. GRPO 作为一个无偏见的优化器，带来了显著的好处：

提升Token效率: 通过消除长度偏见，Dr. GRPO 有效地阻止了模型在训练过程中生成越来越长的错误答案，避免了不必要的“过度思考”，从而提高了 token 的使用效率。
保持推理性能: 在提升效率的同时，Dr. GRPO 能够达到与原版 GRPO 相当甚至更好的推理性能。
原理更简洁: 移除不必要的归一化项后，Dr. GRPO 的形式回归到标准的 PPO 目标，使用了带无偏基线（unbiased baseline）的蒙特卡洛回报来估计优势，理论上更加稳固。

实验结论

本文通过一系列实验验证了其分析和方法的有效性。

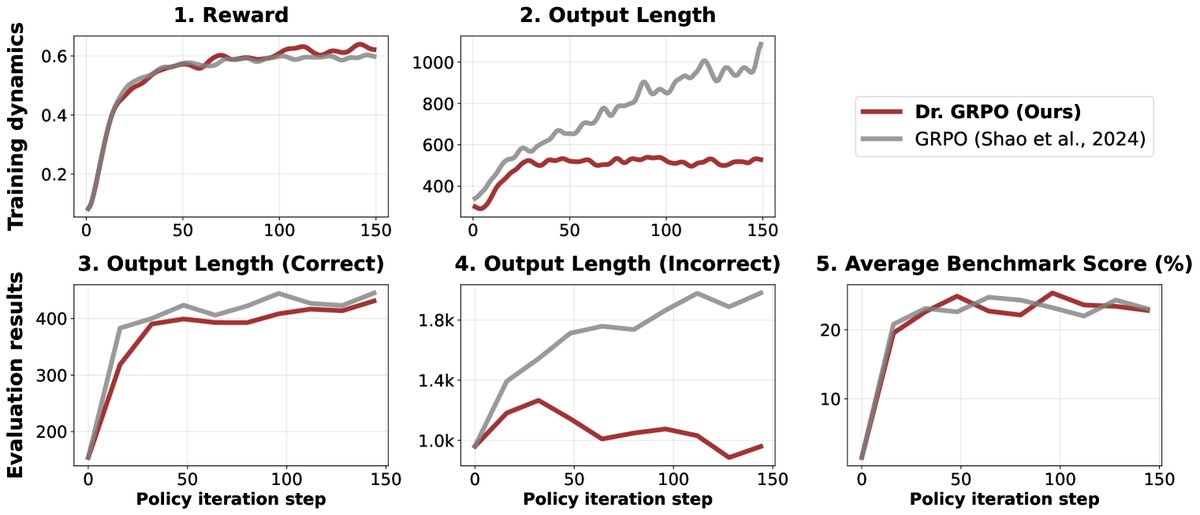
Dr. GRPO vs. GRPO: 对比实验表明，GRPO 训练的模型在奖励增长放缓后，其错误回答的长度仍然持续增加，证实了长度偏见的存在。而 Dr. GRPO 在达到相似性能的同时，显著缩短了错误回答的长度，提升了 token 效率。

Figure 6: Comparison of Dr. GRPO and GRPO in terms of training dynamics (Top) and evaluation results (Bottom).

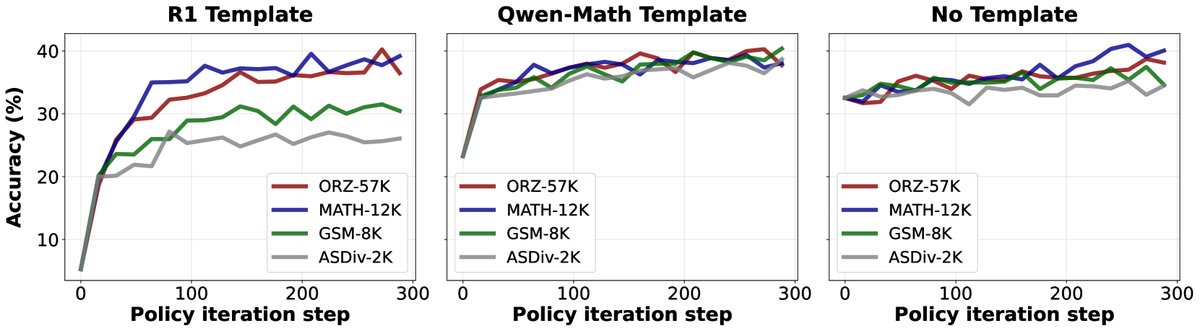
模板与训练数据的重要性: 实验显示，对于 Qwen2.5-Math 这种本身数学能力很强的模型，强化学习更像是在“重构”被不匹配模板破坏的能力，此时训练数据覆盖范围的影响较小。而对于需要从头学习的更“纯粹”的基座模型，强化学习依赖于覆盖良好、知识丰富的训练集。

Figure 7: The average benchmark accuracy of different {template, question set} combinations during RL training.

在弱基座模型上的应用: 实验证明，即使是数学能力较弱的基座模型（如 Llama-3.2），通过领域内的持续预训练，也能为后续的强化学习打下良好基础，并取得显著性能提升。这也再次验证了 GRPO 的偏见会导致模型长度不必要地增长，而 Dr. GRPO 可以修正这一问题。
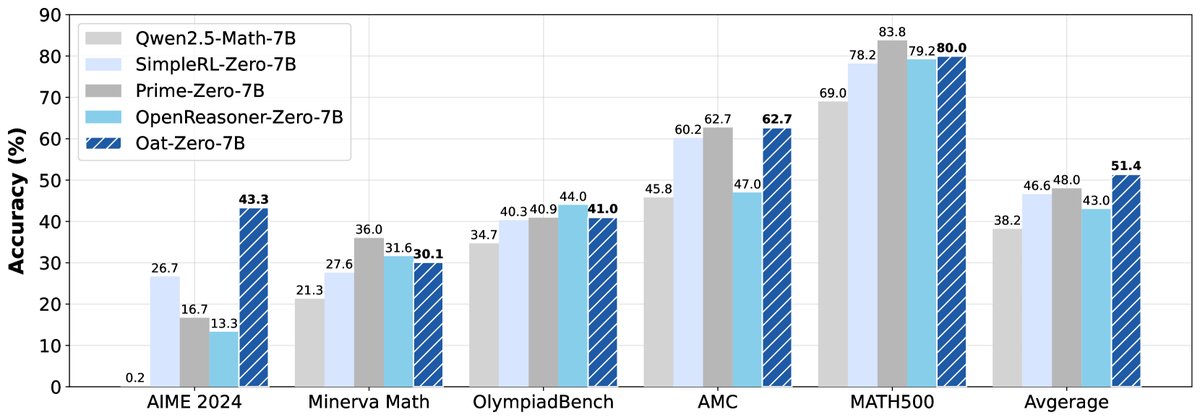
最终成果: 结合以上洞见，本文提出了一个极简的 R1-Zero 训练方案：使用 Qwen2.5-Math-7B 基座模型、无偏的 Dr. GRPO 算法、Qwen-Math 模板，在 MATH 数据集上进行训练。该方法仅用 8 卡 A100 训练 27 小时，就在 AIME 2024 测试集上达到了 43.3% 的准确率，为 7B 模型设立了新的技术水平。

Figure 2: Model performance comparison.