Understanding the Role of Training Data in Test-Time Scaling

ArXiv URL: http://arxiv.org/abs/2510.03605v1
作者: Baharan Mirzasoleiman; Adel Javanmard
发布机构: Google Research; University of California Los Angeles; University of Southern California

TL;DR

本文通过一个可理论分析的线性回归任务，从理论上解释了训练数据的特性如何决定测试时增加计算（即更长的思想链）能否成功提升模型性能，并证明了在多样化、相关且困难的任务上进行训练对测试时扩展（test-time scaling）最为有利。

关键定义

测试时扩展 (Test-time scaling): 在模型参数固定的情况下，于推理（测试）阶段分配额外的计算资源，例如生成更长的思想链 (Chain-of-Thoughts, CoT)，以解决更复杂的问题。
上下文权重预测 (In-context weight prediction): 本文研究的一种特定的上下文学习 (In-context learning, ICL) 任务。不同于预测单个输出 \(y\)，该任务要求模型直接从给定的上下文 \((x_i, y_i)\) 序列中，推断出背后隐藏的线性回归权重向量 \(w\)。
任务难度 (Task Hardness): 本文提出的一个量化指标，定义为 \(Hard(Λ) := tr(Λ) / λ_min(Λ)\)，其中 \(Λ\) 是任务特征的协方差矩阵，\(tr(Λ)\) 是其迹，\(λ_min(Λ)\) 是其最小特征值。该指标衡量了学习任务所需“技能”的多样性和不均衡性，数值越高意味着任务越难。

本文方法

理论框架：线性回归中的上下文学习

本文在一个简化的、可分析的环境中研究测试时扩展：针对线性回归任务的上下文权重预测。

1. 任务设置：模型接收一个由多个 \((特征, 标签)\) 对组成的提示 (prompt)，形如 \(P_τ = (x_{τ,1}, y_{τ,1}, ..., x_{τ,n}, y_{τ,n})\)，其中 \(y_{τ,i} = <w_τ, x_{τ,i}>\)。模型的目标是直接预测出隐藏的权重向量 \(w_τ\)。

2. 模型架构：采用一个仅包含单层线性自注意力 (Linear Self-Attention, LSA) 和残差连接的简化 Transformer 模型。其更新公式为：

\[\nf_{\mathrm{LSA}}(E;\theta)=E+VE\cdot\frac{E^{\top}WE}{\rho}\]

其中 \(E\) 是输入的嵌入矩阵，\(θ = (W, V)\) 是可学习参数。

3. 训练动态：本文证明，对于该设置下的总体损失函数，使用梯度下降法在合适的初始化条件下能够收敛到全局最优解，并给出了最优参数 \(W_*\) 和 \(V_*\) 的显式表达。训练过程中不使用CoT，模型直接进行权重预测。这为后续分析模型在测试时的行为奠定了基础。

创新点

测试时 CoT 的机制等价于优化算法

本文的核心洞见在于揭示了测试时 CoT 的数学本质。在测试时，模型被允许多次迭代生成中间结果。具体来说，模型在第 \(i\) 步的预测 \(w_i\) 会被加入到下一步的输入 \(E_i\) 中，形成一个迭代链条。

本文从理论上证明，这个迭代过程等价于一个多步（伪）牛顿法 (multi-step (pseudo-) Newton’s method)，用于优化线性回归的损失。每一步的权重更新遵循以下规则：

\[w_{i+1}=w_{i}-\frac{1}{m}\Gamma^{-1}X_{\rm test}X_{\rm test}^{\top}(w_{i}-w_{\rm test})\]

其中 \(Γ\) 是一个由训练数据分布决定的矩阵，\(X_test\) 是测试数据。这表明，CoT的每一步都是在利用模型从训练中学到的知识（体现在 \(Γ\) 中）来对权重 \(w\) 进行一次优化迭代。最终经过 \(k\) 步CoT后的预测误差会以指数形式衰减：

\[\operatorname{\mathbb{E}}(\left\ \mid w_{k+1}-w_{\rm test}\right\ \mid _{\ell_{2}}^{2})\leq d\left(1+\frac{n}{1+{\sf{Hard}}(\Lambda)}\right)^{-2k}(1+o(1))\]

这个公式清晰地表明，增加CoT步数 \(k\) 可以显著降低预测误差。

任务难度的量化与过思考现象的解释

基于误差分析，本文提出了任务难度的量化定义：

\[{\sf{Hard}}(\Lambda):=\frac{{{\operatorname{tr}}}(\Lambda)}{\lambda_{\min}(\Lambda)}\]

这个定义有一种直观的物理解释：协方差矩阵 \(Λ\) 的每个特征向量代表解决任务所需的一种“技能”，对应的特征值大小代表该技能在任务中的重要性或出现频率。一个“简单”任务可能只依赖少数几种主导技能（特征值谱衰减快），而一个“困难”任务则需要掌握大量长尾技能（存在很小的特征值），因此 \(Hard(Λ)\) 值更高。

误差公式表明，任务越难（\(Hard(Λ)\) 越大），误差衰减得越慢，需要更多的CoT步数 \(k\) 才能达到理想的精度。

此外，该框架也解释了“过度思考”现象：如果测试任务所需的某些“技能”（\(Λ_test\) 的某些特征方向）在训练数据（\(Λ_train\)）中没有得到充分体现，那么模型学到的 \(Γ\) 矩阵在这些方向上就是“盲区”。在这些方向上进行CoT迭代不仅没有帮助，反而会放大误差，导致性能下降。

最优任务选择策略

本文将理论扩展到多任务训练场景，目标是找到最优的任务选择概率 \({π_i}\)，使得模型在目标任务 \(Σ\)上表现最好。通过最小化测试误差的上界，本文推导出选择训练任务的三个核心原则：

多样性 (Diverse): 训练任务的组合 \(Σ_i π_i Λ_i\) 必须在特征空间上全面覆盖目标任务 \(Σ\) 的所有方向。否则，在未覆盖的方向上误差会很大。
相关性 (Relevant): 应优先选择与目标任务 \(Σ\) 更相似的训练任务 \(Λ_i\)，因为最终学到的能力是所有训练任务的加权组合。
困难度 (Hard): 当目标任务本身很困难时（通常是评测基准的情况），也必须在训练中包含足够困难的任务。这是因为只有困难的训练任务才能帮助模型学会应对那些罕见但关键的“长尾技能”。

为了便于实际操作，本文还提出了一个简化的凸二次规划问题来求解最优的任务选择概率 \({π_i}\)。

实验结论

本文通过在 LSA 模型和更复杂的 GPT-2 模型上进行实验，验证了其理论发现。

测试计算可换取训练数据：实验表明，增加测试时的CoT步数 \(k\)，可以在达到相同测试误差的前提下，减少训练时所需的上下文长度 \(n\)。这证实了测试时计算与训练数据量之间存在权衡关系。
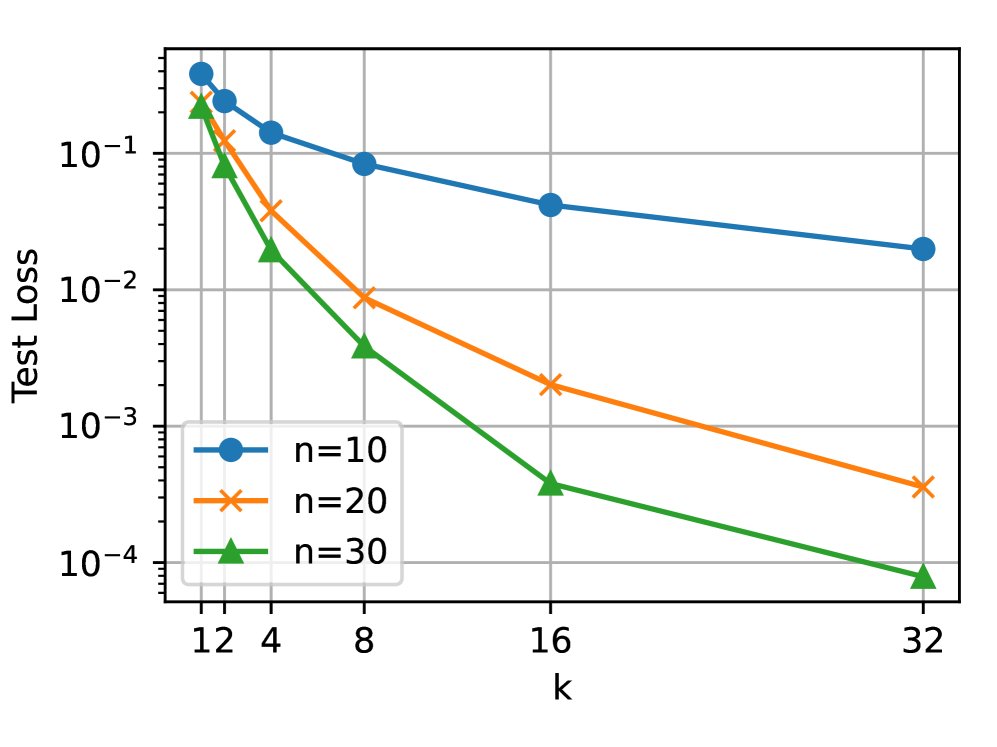
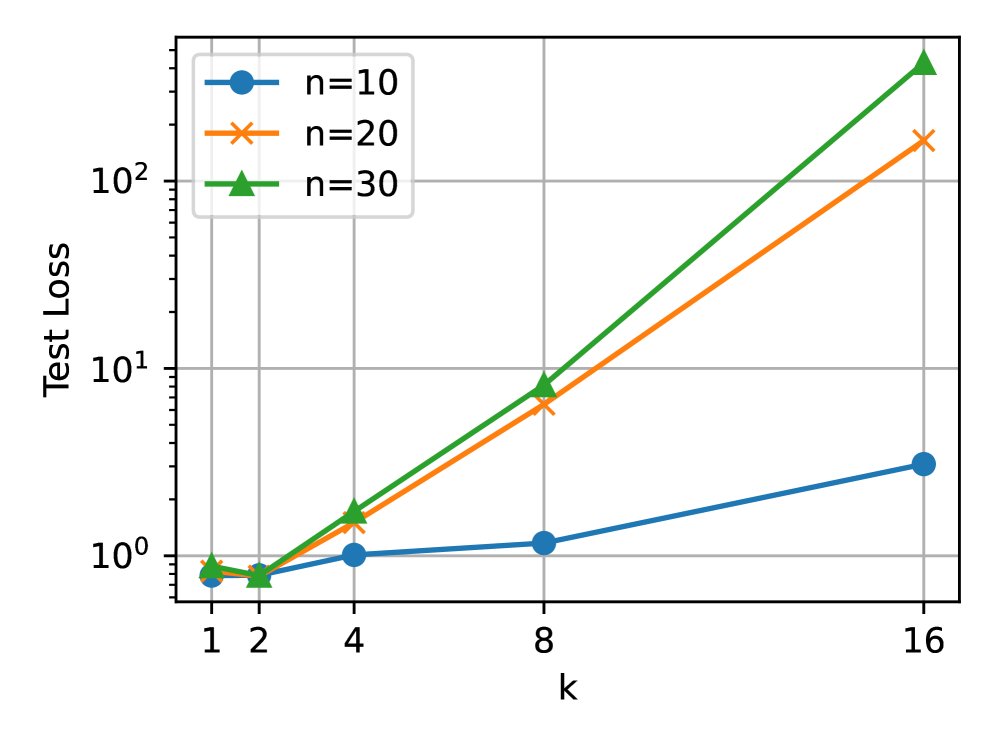
“过度思考”现象的复现：当训练数据（特征协方差矩阵 \(Λ\) 倾斜）与测试数据（单位矩阵 \(I_d\)）分布不匹配时，即训练数据无法覆盖测试任务所需的所有技能时，增加CoT步数 \(k\) 会导致测试误差上升，即出现“过度思考”。这与理论预测完全一致。
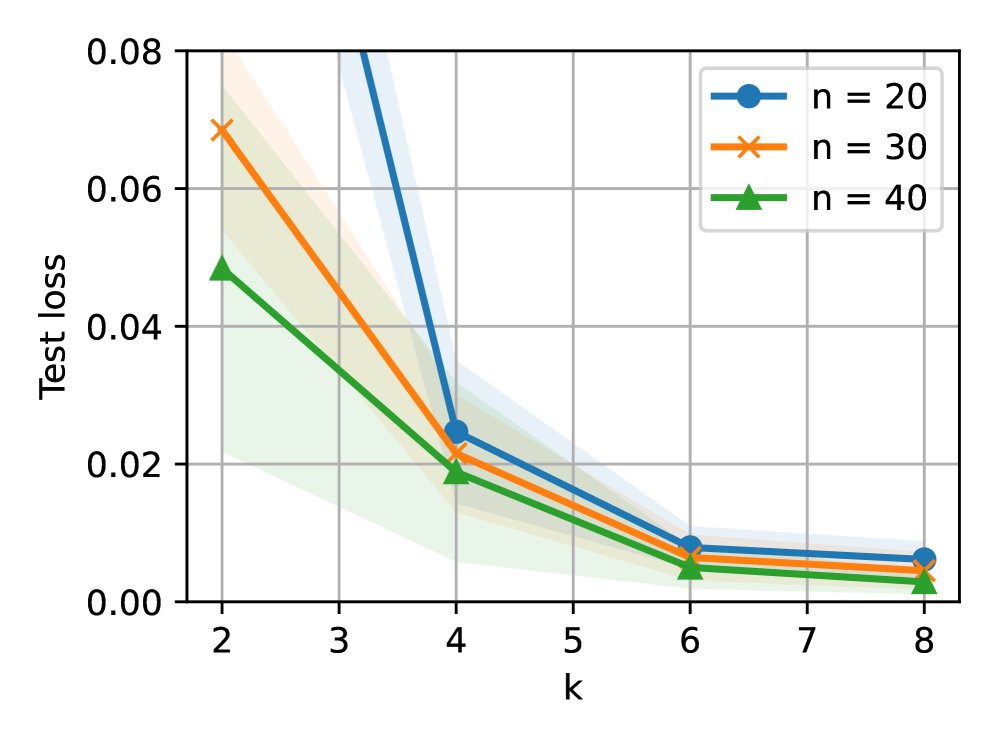
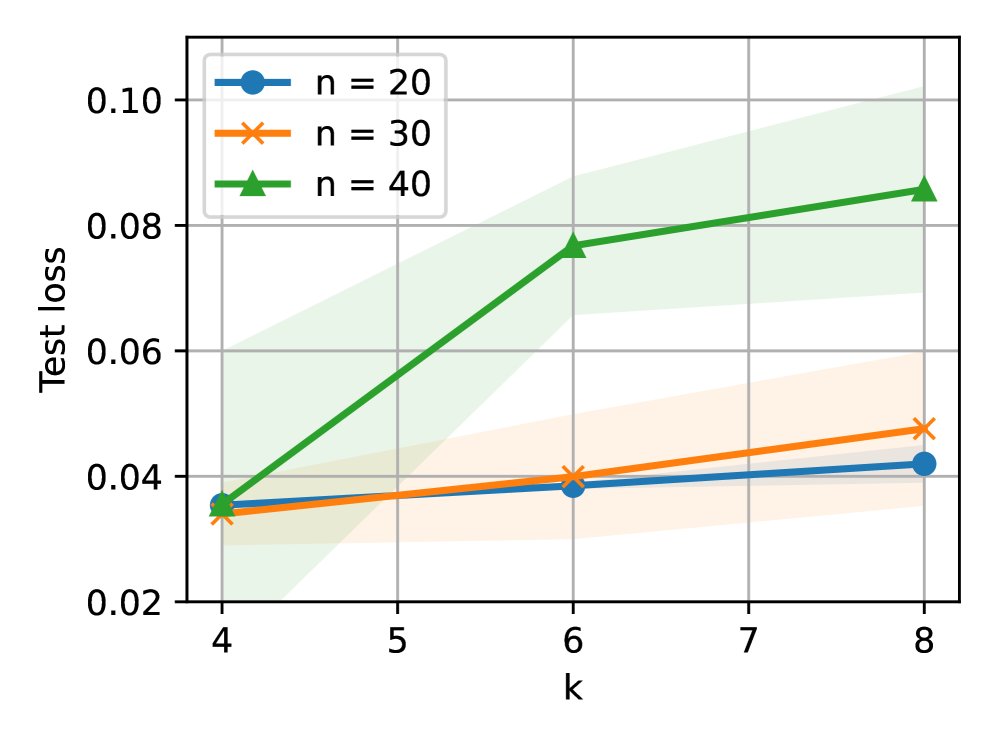
任务选择策略的验证：在多任务实验中，本文提出的优化方法能够自动选择多样化且困难的任务进行训练。与均匀选择或仅选择简单/相关任务相比，该策略训练出的模型在困难的下游任务上表现出最佳的测试时扩展能力。

最终结论：本文的理论和实验共同证明，测试时扩展的成功并非偶然，它深刻地依赖于训练数据的多样性、相关性和难度。只有当训练数据充分覆盖了测试任务所需的“技能”时，增加CoT步数才能像优化算法一样逐步逼近正确答案；否则，模型就会“过度思考”并导致性能下降。因此，精心设计和组合训练任务是释放模型推理潜力的关键。