Valid Survey Simulations with Limited Human Data: The Roles of Prompting, Fine-Tuning, and Rectification

ArXiv URL: http://arxiv.org/abs/2510.11408v1
作者: Giuseppe Russo; Robert West; Kristina Gligorić; Serina Chang
发布机构: EPFL; Johns Hopkins University; Stanford University; University of California, Berkeley

TL;DR

本文提出了一种将大型语言模型（LLM）用于调查问卷模拟的有效框架，其核心思想是：不应将所有宝贵的人类数据用于微调模型，而应将大部分数据用于对LLM生成的大量合成数据进行统计校正（Rectification），从而在有限的人类数据下获得低偏倚、高效率的群体估计。

关键定义

本文的核心在于结合以下两种方法，并探讨了它们之间的数据分配策略：

合成 (Synthesis)：指使用大型语言模型（LLM）来生成调查问卷的响应。本文中，合成策略主要分为两类：
- 基于提示 (Prompt-based)：在推理时通过特定的提示词（如人口统计信息或基于历史行为生成的“人格”画像）来引导模型生成响应，无需更新模型参数。
- 基于微调 (Fine-tuning)：使用一部分人类调查数据对LLM进行监督式微调，以使其更好地适应特定领域或人群。
校正 (Rectification)：一种后处理（post-hoc）的统计方法，旨在修正由LLM合成数据所产生的估计偏差。它利用一小部分真实的人类响应数据，与大量的、廉价的LLM合成响应相结合，以得出一个更准确的群体参数估计值。本文中，该方法以 PPI (Prediction-Powered Inference) 框架为基础。
有效样本量增益 (Effective Sample Size, ESS Gain)：一个衡量方法效率的指标，用于量化校正方法相比于仅使用人类小样本进行估计所带来的方差缩减程度。例如，50%的ESS增益意味着该方法的估计精度等同于多收集了50%的人类样本。

本文方法

本文将调查模拟构建为一个两阶段的框架：合成-校正 (Synthesis-Rectification)。其目标是利用少量人类数据和一个仅包含人口统计信息的大规模数据集，准确估计目标群体的统计参数（如均值）。

框架图上图展示了本文提出的框架。首先，利用一个小型人类数据集 $(X^{n},Y^{n})$ 和一个大型 demographics-only 数据集 $X^{N}$，通过提示或微调生成合成响应 $\hat{Y}^{n}$ 和 $\hat{Y}^{N}$。接着，结合模型在人类样本上的预测 $\hat{Y}^{n}$ 和真实响应 $Y^{n}$ 计算一个校正项。最后，将此校正项与在大规模数据集上的合成响应 $\hat{Y}^{N}$ 结合，得出最终的群体估计值 $\hat{\theta}$ 及其置信区间。

问题形式化

假设一个调查在 $T$ 个时间点（波次）对 $N$ 个个体进行。在第 $T$ 波，本文旨在使用LLM $f$ 基于个体的协变量 $\mathbf{x}_{i}$ 和历史响应 $y_{i,1:T-1}$ 来生成合成响应：

\[\hat{y}_{i,T} = f(\mathbf{x}_{i}, y_{i,1:T-1})\]

目标是估计在第 $T$ 波的总体参数 $\theta^{*}$，定义为总体均值：

\[\theta^{\ast} := \frac{1}{N}\sum_{i=1}^{N}\phi(y_{i,T})\]

其中 $\phi$ 是一个将响应映射到实数值的函数。

合成 (Synthesis)

本文评估了四种不同的LLM响应合成策略：

Demo-Prompt: 仅使用人口统计学信息 $\mathbf{x}_{i}$ 作为提示。
Persona-Prompt: 使用一个辅助LLM分析个体的历史响应 $y_{i,1:T-1}$，生成一段描述其行为模式的自然语言“人格”画像，再结合人口统计信息进行提示。
FT-History: 使用目标调查的历史数据（第 $1$ 到 $T-1$ 波）对LLM进行监督式微调。
FT-SubPOP: 使用一个外部的大型调查数据集 (SubPOP)，该数据集包含不同子群体的响应分布，通过最小化模型预测分布与真实分布之间的KL散度来进行微调。

校正 (Rectification)

尽管合成为我们提供了大量的低成本响应，但这些响应存在偏差。校正步骤利用一小部分（$n$个）真实的人类响应 $\mathcal{H}={(\mathbf{x}_{j},y_{j})}_{j=1}^{n}$ 来纠正这种偏差。通用的校正估计器形式如下：

\[\hat{\theta}_{\lambda}=\underbrace{\frac{1}{N}\sum_{i=1}^{N}\lambda\,\hat{y}_{i}}_{\text{synthetic mean}}+\underbrace{\frac{1}{n}\sum_{j=1}^{n}\bigl(y_{j}-\lambda\,\hat{y}_{j}\bigr)}_{\text{bias correction}}\]

其中，$\lambda \in [0,1]$ 是一个“功率调节”参数。

当 $\lambda=1$ 时，该估计器等价于DSL方法（本文称为 $\text{Rec}_{\lambda=1}$）。
本文主要采用PPI++的策略，通过最小化估计方差来自动选择最优的 $\lambda$（称为 $\text{Rec}_{\lambda_{\text{opt}}}$）。

创新点

本文的核心创新并非提出一个全新的模型，而是系统性地评估了合成与校正相结合的框架，并揭示了其中关键的权衡关系。

挑战传统认知：本文有力地挑战了“将所有可用的人类数据都用于微调模型是最佳选择”这一普遍认知。
提出数据分配策略：通过实验证明，在固定的数据预算下，将一小部分数据用于微调（以提高模型预测与真实响应的相关性），而将大部分数据保留用于后处理校正，是实现最低偏倚和最高效率（即最低方差）的最佳策略。
方差缩减的理论支撑：该框架的有效性根植于其方差特性。校正后估计器的方差为：
\[\operatorname{Var}(\hat{\theta}_{\lambda})=\frac{\lambda^{2}\operatorname{Var}(\haty)}{N}+\frac{\operatorname{Var}(y-\lambda\,\hat{y})}{n}\]
当模型精度足够高（即误差方差 $\operatorname{Var}(y-\lambda\haty)$ 较小）且合成样本量 $N$ 足够大时，该方法的总方差可以远小于仅依赖 $n$ 个人类样本的估计方差（$\frac{\operatorname{Var}(y)}{n}$），从而实现有效样本量（ESS）的显著增益。

实验结论

本文在两个大型纵向调查（NHANES关于营养摄入，ATP关于政治经济观点）上进行了广泛实验，涵盖了开放式和多项选择题两种格式。

不同方法的偏倚和效率

实验结果清晰地表明了合成与校正结合的优越性。

纯合成方法偏倚巨大：单独使用任何一种LLM合成策略（不加校正）都会产生巨大的偏倚（平均24%–86%），且结果在不同数据集和方法间极不稳定，这证明了纯LLM模拟的不可靠性。
校正显著降低偏倚：应用校正后，特别是使用最优功率调节的 $\text{Rec}_{\lambda_{\text{opt}}}$，所有方法的偏倚都大幅降低到5%以下。其中，基于微调的合成方法（$FT-History$ 和 $FT-SubPOP$）与校正结合后表现最佳，平均偏倚低于3%，且在所有数据集上偏倚均不具备统计显著性。
校正提升估计效率：所有未经校正的方法都无法达到名义上的置信区间覆盖率。然而，一旦与 $\text{Rec}_{\lambda_{\text{opt}}}$ 结合，所有方法都获得了正的ESS增益（最高达14.19%），这意味着该组合方法比仅使用人类小样本得到了更精确的估计（即更低的方差）。

下表总结了在$n_{\text{human}}=100$的情况下，不同合成与校正方法组合的性能表现（偏倚%和ESS增益%）。

方法	模型	NHANES (食物)	ATP Q1 (经济)	ATP Q2 (政治)	平均
		偏倚% (ESS%)	偏倚%(ESS%)	偏倚%(ESS%)	偏倚%(ESS%)
无校正
基线	-	24.11	-	62.41	43.26
Demo-Prompt	Llama 3.1 8B	41.52 $\dagger$	32.22 $\dagger$	30.25 $\dagger$	34.66 $\dagger$
Persona-Prompt	Llama 3.1 8B	60.15 $\dagger$	72.15 $\dagger$	19.99 $\dagger$	50.76 $\dagger$
FT-History	Llama 3.1 8B	58.75 $\dagger$	86.85 $\dagger$	21.20 $\dagger$	55.60 $\dagger$
FT-SubPOP	Llama 3.1 8B	148.9 $\dagger$	31.54 $\dagger$	78.27 $\dagger$	86.23 $\dagger$
有校正
Rec$_{\lambda_{opt}}$
Demo-Prompt	Llama 3.1 8B	4.30 (13.79)	4.41 (2.53)	2.50 (2.57)	3.74 (6.30)
Persona-Prompt	Llama 3.1 8B	6.70 (11.66)	5.51 (2.59)	4.31 (3.30)	5.51 (5.85)
FT-History	Llama 3.1 8B	2.45 (14.19)	3.49 (2.42)	1.54 (4.15)	2.49 (6.92)
FT-SubPOP	Llama 3.1 8B	2.82 (12.59)	3.82 (2.61)	3.72 (1.09)	3.45 (5.43)

$\dagger$ 表示由于未校正方法的置信区间未能达到名义覆盖率，ESS增益无意义。绿色表示偏倚的95%置信区间包含0且ESS>0。

子群体效应与分配策略

子群体偏倚：本文进一步分析了校正对不同人口子群体的影响。结果显示，全局的校正方法也能大致降低大多数子群体的估计偏倚，尽管对个别群体可能效果不一。这表明校正有助于缓解不同群体间的性能差异。

子群体	N	微调后偏倚 (%)	校正后偏倚 (%)	变化
总人口	7027	7.93	2.45	💚
性别: 女性	3608	4.62	7.32	💔
性别: 男性	3419	13.86	8.72	💚
种族: 非西班牙裔白人	2342	7.93	4.38	💚
种族: 非西班牙裔黑人	1525	5.79	3.45	💚
种族: 墨西哥裔美国人	1312	7.77	4.83	💚
家庭收入: $35,000 to $44,999	717	8.34	4.25	💚
家庭收入: $100,000 and over	1182	8.34	5.54	💚

上表比较了微调模型在校正前后的子群体偏倚（NHANES数据集）。绿色（💚）表示偏倚下降，红色（💔）表示偏倚上升。

数据分配策略：这是本文的核心贡献之一。在一个固定1000个可用人类样本的实验中，研究者探索了在微调（FT-History）和校正（$\text{Rec}_{\lambda_{\text{opt}}}$）之间分配这些样本的不同比例所带来的影响。

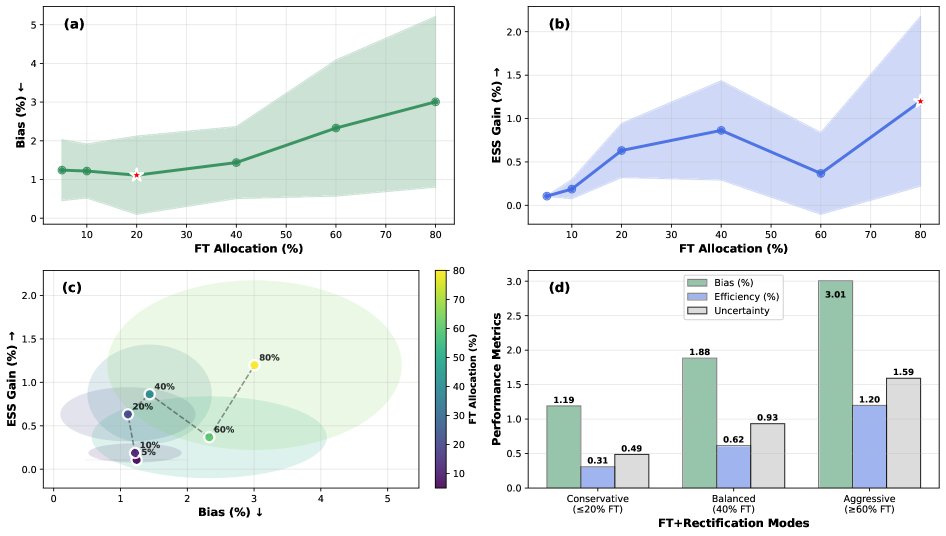数据分配策略图上图展示了不同数据分配比例下的偏倚-效率权衡关系：(a) 将20%数据用于微调、80%用于校正时，偏倚最小；(b) 将更多数据（40-80%）用于微调能获得更高的效率增益，但偏倚和不确定性也随之增加；(c,d) 最佳策略位于帕累托前沿的左上角，被称为“保守”策略（≤20%数据用于微调），它提供了最佳的偏倚-效率平衡。

最终结论

单纯使用LLM进行调查模拟是不可靠的，其输出存在巨大且不稳定的偏倚。
“合成-校正”框架非常有效。它能将偏倚降低到可接受的水平（<5%），同时显著提高估计的统计效率（等同于增加样本量）。
人类数据的最佳用途是校正，而非微调。在资源有限时，应将绝大部分人类数据保留用于校正步骤，仅用一小部分数据进行微调。例如，一个“20%微调，80%校正”的分配策略被证明是平衡偏倚和效率的最佳选择。