What is the objective of reasoning with reinforcement learning?

• ArXiv URL: http://arxiv.org/abs/2510.13651v1

• 作者: Damek Davis; Benjamin Recht

• 发布机构: University of California, Berkeley; University of Pennsylvania

---

TL;DR

本文通过一个统一的数学框架证明，多种用于大型语言模型的流行强化学习算法（如REINFORCE、拒绝采样和GRPO），在处理二元奖励时，都可以被看作是在给定提示下获得正确答案概率的某个单调变换函数上的随机梯度上升，从而揭示了这些算法内在的深刻关联。

关键定义

本文提出了一个统一的分析框架，其核心定义如下：

• 统一目标函数 (Unified Objective Function) $J_h(\theta)$: 本文的核心理论构造，定义为 $J_{h}(\theta):=\mathbb{E}_{x\sim Q}\left[h\left(\sum_{y\in C(x)}\pi_{\theta}(y\mid x)\right)\right]$。该函数旨在最大化一个单调递增函数 $h$ 应用于模型答对问题概率的期望值。不同算法的差异可以归结为选择了不同的变换函数 $h$。

• 正确回答的概率 (Probability of Correctness) $p_{\theta}(C \mid x)$: 定义为 $p_{\theta}(C \mid x):=\sum_{y\in C(x)}\pi_{\theta}(y\mid x)$。它表示在给定提示 (prompt) $x$ 的情况下，从模型 $\pi_{\theta}$ 采样一个回答 $y$，该回答被判定为正确（属于正确答案集合 $C(x)$）的总概率。

• 样本权重 (Per-sample Weight) $Z_i$: 在强化学习文献中通常被称为“优势 (advantages)”。它是在模型参数更新时，应用于每个样本对数概率梯度的权重。更新规则为：$\theta\leftarrow\theta+\eta\frac{1}{M}\sum_{i=1}^{M}Z_{i}\nabla_{\theta}\log\pi_{\theta}(y_{i}\mid x)$。本文的核心洞察在于，权重 $Z_i$ 的不同设计，直接决定了其所优化的统一目标函数中的单调变换 $h$。

相关工作

目前，在大型语言模型（Large Language Models, LLMs）的后训练（post-training）阶段，研究人员广泛使用各种强化学习算法来使模型与人类偏好对齐或提升其在特定测试任务上的能力。这些算法通常遵循一个元算法（Meta-Algorithm）：从语料库中采样提示，让模型生成多个回答，然后由外部评估源（如人工标注或自动验证器）将回答标记为“好”或“坏”，最后根据这些三元组（提示、回答、标签）对模型进行微调。

然而，这一领域存在一个关键问题：尽管如 REINFORCE、拒绝采样微调、GRPO 等算法都遵循上述模式，但它们的具体实现和理论动机各不相同，使得人们不清楚它们各自到底在优化什么具体的目标函数。这种缺乏统一视角的情况，阻碍了对不同算法内在联系的理解和直接比较。

本文旨在解决这一问题，通过提供一个统一的数学框架，证明这些看似不同的算法实际上是在优化一族非常相似的目标函数，从而清晰地揭示了它们之间的关系。

本文方法

统一框架：基于加权的随机梯度上升

本文首先将现有的大多数针对LLM推理的RL微调算法归纳为一个更具体的算法框架（Algorithm 1）：

1. 从语料库 $Q$ 中选择一个问题 $x$。
2. 用当前模型为 $x$ 采样 $M$ 个回答 $y_1, \dots, y_M$。
3. 根据每个回答 $y_i$ 的评估结果（正确或错误），计算一个逐样本的权重 $Z_i$。
4. 使用加权的监督学习更新规则来微调模型：

\[\theta\leftarrow\theta+\eta\frac{1}{M}\sum_{i=1}^{M}Z_{i}\nabla_{\theta}\log\pi_{\theta}(y_{i}\mid x)\]

创新点：从权重到目标函数

本文的核心创新在于揭示了上述更新步骤与优化一个特定目标函数之间的直接联系。作者证明，这个随机梯度更新的期望值恰好是某个目标函数 $J_h(\theta)$ 的梯度。具体来说，不同的权重 $Z_i$ 选择，会导出不同的单调变换函数 $h$，使得：

\[\mathbb{E}_{y_{1:M}}\left[\frac{1}{M}\sum_{i=1}^{M}Z_{i}\nabla_{\theta}\log\pi_{\theta}(y_{i}\mid x)\right]:=\nabla_{\theta}h_{M}(p_{\theta}(C\mid x))\]

这意味着，特定算法所采用的优势函数（即权重 $Z_i$）选择，最终决定了其优化的目标函数 $J_h$ 的形式。通过这个框架，可以分析和比较现有算法的真实优化目标。

权重形式与目标函数的推导

本文考虑了一类特定的权重形式，其值依赖于当前样本是否正确 ($R_i = 1_{y_i \in C(x)}$) 以及其他 $M-1$ 个样本中正确回答的数量 ($S_i = \sum_{j \neq i} R_j$)：

\[Z_{i}=(1-R_{i})a_{S_{i}}+R_{i}b_{S_{i}}\]

其中 $a_s$ 和 $b_s$ 是关于 $s$ 的任意函数。

本文证明，采用此类权重的算法，其诱导出的目标函数变换 $h_M(t)$ 为：

\[h_{M}(t)=\frac{1}{M}\sum_{s=0}^{M-1}(b_{s}-a_{s})I_{t}(s+1,M-s)\]

其中 $I_t(\cdot,\cdot)$ 是正则化不完全贝塔函数。这个通用公式构成了分析具体算法的基础。

具体算法分析

“原始”REINFORCE算法

• 权重选择: $Z_i = 1_{y_i \in C(x)}$，即当回答正确时权重为1，错误时为0。
• 等价目标函数: 这种选择对应于最简单的变换 $h(t) = t$。因此，“原始”REINFORCE算法的目标是直接最大化模型答对问题的平均概率 $\mathbb{E}_{x \sim Q}[p_{\theta}(C \mid x)]$。

拒绝采样 (Rejection Sampling)

• 权重选择: 在一种实现中，从 $M$ 个样本中选出所有正确回答 $V$，并使用梯度估计器 $\frac{1}{ \mid V \mid }\sum_{y\in V}\nabla_{\theta}\log\pi_{\theta}(y\mid x)$。这等价于权重 $Z_i = R_i M / \sum_{j} R_j$（当没有正确回答时跳过更新）。
• 等价目标函数: 这种权重诱导的目标函数 $h_M(t)$ 近似于对数函数 $h(t) = \log(t)$。随着采样数 $M$ 的增大，近似程度越高。
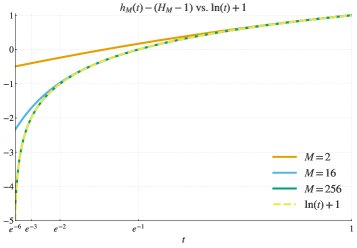
• 纯粹的对数目标: 本文进一步指出，一种“纯粹”的拒绝采样算法（持续采样直到获得 $B$ 个正确回答为止）可以精确地实现对 $J_{\log}(\theta) = \mathbb{E}[\log p_{\theta}(C \mid x)]$ 的随机梯度上升。其梯度估计无偏性可通过对数技巧（log trick）证明：

\[\nabla_{\theta}\log\sum_{y\in C(x)}\pi_{\theta}(y \mid x) = \mathbb{E}[\nabla_{\theta}\log\pi_{\theta}(y \mid x) \mid y\in C(x),x]\]

GRPO 算法

• 权重选择: GRPO算法通过样本奖励的均值和标准差对梯度进行归一化，其权重形式可以表达为：

\[Z_i = \frac{R_{i}-\frac{1}{M}\sum_{j=1}^{M}R_{j}}{\sqrt{\mathrm{Var}(\{R_{j}\}_{j})}+\varepsilon}\]

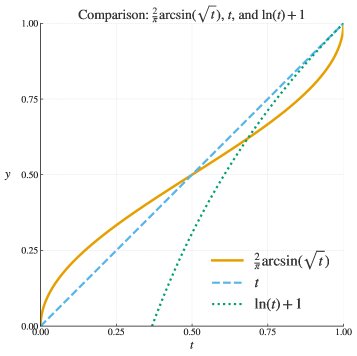
• 等价目标函数: 经过推导，本文表明GRPO所诱导的目标函数 $h_{M, \varepsilon}(t)$ 在理想情况下（$M \to \infty, \varepsilon \to 0$）收敛于反正弦变换 $h(t) = 2\arcsin\sqrt{t}$。理想化的梯度更新可以写作：

\[\nabla_{\theta}h(p_{\theta}(C\mid x)) =\mathbb{E}_{y\sim\pi_{\theta}(y\mid x)}\left[\left(\dfrac{R(y,x)-\mathbb{E}[R(y,x)]}{\sqrt{\mathrm{Var}(R(y,x))}}\right)\nabla_{\theta}\log\pi_{\theta}(y\mid x)\right]\]

下图显示，随着样本量 $M$ 增大和正则化项 $\varepsilon$ 减小，GRPO的实际目标函数（归一化后）趋近于反正弦函数。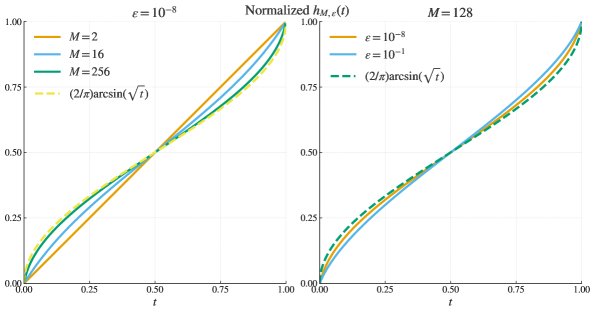

实验结论

本文是一篇理论分析性质的论文，未包含具体的实验部分。其结论是基于数学推导得出的理论洞见：

1. 统一的优化目标: 众多看似不同的RL微调算法，如REINFORCE、拒绝采样和GRPO，实际上都在优化同一个基础目标——最大化正确回答的概率——只不过各自采用了不同的单调函数（如恒等、对数、反正弦）对该概率进行重缩放（rescaling）。

2. 方法选择的类比: 争论哪种算法最优，类似于在监督分类任务中争论逻辑损失（Logistic Loss）与合页损失（Hinge Loss）哪个更好。二者在统计上通常能得到性能相当的分类器，最优选择取决于具体任务和数据。同样，在RL微调中，没有一种缩放函数 $h$ 具有普适的“魔力”，最佳算法将是上下文相关的。

3. 实践启示: 本文的框架为设计新的微调算法提供了“配方”。研究者可以先确定一个期望的缩放函数 $h(t)$（例如，对数几率函数 $h(t)=\log(t/(1-t))$），然后利用本文提出的基于伯恩斯坦多项式的方法反向构造出相应的样本权重 $Z_i$。

最终，本文的结论是，所有这些算法都在追逐紧密相关的目标。由于所有目标函数都是单调的，它们的全局最优点是相同的（即模型对所有问题的正确答案集合赋予100%的概率）。算法之间的差异主要体现在优化动态上，而非最终目标上。这个统一的视角为该领域的研究者提供了更清晰的理解和更大的设计灵活性。