Who Said Neural Networks Aren’t Linear?

• ArXiv URL: http://arxiv.org/abs/2510.08570v1

• 作者: Assaf Hallak; Nimrod Berman; Assaf Shocher

• 发布机构: Ben-Gurion University; NVIDIA; Technion

---

TL;DR

本文提出了一种名为 Linearizer 的新架构，通过将一个线性算子置于两个可逆神经网络之间，使得传统的非线性映射在特定构造的向量空间中表现为严格的线性变换，从而能够将线性代数的强大工具（如SVD、伪逆）应用于深度学习模型。

关键定义

本文的核心是重新定义向量空间，使非线性函数在其上呈线性。关键定义如下：

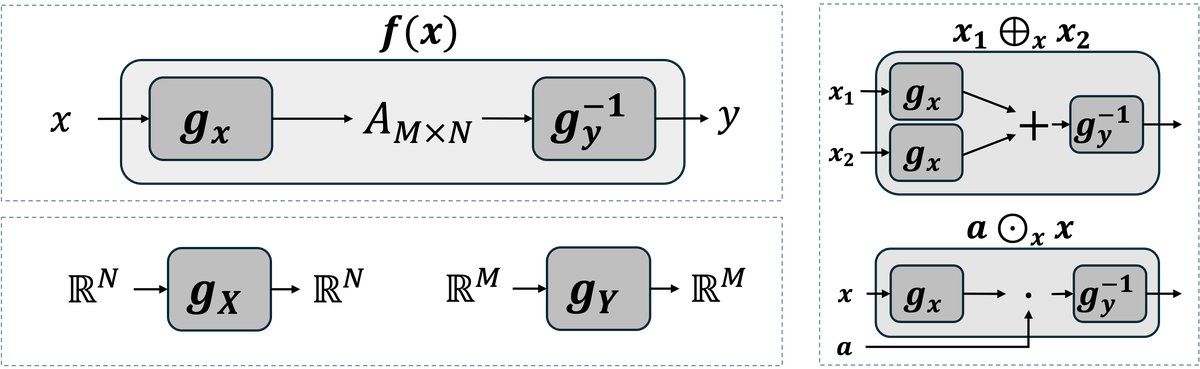
1. Linearizer: 一种复合函数架构，其形式为 $f(x) = \mathbb{L}_{{g_x, g_y, A}}(x) = g_y^{-1}(A g_x(x))$。其中，$g_x$ 和 $g_y$ 是可逆的神经网络，$A$ 是一个线性算子（矩阵）。这个架构在标准欧几里得空间中是非线性的。

2. 诱导向量空间运算 (Induced Vector Space Operations): 基于可逆网络 $g$ 定义的新型向量加法和标量乘法。对于向量 $v_1, v_2$ 和标量 $a$，运算定义为：
   • 向量加法: $v_1 \oplus_g v_2 := g^{-1}(g(v_1) + g(v_2))$
   • 标量乘法: $a \odot_g v_1 := g^{-1}(a \cdot g(v_1))$ 通过这些运算，集合 $\mathbb{R}^N$ 与标量域 $\mathbb{R}$ 构成了一个新的向量空间 $(V, \oplus_g, \odot_g)$。

3. 诱导内积 (Induced Inner Product): 同样基于可逆网络 $g$ 定义的新内积，使得诱导的向量空间成为希尔伯特空间 (Hilbert spaces)。其定义为：

   \[\langle v_1, v_2 \rangle_g := \langle g(v_1), g(v_2) \rangle_{\mathbb{R}^N}\]

   其中，等式右侧为标准欧几里得内积。

相关工作

当前的神经网络模型是著名的非线性模型，这虽然赋予了它们强大的表达能力，但也使其无法利用经典线性代数中丰富而优雅的理论工具。在线性系统中，诸如特征分解、求逆、投影等操作都具有明确的结构和理论保障，而迭代一个线性算子也会使问题简化。但在非线性系统中，这些任务变得异常复杂，通常需要设计专门的损失函数和优化策略，且结果往往是近似的。

本文旨在解决的核心问题是：能否在不牺牲非线性模型表达能力的前提下，重新将其诠释为线性算子？如果可以，那么将能够直接利用线性代数的全部工具来分析和操作这些复杂的非线性模型。

本文方法

架构

本文提出的核心方法是 Linearizer 架构。其结构是将一个线性算子（矩阵 $A$）夹在两个可逆的神经网络 $g_x$ 和 $g_y$ 之间：

\[f(x) = g_y^{-1}(A g_x(x))\]

其中，$g_x$ 将输入数据 $x$ 映射到一个隐空间 (latent space)，$A$ 在此隐空间中进行线性变换，然后 $g_y^{-1}$ 将结果映射回输出空间。

Linearizer 结构（上）是一个线性操作，夹在两个可逆函数之间。（下）向量加法和标量乘法定义了诱导向量空间，在此空间中 f 是线性的。

创新点

Linearizer 的本质创新在于，它证明了函数 $f$ 在由 $g_x$ 和 $g_y$ 诱导出的新向量空间中是严格线性的。具体来说：

1. 构造性线性化：通过定义新的加法 $\oplus$ 和数乘 $\odot$ 运算，本文为输入和输出构造了新的向量空间。输入空间 $\mathcal{X}$ 由 $(\oplus_x, \odot_x)$ 定义（基于 $g_x$），输出空间 $\mathcal{Y}$ 由 $(\oplus_y, \odot_y)$ 定义（基于 $g_y$）。在该框架下，函数 $f$ 满足叠加原理，即被证明是线性的：

   \[f(a_1 \odot_x x_1 \oplus_x a_2 \odot_x x_2) = a_1 \odot_y f(x_1) \oplus_y a_2 \odot_y f(x_2)\]

2. 几何直觉: 可逆映射 $g_x$ 可以看作是一种微分同胚 (diffeomorphism)，它将数据空间中的弯曲流形“拉直”为隐空间中的平坦空间。因此，在数据空间看来复杂的变换路径，在隐空间中只是简单的直线。

优点

这种线性化的构造赋予了模型一系列强大的代数性质，这些性质可以直接通过操作核心矩阵 $A$ 来实现：

• 复合 (Composition): 两个共享中间可逆网络 $g_y$ 的 Linearizer 的复合仍然是一个 Linearizer，其核心矩阵是两个原始矩阵的乘积 $A_2 A_1$。

• 迭代 (Iteration): 当 $g_x = g_y = g$ 时，对函数 $f$ 进行 N 次迭代等价于对矩阵 $A$ 进行 N 次幂乘：

  \[f^{\circ N}(x) = g^{-1}(A^N g(x))\]

• 转置 (Transpose): 函数 $f$ 的转置 $f^\top$ 也是一个 Linearizer，其核心矩阵是 $A^\top$：

  \[f^\top(y) = g_x^{-1}(A^\top g_y(y))\]

• 伪逆 (Pseudo-inverse): 函数 $f$ 的摩尔-彭若斯伪逆 $f^\dagger$ 同样是一个 Linearizer，核心矩阵是 $A$ 的伪逆 $A^\dagger$：

  \[f^\dagger(y) = g_x^{-1}(A^\dagger g_y(y))\]
• 奇异值分解 (SVD): 整个非线性函数 $f$ 的 SVD 可以通过对核心矩阵 $A$ 进行 SVD 来构造。

实验结论

本文通过三个应用展示了 Linearizer 框架的实际效用。

一步流匹配 (One-Step Flow Matching)

• 方法: 传统的流匹配（扩散）模型需要通过多步迭代积分来从噪声生成数据，过程缓慢。本文将流匹配模型构建为 Linearizer 架构。在诱导的线性空间中，多步欧拉积分 $\prod_{i=0}^{N-1}(I+\Delta t\,A_{t_i})$ 可以被坍缩 (collapse)为一个单一的矩阵 $B$。因此，生成过程从一个多步迭代过程简化为一次前向传播：

  \[\hat{x}_1 = g^{-1}(B g(x_0))\]

• 结论:

  • 一步生成: 在 MNIST 和 CelebA 数据集上，该方法实现了高质量的单步生成，其输出与 100 步迭代生成的结果在视觉上无法区分（MSE 为 $3.0 \times 10^{-4}$）。
  • 性能验证: 单步生成的 FID 分数与 100 步迭代的结果相当，验证了理论的正确性。
  • 精确反演: 利用 $f^\dagger$ 的性质，模型可以实现精确的编码器功能，将真实图像映射回隐空间，这是标准扩散模型难以做到的。这使得图像重建和插值成为可能。

左右两侧（红色）为原始（非生成）数据 $x\_1$ 和 $x\_2$。中间图像是通过在隐空间插值获得的。

量化比较结果

数据集	反演重建一致性 (LPIPS)	100步 vs 1步保真度 (LPIPS)
MNIST	31.6 / .008	32.4 / .006
CelebA	33.4 / .006	32.9 / .007

注：表格中的两个数值分别代表LPIPS和PSNR。LPIPS越低越好。

模块化风格迁移

• 方法: 将不同的艺术风格与不同的核心矩阵 $A_{\text{style}}$ 关联起来，而内容信息由共享的 $g_x$ 提取。风格迁移函数为 $f_{\text{style}}(x) = g_y^{-1}(A_{\text{style}} g_x(x))$。
• 结论: 这种架构将内容和风格完全分离。不同风格可以像代数对象一样被轻松组合，例如，通过对两个风格矩阵进行线性插值 $\alpha A_1 + (1-\alpha) A_2$，可以实现两种风格之间的平滑过渡。

左：原图。中：使用左右风格图进行风格迁移。右：两种风格之间的插值。

线性幂等生成网络

• 方法: 幂等性 ($f(f(x)) = f(x)$) 在代数和机器学习中都非常重要。在 Linearizer 框架中，要使 $f$ 成为幂等函数，只需保证其核心矩阵 $A$ 是幂等的 ($A^2=A$)，即一个投影矩阵。本文通过架构设计（使用直通估计器 Straight-Through Estimator）直接构造了一个可微的投影矩阵，从而构建了一个天然幂等的生成模型。
• 结论:
  • 全局投影仪: 与以往仅在训练数据附近近似实现幂等性的方法（如 IGNs）不同，本文模型由于其架构保证，是一个全局投影仪。它可以将任意输入都投影到目标数据流形上。
  • 无需噪声注入: 模型在训练期间不注入噪声，整个环境空间都可作为输入源，这是一种非常独特的生成模型。

黑色实线箭头表示前向传播；红色虚线箭头表示反向传播。我们的线性IGN构建了一个全局投影仪，可将任何输入投影到目标分布。上方是输入，下方是匹配的输出。