Why Low-Precision Transformer Training Fails: An Analysis on Flash Attention

TL;DR

本文首次系统性地揭示了在使用Flash Attention进行低精度（BF16）Transformer模型训练时，导致训练崩溃的内在机制，指出其根源在于注意力机制中出现的相似低秩表示与BF16算术固有有偏舍入误差的累积效应，两者共同形成恶性循环，最终导致损失爆炸。

关键定义

本文主要沿用现有概念，并对以下对理解本文至关重要的术语进行了深入分析：

  1. bfloat16 (BF16)：一种16位浮点数格式，包含1个符号位、8个指数位和7个有效数字位。它的动态范围与32位单精度（FP32）相同，但精度更低。本文的关键在于揭示了在特定数据分布下，BF16的舍入操作（通常是“四舍五入到最近的偶数”）会产生 有偏舍入误差 (biased rounding error)，即误差会持续向单一方向累积，而非随机抵消。

  2. Flash Attention (FA)：一种I/O感知的精确注意力算法，通过分块计算（tiling）将注意力机制的内存复杂度从关于序列长度 $N$ 的 $O(N^2)$ 降低到 $O(N)$。本文的分析聚焦于FA反向传播中的一个关键中间项 \(δ\)，其计算方式为 \(δ = rowsum(dO ◦ O)\)，并发现该计算在BF16精度下是数值不稳定的主要来源。

相关工作

当前，训练更大规模的Transformer模型依赖于低精度计算（如BF16、FP8）来提升效率。Flash Attention因其能高效处理长序列而成为训练大模型的基石。然而，一个长期存在且未被解决的瓶颈是，在低精度（特别是BF16）设置下使用Flash Attention时，训练过程常常会因灾难性的损失爆炸而突然失败。

尽管社区提出了一些经验性的修复方法，如QK归一化（QK normalization）、QK裁剪（QK-clip）和门控注意力（Gated Attention），但这些方法更像是“创可贴”，未能从根本上解释失败的原因。研究现状缺乏一个从数值误差到训练崩溃的清晰因果链条。

本文旨在解决这一具体问题：为BF16精度下Flash Attention训练失败的现象提供首个机理层面的解释，并基于此提出 principled 的解决方案，而非依赖临时的经验性修复。

本文方法

本文的核心“方法”并非提出一个全新的模型，而是一套严谨的逆向分析（reverse-engineering）流程，通过层层剥茧，最终定位并验证了低精度训练失败的根本原因。

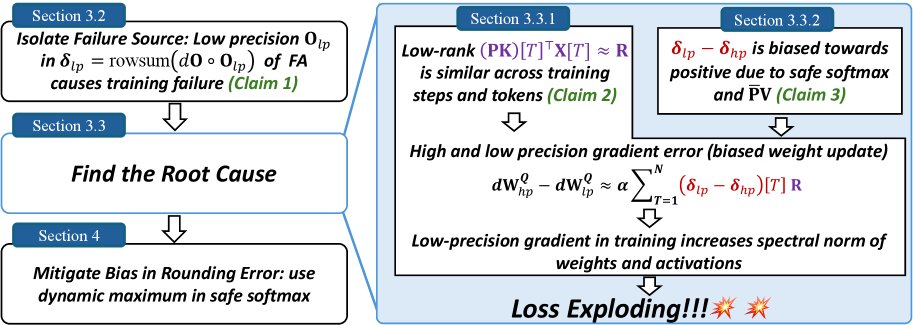
分析流程图

本文通过逆向追踪训练失败的因果链（蓝色框）来识别根本原因。

复现与定位失败源头

首先，本文在一个GPT-2模型上稳定复现了社区报告的训练失败现象：在使用BF16和Flash Attention训练数千步后，损失突然爆炸。为保证分析的确定性，本文使用了固定的数据批次顺序。

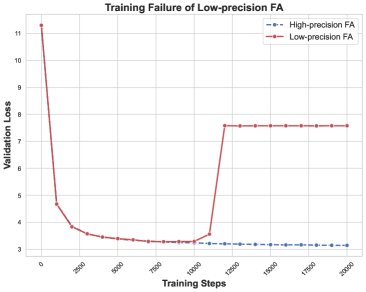
训练失败现象

使用BF16和Flash Attention的配置（不稳定）出现损失爆炸，而稳定配置正常收敛。

通过一系列隔离实验，本文逐步缩小了问题范围：

  1. 排除分块计算：即使禁用Flash Attention的分块（tiling）策略，问题依旧存在，表明失败与分块无关。
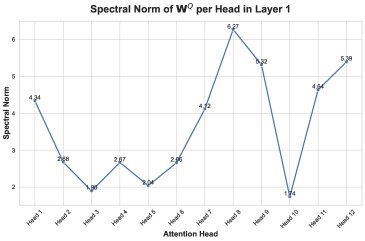
  2. 定位到特定层和模块：通过监测各层权重矩阵的谱范数，发现异常主要集中在第2层的注意力模块。仅在该层使用Flash Attention足以复现失败，而仅在该层换用标准注意力则能稳定训练。
  3. 锁定关键计算步骤：在Flash Attention的反向传播中，一个关键中间项 \(δ\) 的计算被确定为问题所在。\(δ\) 的标准计算为 \(δ = rowsum(dO ◦ O)\)。实验发现，若换用一个数学上等价但在数值上更稳定的计算方式，或在计算 \(δ\) 时将前向传播得到的输出 \(O\) 临时用FP32精度重算，训练就能恢复稳定。这有力地证明了 BF16精度下计算得到的输出矩阵 \(O\) 的数值误差是失败的直接原因。
  4. 细化到特定注意力头：进一步分析发现，失败主要由少数几个注意力头（特别是第8个头）的谱范数异常增长引起。后续分析便聚焦于这个最不稳定的头。

特定注意力头的谱范数异常

第2层注意力模块中，第8个头的查询权重矩阵 $$W^Q$$ 谱范数最大，成为分析焦点。

揭示根本原因：两大因素的恶性循环

本文的分析揭示了训练失败是由两个相互关联的因素共同作用导致的恶性循环。

原因一：相似低秩矩阵与有偏系数导致权重更新偏差

梯度误差的来源被追溯到查询权重矩阵 \(W^Q\) 的梯度差异 \(dW^Q_hp - dW^Q_lp\)。该差异可表示为：

\[d{\mathbf{W}}^{Q}_{hp}-d{\mathbf{W}}^{Q}_{lp} = \alpha\sum_{T=1}^{N}({\mathbf{\delta}}_{lp}-{\mathbf{\delta}}_{hp})[T]\cdot({\mathbf{P}}{\mathbf{K}})[T]^{\top}{\mathbf{X}}[T]\]

其中，\(δ_lp - δ_hp\) 是低精度和高精度计算下 \(δ\) 向量的差异，\(P\) 是注意力概率矩阵，\(K\) 是键矩阵，\(X\) 是输入特征。这个公式表明，总的梯度误差是N个秩-1矩阵的加权和，权重为 \(δ\) 的误差项。

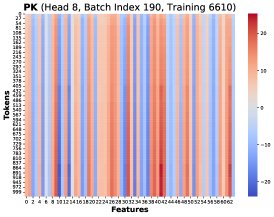
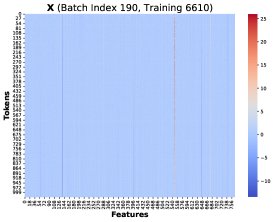
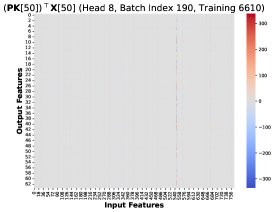
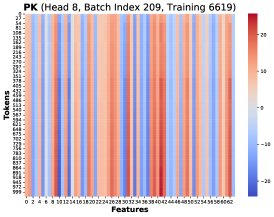
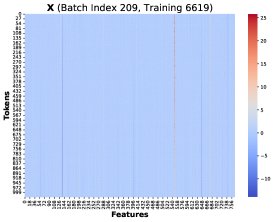
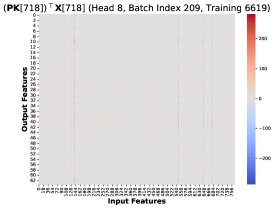
相似的低秩结构 相似的低秩结构 相似的低秩结构 相似的低秩结构 相似的低秩结构 相似的低秩结构

在不同训练步和Token位置，矩阵 $$(PK)[T]^T X[T]$$ 呈现出高度相似的结构。

核心发现1：本文通过可视化发现，在不同训练步和不同Token位置 \(T\)，这些秩-1矩阵 \((PK)[T]^T X[T]\) 存在高度相似的结构。因此，总梯度误差可以近似为一个共同的低秩结构 \(R\) 乘以一个标量系数：

\[d{\mathbf{W}}^{Q}_{hp}-d{\mathbf{W}}^{Q}_{lp} \approx \alpha\left(\sum_{T=1}^{N}({\mathbf{\delta}}_{lp}-{\mathbf{\delta}}_{hp})[T]\right) {\mathbf{R}}\]

核心发现2：对系数 \(Σ(δ_lp - δ_hp)[T]\) 的累积和进行追踪，发现它在训练崩溃前持续为正，表现出明显的正向偏置。

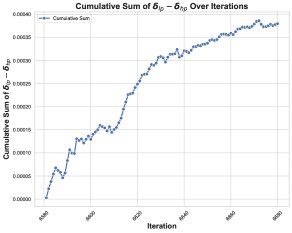
系数的正向偏置

在训练失败前，误差系数 $$(δ_lp - δ_hp)[T]$$ 的和持续为正，导致误差不断累积。

这两个发现共同揭示了失败的第一环：由于系数持续为正，相似的低秩误差 \(R\) 在多个训练步中不断累积，而不是随机抵消。这种累积性的误差污染了权重更新，导致权重的谱范数和激活值异常增大，最终使训练动态崩溃。

原因二：有偏舍入误差导致系数 \((δ_lp - δ_hp)[T]\) 为正

接下来，本文探究了为何系数 \((δ_lp - δ_hp)[T]\) 会持续为正。 \(δ\) 的误差 \(δ_lp - δ_hp\) 主要来源于 \(dO\) 与 \(O_lp - O_hp\) 的逐元素乘积。分析显示，在某些关键的特征维度上，\(dO\) 的值和 \(O\) 的计算误差 \(O_lp - O_hp\) 倾向于同为负值，导致它们的乘积为正，从而贡献了正的 \(δ\) 误差。

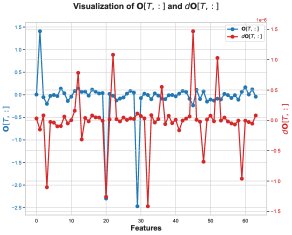
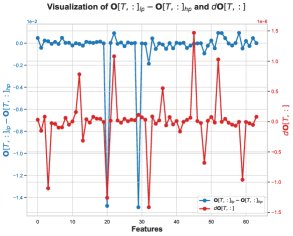
误差来源分析 误差来源分析

在特征维度20和29，$$dO$$（b图）和 $$O$$ 的误差 $$O_lp - O_hp$$（c图）均呈现显著的负值，其乘积为正，导致 $$δ$$ 误差为正。

\(O\) 的误差 \(O_lp - O_hp\) 为负，意味着BF16计算的输出 \(O_lp\) 系统性地偏向比FP32结果 \(O_hp\) 更负的值。这一偏置被追溯到 \(O\) 计算过程中的一个中间步骤：未归一化的输出 \(Ō = P̄V\) 的矩阵乘法。

核心发现3：在这个矩阵乘法中，数值误差主要发生在注意力概率 \(P̄[T, t]\) 恰好为1的那些位置。这通常发生在softmax之前的某个分数是该行最大值时。当 \(P̄[T, t] = 1\) 时，\(P̄V\) 的计算就简化为对\(V\)矩阵某些行的累加。

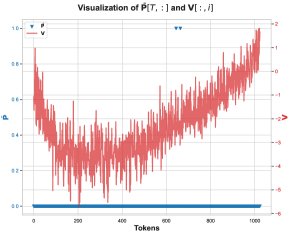
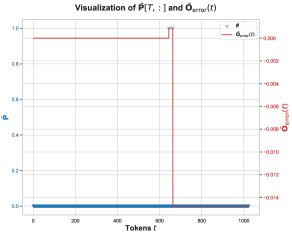
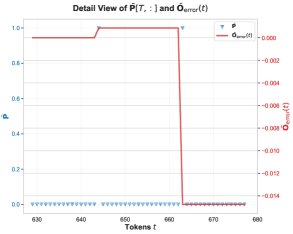
有偏舍入误差的成因 有偏舍入误差的成因 有偏舍入误差的成因

(a) $$V$$ 矩阵在问题维度（如20）的值大多为负。(b, c) 当 $$P̄[T,t]=1$$ 时，累加负的 $$V$$ 值导致 $$Ō$$ 的计算误差显著地向负方向跳变。

核心发现4：在出现问题的特征维度上，\(V\) 矩阵的值绝大多数为负。因此，当累加这些 predominantly negative 的BF16数值时，BF16的舍入机制会产生有偏的舍入误差，使得累加和的结果系统性地比真实值更负。这就解释了 \(O_lp\) 为何会偏向更负的值。

解决方法

基于上述分析，本文提出了一个极简的修复方案：在Flash Attention的实现中，通过微小的修改来缓解计算 \(Ō = P̄V\) 过程中的有偏舍入误差。论文虽然没有详述修改的具体代码，但暗示这可能通过改变累加顺序、或在关键累加步骤中使用更高精度来实现。这个简单的改动成功稳定了原本会失败的训练过程。

实验结论

本文的实验结论主要通过其分析和验证过程体现：

本文的分析不仅解释了问题，其提出的修复方案也为实现更稳健、更高效的低精度大模型训练提供了重要的实践指导。