Zero-Shot Performance Prediction for Probabilistic Scaling Laws
-
ArXiv URL: http://arxiv.org/abs/2510.16743v1
-
作者: Daniel Beck; Trevor Cohn; Markus Hiller
-
发布机构: Google; Royal Melbourne Institute of Technology; The University of Melbourne
TL;DR
本文提出一种新框架,通过将学习曲线(learning curves, LCs)预测问题建模为具有双层层级结构的多任务学习问题,并利用潜变量多输出高斯过程来捕捉任务间的相关性,从而实现对模型性能学习曲线的零样本(zero-shot)预测,进而以更低的计算成本生成概率性的缩放定律(scaling laws)。
关键定义
- 双层层级结构 (Bi-level Hierarchy):本文的核心观点,指自然语言处理(NLP)领域的学习曲线数据集内部存在一种层级关系。例如,在模型缩放实验中,可以将嵌入维度作为第一层级(任务),将网络层数作为第二层级(任务内的数据实例),以此来组织和建模不同模型配置下的性能数据。
- 潜变量多输出高斯过程 (Latent Variable Multi-output Gaussian Process, Ma):本文采用的核心模型。它是一种高斯过程的扩展,通过引入共享的均值函数和任务特定的潜变量,能够同时对多个相关联的输出(即多条学习曲线)进行建模,并有效捕捉它们之间的共享信息与相关性。
- 概率性缩放定律 (Probabilistic Scaling Laws):非传统的、单一的缩放定律曲线,而是通过蒙特卡洛模拟从模型的后验预测分布中生成的一组缩放定律。这种方法不仅给出了性能预测的期望值,还量化了预测的不确定性,形成一个“定律的分布”。
- 学习曲线的零样本预测 (Zero-Shot Prediction of Learning Curves):在未见过任何目标模型配置(如一个全新的模型尺寸)的性能数据的情况下,仅根据在其他相关模型配置上训练得到的知识,直接预测出目标模型的完整学习曲线。
相关工作
现有研究领域中,学习曲线预测早期依赖于参数化函数(如幂律、指数函数)进行外推。后续在贝叶斯优化等领域,开始采用高斯过程(Gaussian Processes, GPs)、贝叶斯神经网络(Bayesian Neural Networks, BNNs)等代理模型。而缩放定律的推导通常依赖于大规模、高成本的经验性研究,即训练大量不同配置的模型来收集数据,这种方法资源消耗巨大。
本文旨在解决的核心问题是:如何显著降低推导缩放定律所需的巨大计算成本。传统方法需要详尽地训练所有模型,而本文试图通过预测未见过的、尤其是更大、更昂贵的模型的学习曲线,来规避这一高昂的训练开销。
本文方法
创新点
本文的本质创新在于提出了一种新的视角和建模框架,而非发明一种全新的算法。其核心思想是,将一系列相关的学习曲线数据集(如不同尺寸模型的性能曲线)视为一个具有内在层级结构的多任务问题。
例如,对于一系列由不同嵌入维度和网络层数构成的语言模型,可以将“嵌入维度”视为顶层任务(task),而将相同嵌入维度下的不同“网络层数”视为该任务下的子实例(data instances)。这种层级结构(如图1所示)揭示了模型家族内部的关联性。
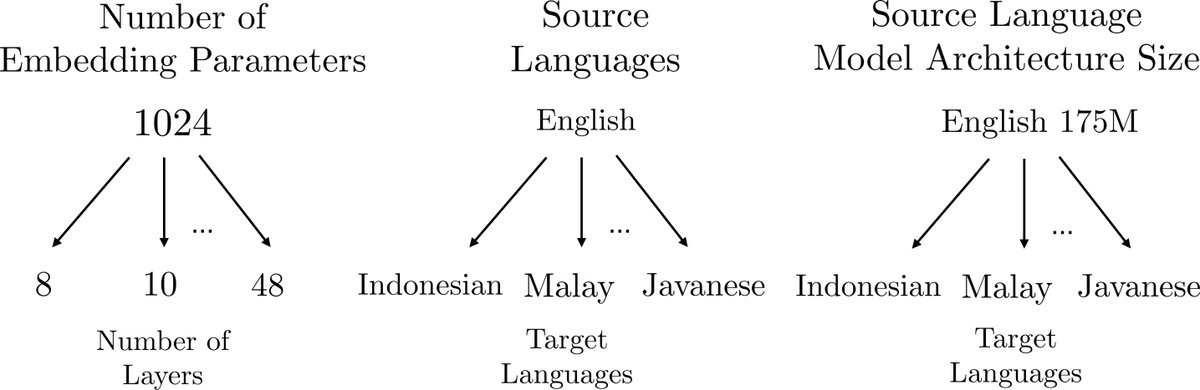
优点
该方法的主要优点是数据效率和知识迁移能力。通过显式地为数据建立层级结构,并使用能够捕捉任务间相关性的模型,可以实现“举一反三”:
- 信息共享:模型可以从已知的、较小模型的学习曲线中学到通用的性能变化规律。
- 关联建模:模型能够利用不同任务(如不同嵌入维度)之间的相似性。
- 零样本预测:综合以上两点,模型有能力对完全未见过的模型配置(特别是更大、计算成本更高的模型)进行性能预测,从而避免了实际训练这些模型的巨大开销。
模型与流程
1. 模型选择:潜变量多输出高斯过程 (Ma)
为了实现上述构想,本文采用了Alvarez等人提出的潜变量多输出高斯过程(Ma)模型。其生成过程如下:
\[\begin{align*} g(\mathbf{x}) &\sim \mathcal{GP}(0, k_g(\mathbf{x}, \mathbf{x}')) \\ l_t^d(\mathbf{x}) &\sim \mathcal{GP}(g(\mathbf{x}), k_l(\mathbf{x}, \mathbf{x}')) \\ y_t^d(\mathbf{x}) &= l_t^d(\mathbf{x}, \mathbf{h}_t) + \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, \sigma^2), \quad \mathbf{h}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{align*}\]- $y_t^d(\mathbf{x})$ 是观测到的带噪声的学习曲线上的点,其中 $t$ 索引任务(如嵌入维度),$d$ 索引任务内的数据实例(如层数),$\mathbf{x}$ 是输入(如计算量或数据集大小)。
- $l_t^d(\mathbf{x})$ 是真实的学习曲线,它从一个高斯过程中抽取。
- $g(\mathbf{x})$ 是一个所有任务共享的均值函数(先验),代表了所有学习曲线共同的趋势。
- $\mathbf{h}_t$ 是一个任务相关的潜变量,用于捕捉不同任务(不同层级)之间的相关性。 通过这个模型,对新任务(未见过的模型配置)的预测 $l^*$ 服从一个高斯分布 $q(\mathbf{l}^* \mid \mathbf{X}^*)$,其均值和协方差给出了预测曲线的期望和不确定性。
2. 方法流程:生成概率性缩放定律
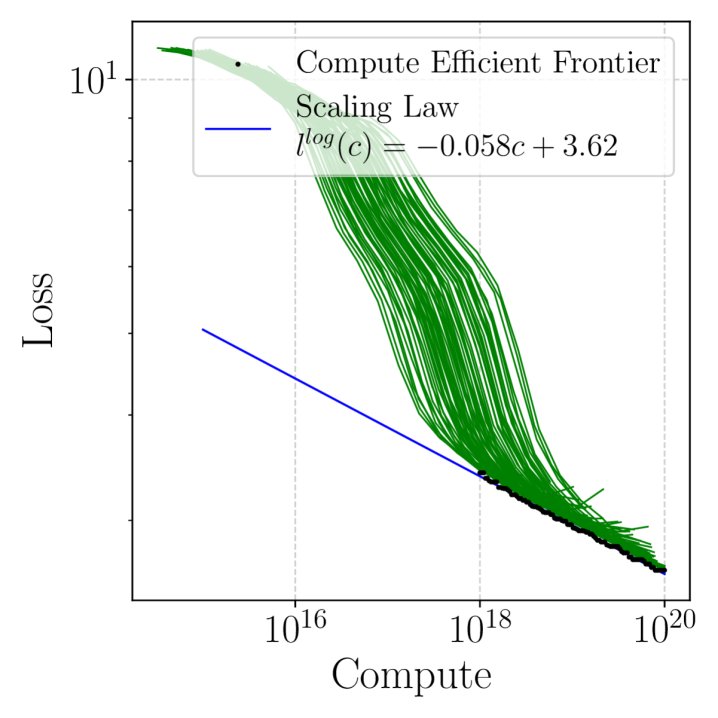
本文提出的生成概率性缩放定律的流程如下:
- 训练:在一个已知的学习曲线子集 $\mathcal{D}$ 上训练Ma模型。
- 零样本预测:使用训练好的模型,预测出缺失的、未知的学习曲线集合 $\mathcal{D}^*$。这个预测结果是一个后验分布,包含了不确定性。
- 蒙特卡洛模拟:进行 $R$ 次模拟。在每次模拟 $r$ 中: a. 从后验分布中为 $\mathcal{D}^*$ 采样一组具体的学习曲线。 b. 将采样的曲线与已知曲线 $\mathcal{D}$ 合并。 c. 在合并后的数据集上,找到计算高效边界(compute-efficient frontier),并拟合一个缩放定律,如 $l(c) = (c/c_0)^{-\gamma}$。在log-log空间中,这对应于线性拟合 $l^{\log}(c) \sim \mathcal{N}(\beta_0 + \beta_1 c, \sigma^2)$。
- 汇总:将 $R$ 次模拟得到的缩放定律参数(如 $\beta_0, \beta_1$)进行平均,得到最终的概率性缩放定律的期望值和方差。
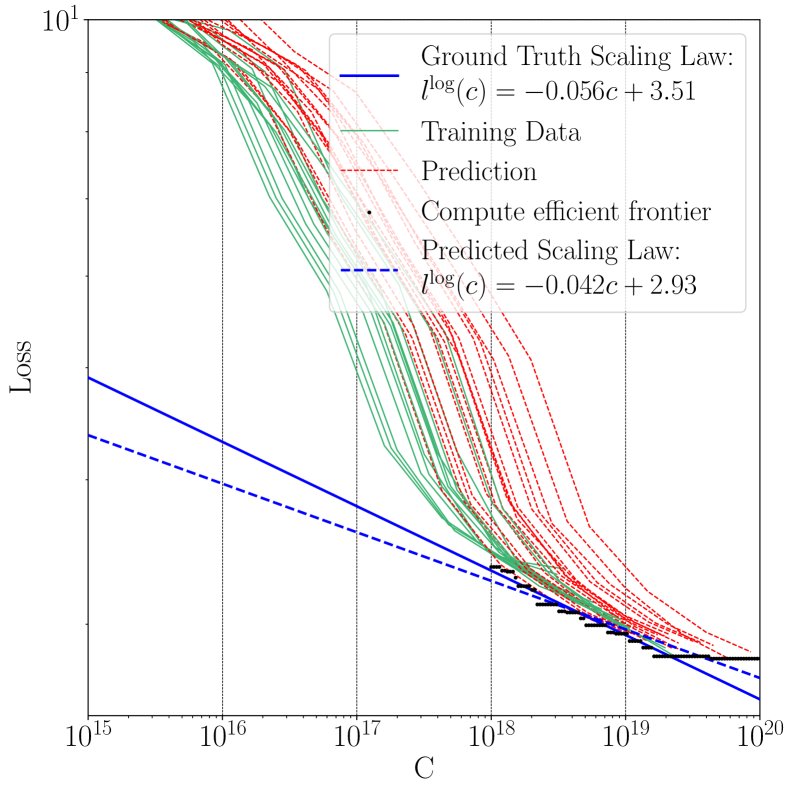
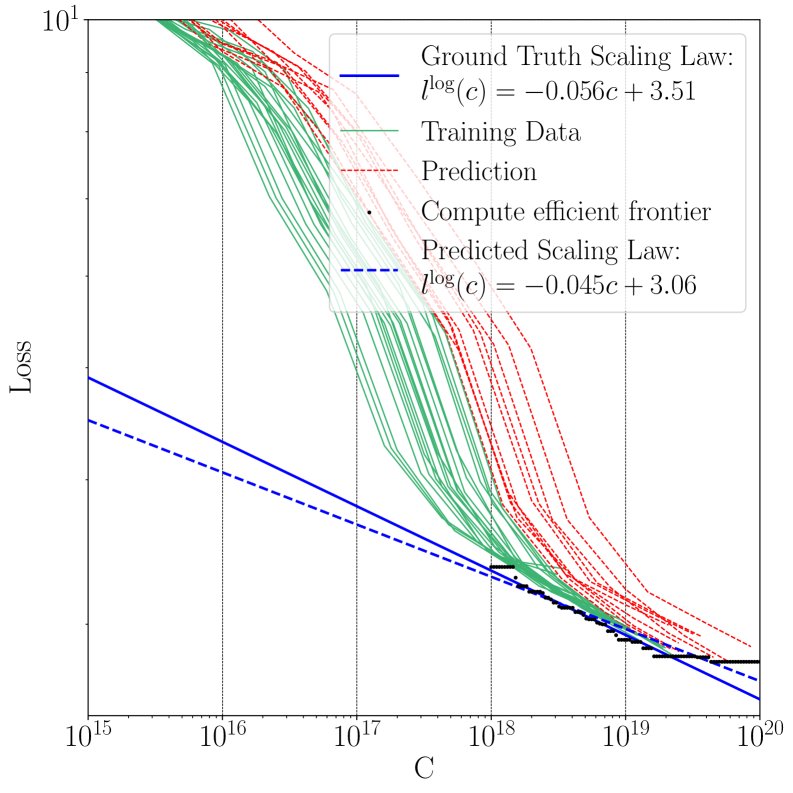
数据集层级定义
本文在多个NLP数据集上验证了该框架的普适性,并为它们定义了层级结构:
- nanoGPT (缩放定律): 任务 $t$ 对应嵌入维度,实例 $d$ 对应网络层数。
- 双语翻译 (mBART/Transformer): 任务 $t$ 对应源语言,实例 $d$ 对应目标语言。
- 多语种翻译 (M2M100): 任务 $t$ 对应源-目标语言对,实例 $d$ 对应不同的模型尺寸。

实验结论
零样本预测性能
实验在nanoGPT数据集上进行,与BNN(贝叶斯神经网络)等基线模型进行比较。
核心结论:
- 本文提出的Ma模型在所有评估指标上均显著优于基线模型。如下表所示,其在均方根误差(RMSE)、平均绝对误差(MAE)和负对数预测密度(NLPD)上都取得了最低值(越低越好)。
- 这一结果强有力地支持了核心假设:显式地建模NLP学习曲线数据集中的层级结构和任务相关性,能够有效提升零样本预测的准确性。
- 实验还证实,层级是可交换的(即将嵌入维度和层数在层级定义中互换),Ma模型依然表现出色,证明了框架的鲁棒性。
| 模型 (nanoGPT) | RMSE | MAE | NLPD |
|---|---|---|---|
| Ma (Quad) | 0.021±0.00 | 0.016±0.00 | -2.02±0.01 |
| DHGP (Quad) | 0.026±0.00 | 0.020±0.00 | -1.82±0.00 |
| BNN (LC) (Quad) | 0.038±0.00 | 0.033±0.00 | -1.54±0.01 |
| BNN (orig) (Quad) | 0.041±0.00 | 0.035±0.00 | -1.48±0.01 |
| Ma (Tri) | 0.017±0.00 | 0.013±0.00 | -2.22±0.02 |
| DHGP (Tri) | 0.021±0.00 | 0.016±0.00 | -2.00±0.01 |
| BNN (LC) (Tri) | 0.025±0.00 | 0.021±0.00 | -1.84±0.01 |
| BNN (orig) (Tri) | 0.026±0.00 | 0.022±0.00 | -1.80±0.00 |
| Ma (T1) | 0.032±0.00 | 0.025±0.00 | -1.63±0.01 |
| DHGP (T1) | 0.035±0.00 | 0.028±0.00 | -1.57±0.01 |
概率性缩放定律预测
使用不同训练/测试集划分(Quad, Tri, T1)来预测缩放定律,并与使用全量数据得到的“真实”缩放定律进行比较。
核心结论:
- 该方法能够以少量数据预测出与真实缩放定律非常接近的曲线。
- 使用曲线下面积(Area between Curves, AbC)作为度量,不同数据划分策略在成本和精度之间存在权衡。例如,Quad划分训练成本最低,但AbC误差最高。
| TT Split | $\hat{\beta}_0$ | $\hat{\beta}_1$ | AbC (mean±std) |
|---|---|---|---|
| Ground Truth | |||
| nanoGPT | -1.026 | -0.198 | - |
| nanoGPT (Quad) | -1.332 | -0.170 | - |
| nanoGPT (Tri) | -1.134 | -0.188 | - |
| nanoGPT (T1) | -1.109 | -0.190 | - |
| Predictions | |||
| nanoGPT (Quad) | -1.972±0.51 | -0.141±0.01 | 0.701±0.30 |
| nanoGPT (Tri) | -0.730±1.07 | -0.208±0.02 | 0.603±0.49 |
| nanoGPT (T1) | -0.999±1.33 | -0.193±0.03 | 0.286±0.61 |
主动学习策略
为了进一步提升效率,本文探索了主动学习(active learning)策略,即如何智能地选择下一个要“查询”(即实际训练并获取其LC)的模型,以最快地降低缩放定律的预测不确定性。
核心结论:
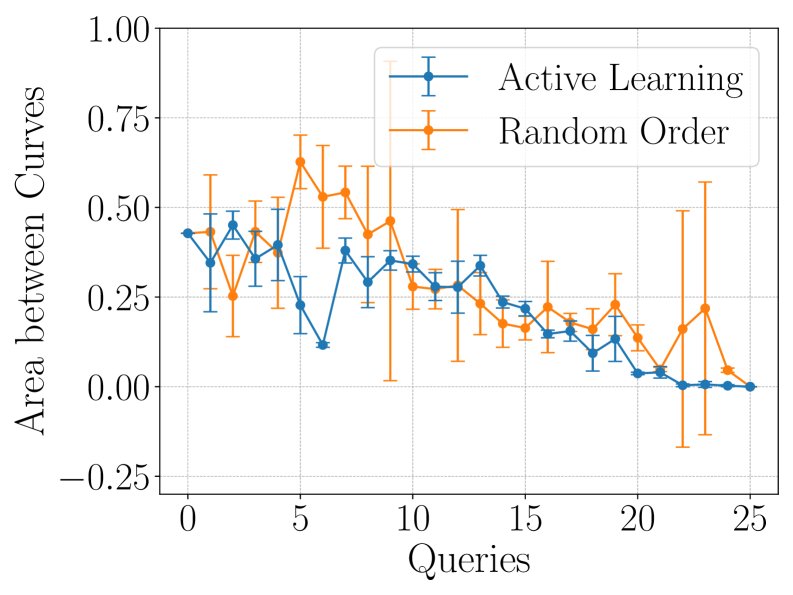
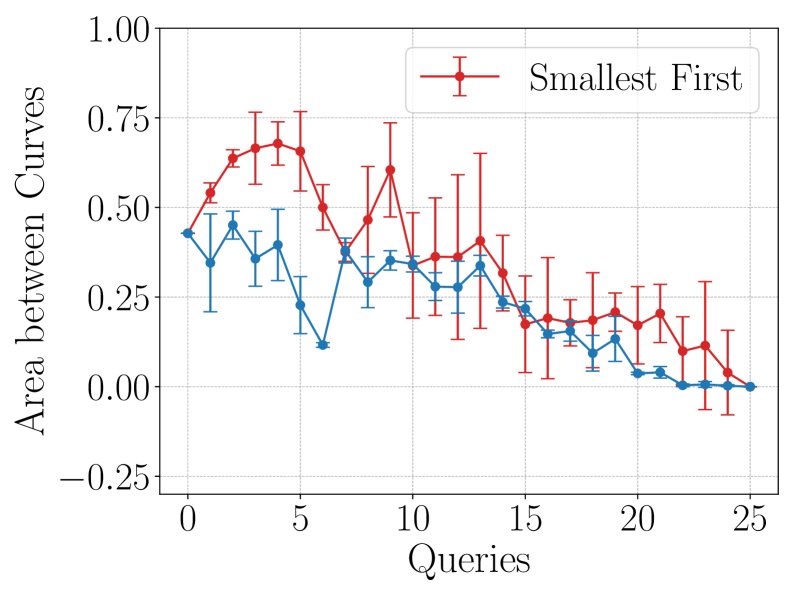
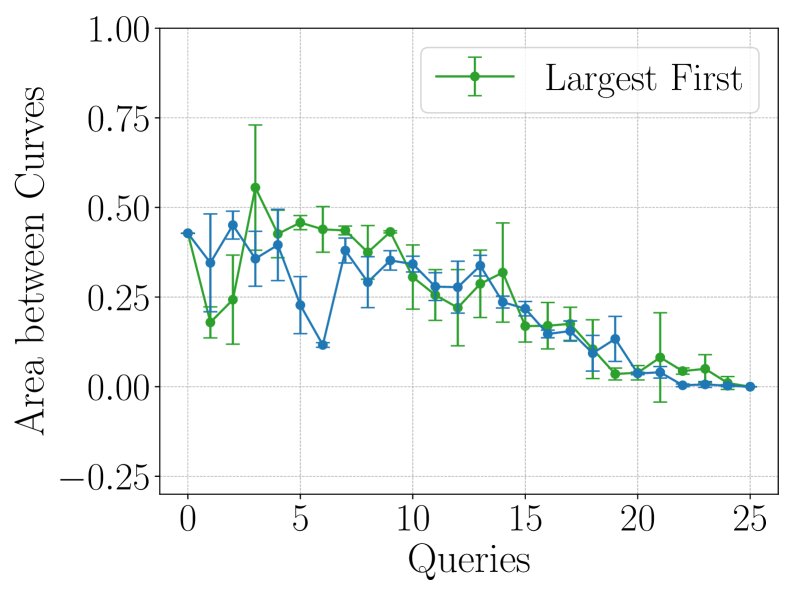
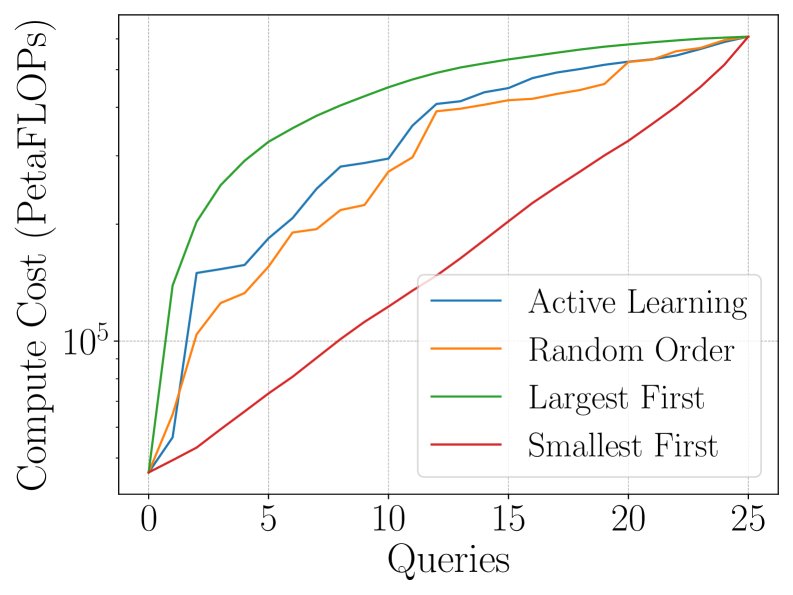
- 不确定性(Uncertainty)采样策略表现最佳。该策略每次选择模型当前预测方差最大的学习曲线进行查询。
- 如下图所示,\(Uncertainty\) 策略(红色)能够持续、稳定地降低AbC值,并且其预测的标准差(阴影区域)远小于随机(Random)等其他策略。
- 这表明,结合主动学习,该框架能够以极高的成本效益,快速收敛到准确的缩放定律。
最终结论
本文成功证明,通过将NLP学习曲线数据集构建为层级结构,并利用潜变量多输出高斯过程进行建模,可以有效地实现学习曲线的零样本预测。该框架不仅能够以显著降低的计算成本推导出可靠的概率性缩放定律,还能通过结合主动学习中的不确定性采样策略,进一步优化数据采集效率,为大型模型的研究和开发提供了宝贵的降本增效工具。