零数据也能自我进化：Agent0让8B模型推理能力暴涨24%

在没有一条人工标注数据的前提下，只靠“自己出题、自己做题”，还能把一个普通的8B Base模型的数学推理拉高18%、通用推理拉高24%，这听上去像是 AI 圈的“永动机”。

ArXiv URL：http://arxiv.org/abs/2511.16043v1

Agent0 这篇工作，就是在严肃尝试这件事。

它把一个基础 LLM 一分为二：一半变成出题老师（Curriculum Agent），一半变成解题学生（Executor Agent），再给学生配上代码解释器等工具，让师生在一个闭环里互相“卷”：学生越会用工具，老师就被逼着出越难、越依赖工具的题目；题目越刁钻，学生就越需要升级推理策略。整个过程不依赖任何外部数据集、也不需要人类打标签。

下面分几步拆解 Agent0 的关键设计。

---

核心问题：自博弈为什么会“学不动”？

过去很多 自进化（self-evolution）/自博弈（self-play） 框架，看起来也很美：

• 模型自己出题，自己解题；

• 靠 $self\text{-}consistency$ 等启发式信号给自己打分；

• 用 RL 反复迭代。

问题有两个致命点：

1. 难度天花板

   模型只能基于自己现有的知识出题，很难生成真正“超纲”的任务。

   出题难度被模型能力“死死按住”，一轮之后就容易停滞。

2. 单轮交互过于简单

   只玩“单问单答”，无法逼迫模型学会真正有难度的能力，比如：

   • 长链式推理；

   • 多步工具调用；

   • 上下文强依赖的对话场景。

结果就是：

题不够难 → 学不到新东西 → 出不出得出更难的题 → 训练停滞。

Agent0 的目标，就是打破这个双重瓶颈。

---

框架总览：两代理共生竞争的“螺旋升级”

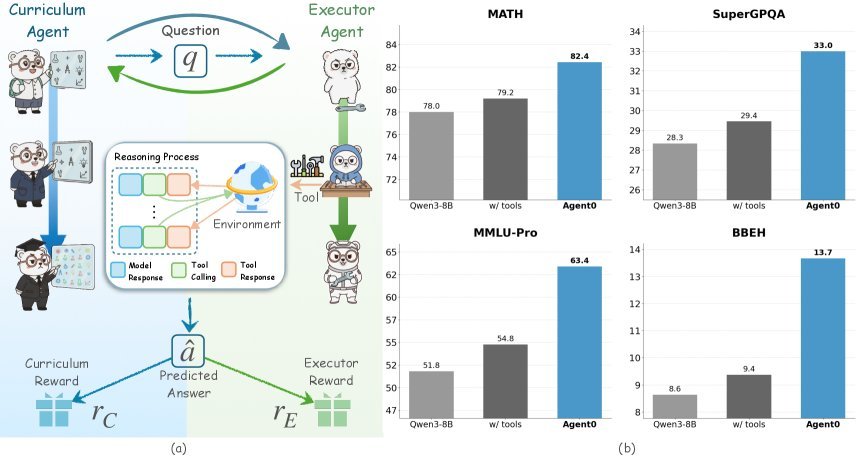
Agent0 的整体思路可以总结为一句话：

用 RL 驱动的“老师出题 + 学生解题 + 工具加持”，让两者在一个闭环中共生竞赛，螺旋式抬高题目难度与解题能力。

两个核心角色

1. Curriculum Agent $\pi_{\theta}$：出题老师

   • 目标：为当前的学生生成前沿任务（frontier tasks）；

   • 训练方式：用 RL（GRPO / PPO 风格）优化“题目质量奖励”。

2. Executor Agent $\pi_{\phi}$：解题学生

   • 目标：解决老师出的任务；

   • 训练方式：用 RL（改进版 ADPO）在这些任务上提升策略。

两者都从同一个 Base LLM 初始化，例如 $Qwen3\text{-}8B\text{-}Base$。

工具闭环的关键作用

Executor 被接上了一个代码解释器工具：

• 题目里若出现 ``\(python ...\)`$$，模型可以执行代码；

• 工具返回 \(`\)output…$$``，再被纳入后续推理。

这件事非常关键：

• 工具提升了学生的实际“算力”和可解题空间；

• 老师能观察到学生调用工具的行为，于是可以主动出更多“必须用工具才能做”的题；

• 工具 → 解题能力提升 → 题目变难、变复杂 → 再逼迫工具更高阶使用。

这样，题目难度就不再仅受模型固有知识的限制，而是借助工具打穿天花板。

---

第一阶段：老师如何学会“出刁钻好题”？

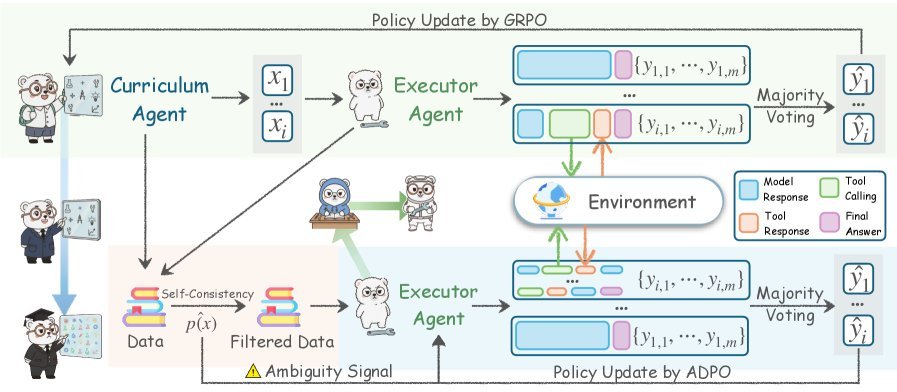
Curriculum Agent 的任务，是生成一个任务描述 $x$，让当前的 Executor 感到“既难又值得学”。

论文把“好题”形式化为一个复合奖励 $R_C(x)$，核心包含三部分：

1. 不确定性奖励 $R_{\text{unc}}$

直觉：

对学生来说，最有学习价值的题，是那种“似懂非懂”的题，而不是：

• 一眼秒杀（太简单），或

• 完全抓瞎（太难）。

做法：

• 对每个任务 $x$，Executor 采样 $k$ 个回答 ${o_i}_{i=1}^k$；

• 找到多数答案 $\tilde{y}$；

• 计算自一致性：

  \[\hat{p}(x)=\frac{1}{k}\sum\_{i=1}^{k}\mathbb{I}(o\_{i}=\tilde{y})\]

• 再将其转成“不确定性奖励”：

  \[R\_{\text{unc}}(x;\pi\_{\phi})=1-2 \mid \hat{p}(x;\pi\_{\phi})-0.5 \mid\]

解释：

• $\hat{p}\approx 0.5$ → 一半对一半错 → 模型非常纠结，这类题奖励最高；

• $\hat{p}\approx 0$ 或 $1$ → 要么不会，要么太会 → 奖励低。

2. 工具使用奖励 $R_{\text{tool}}$

为了鼓励“出那种必须用工具才能解决”的题：

\[R\_{\text{tool}}(x;\pi\_{\phi})=\gamma\cdot\min(N\_{\text{tool}}(y),C)\]

• $N_{\text{tool}}(y)$ 是回答里工具调用次数；

• 设定上限 $C$，避免无意义“刷工具”。

这让老师在 RL 中学会一个倾向：题目要能逼学生调用工具，否则奖励偏低。

3. 去重复惩罚 $R_{\text{rep}}$

为了防止老师“刷套路题”，论文引入重复惩罚：

\[R\_{\text{rep}}(x\_{i})=\lambda\_{\text{rep}}\frac{ \mid C\_{k} \mid }{B}\]

• $C_k$：与当前题 $x_i$ 过于相似的题目集合；

• $B$：一个 batch 中的总题数。

这样可以鼓励生成更加多样化的任务。

最终组合奖励：

\[\small R\_{C}(x\_{i})=R\_{\text{format}}(x\_{i})\cdot\max\Big(0,\big(\lambda\_{\text{unc}}R\_{\text{unc}}+\lambda\_{\text{tool}}R\_{\text{tool}}\big)-R\_{\text{rep}}(x\_{i})\Big)\]

这个 $R_C$ 作为 RL 算法 GRPO 中的奖励，指导 Curriculum Agent 学出一个自动“找学生短板+逼学生用工具”的出题策略。

---

第二阶段：学生如何在“无标签”下自我强化？

Curriculum Agent 训练好一轮后，会被冻结，用来大规模出题：

1. 老师生成候选任务池 $X_{\text{pool}}$；

2. 学生针对每个题 $x$，采样 $k$ 条完整解题轨迹；

3. 用这些轨迹构建一个“高价值训练集” $\mathcal{D}^{(t)}$。

1. 用自一致性筛选“有价值的难题”

仍然用 $\hat{p}(x)$ 度量自一致性，然后只保留那些既不太简单也不太绝望的题：

\[\mathcal{D}^{(t)}=\{x\in X\_{\text{pool}}\mid \mid \hat{p}(x;\pi\_{\phi}^{(t-1)})-0.5 \mid \leq\delta\}\]

也就是：

• $\hat{p}$ 接近 $0.5$；

• 在文中设置为 $0.3\sim0.8$ 范围。

这些题通常是模型正在“模棱两可”阶段的知识盲区，最适合作为训练数据。

2. 多答案多数票 → 伪标签

对每个任务 $x$：

• 将 $k$ 个回答中的多数答案 $\tilde{y}$ 当成“伪标签”；

• 对每条轨迹 $i$，定义终止奖励：

  \[R\_{i}=\mathbb{I}(o\_{i}=\tilde{y})\]

本质上是：

• 谁跟多数派站在一起，谁得到奖励；

• 但题目本身没有人工标签，全靠模型自己“投票定输赢”。

3. ADPO：在“含糊题”上更谨慎的 RL

标准的 GRPO / PPO 默认所有样本同等可靠，但在这里：

• 伪标签来自多数票，存在明显 label noise；

• 模型对有些题极度不确定（$\hat{p}$ 接近 0.5），探索价值高，但标签噪声也更大。

为此，论文提出 ADPO（Ambiguity-Dynamic Policy Optimization），基于 $\hat{p}(x)$ 对学习过程做两件事：

1. 按歧义程度缩放优势 $\tilde{A}_i(x)$

   含糊题（高不确定性）和确定题，被赋予不同权重，避免噪声样本在梯度中“喊得过大声”。

2. 动态调整策略更新上界 $\epsilon_{\text{high}}(x)$

   在 PPO 风格的 clipping 中：

   \[\small\mathcal{L}\_{\text{ADPO}}(\theta)= \mathbb{E}\_{x\sim D^{(t)}}\Bigg[-\frac{1}{G}\sum\_{i=1}^{G}\min\Big(r\_{i}(\theta)\tilde{A}\_{i}(x), \text{clip}\big(r\_{i}(\theta),1-\epsilon\_{\text{low}},1+\epsilon\_{\text{high}}(x)\big)\tilde{A}\_{i}(x)\Big)\Bigg]\]

   • 当 $\hat{p}(x)$ 表示题目很含糊时，$\epsilon_{\text{high}}(x)$ 会更小；

   • 代表对策略更新更保守，避免被噪声伪标签带偏。

总结一下：

ADPO 利用“不确定性信号”决定对哪类题激进探索、对哪类题保守更新，从而在“完全无标签”的场景下维持 RL 的稳定性与有效收益。

---

多轮对话与工具融合：接近真实问题求解

除了单轮问答，Agent0 还支持多轮交互任务：

• Curriculum Agent 可以生成带上下文的对话式任务；

• Executor 需要在多轮对话中规划何时提问、何时调用工具、何时给出结论。

而代码解释器工具贯穿始终，使得任务可以自然演化为：

• 用自然语言推理拆解问题；

• 使用 Python 验证中间猜想；

• 多轮来回修正错误。

论文给出的定性分析案例显示，在迭代到第 3 轮时，任务已经从简单几何题进化到复杂约束求解，需要混合语言推理 + 程序搜索 + 多步验证。

---

实验结果：从数学到通用推理的迁移收益

论文在两个 Base 模型上评估：$Qwen3\text{-}4B\text{-}Base$ 与 $Qwen3\text{-}8B\text{-}Base$，训练过程 全程不使用人工标注数据。

1. 数学推理：+18% 提升

在 AMC、MATH、GSM8K、Olympiad-Bench、AIME24/25 等多个数学基准上：

• Agent0 显著优于其他自进化基线和数据自由方法；

• 在 $Qwen3\text{-}8B$ 上，数学推理平均提升约 18%。

这类任务天然适合“工具 + 多步推理”，也最能体现 co-evolution 的收益。

2. 通用推理：+24% 提升

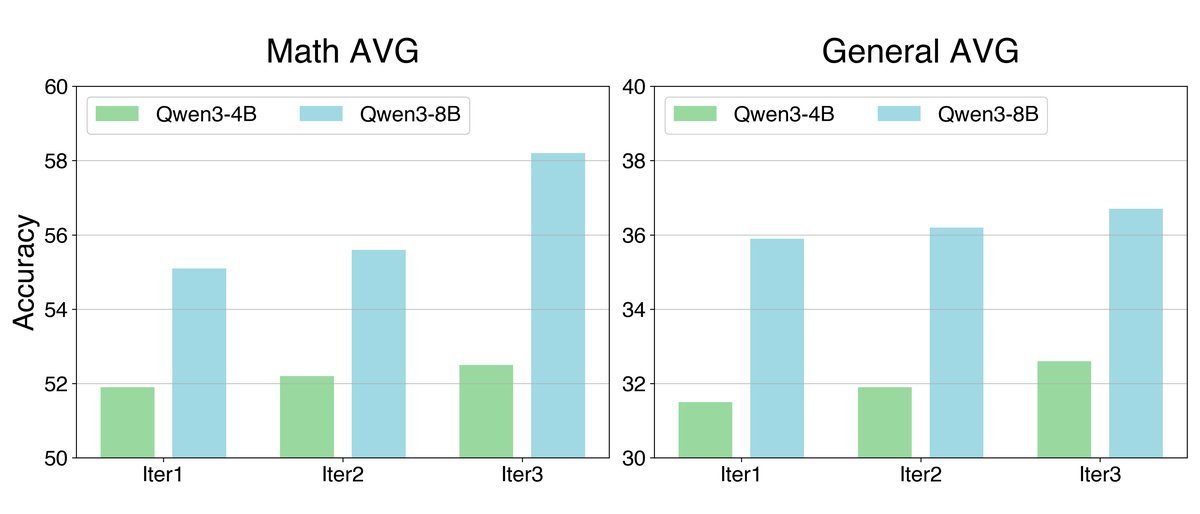
在 SuperGPQA、MMLU-Pro、BBEH 等更偏通识与复杂推理的基准上：

• 使用 Agent0 训练过的 Executor，在 未见过的通用任务上仍然收益明显；

• $Qwen3\text{-}8B$ 的通用推理平均提升约 24%。

这说明：

通过“自出题 + 工具增强推理”学到的能力，并非仅限于数学，而是对整体思维链条与决策策略都带来了迁移。

---

关键洞见与工程启示

从工程视角看，Agent0 带来了几条值得注意的启发：

1. 有工具参与的自进化，可以打穿模型知识上限

   单纯靠语言模型互博，题目很难越过已有知识边界；

   接工具之后，“会写代码”与“会思考用不用代码”变成新的学习维度。

2. “难度适中 + 高不确定性”的题目最值得花算力训练

   通过 $\hat{p}(x)$ 这一简单指标，就能自动挑出“正在学、还不会”的题区间，

   这比粗暴地用所有自生成数据训一遍更有效。

3. 无标签 RL 要高度重视不确定性建模

   ADPO 不是引入更复杂的 reward，而是利用 $\hat{p}(x)$ 去调节：

   • 优势函数权重；

   • PPO 的 clip 范围。

   这种“让优化器知道哪些样本不靠谱”的做法，对任何 self-training 框架都具有借鉴意义。

4. 多轮对话 + 工具使用是未来 Agent 能力的训练核心场景

   单轮问题解决已经很难拉开差距；

   能否在真实复杂环境下规划调用工具、保持长链推理一致性，将成为下一代 Agent 的关键。

---

小结

Agent0 提出了一种完全不依赖人类标注的自进化框架，通过：

• 双代理共生竞争（Curriculum vs Executor）；

• 工具集成的推理闭环（尤其是代码解释器）；

• 以不确定性为核心信号的任务筛选与 RL 优化（$R_{\text{unc}}$、ADPO）；

在 8B 规模的 Base 模型上，实打实地拿到了 数学推理 +18%、通用推理 +24% 的提升。

在“人工数据愈发昂贵、模型愈发渴望长尾能力”的当下，这种从零数据出发、让模型自己进化自己的路线，很可能会成为下一阶段 LLM Agent 训练的重要方向之一。