AI Progress Should Be Measured by Capability-Per-Resource, Not Scale Alone: A Framework for Gradient-Guided Resource Allocation in LLMs
-
ArXiv URL: http://arxiv.org/abs/2511.01077v1
-
作者: Yulun Wu; David McCoy
-
发布机构: Capital One; University of California, Berkeley
TL;DR
本文主张用“单位资源能力”而非单纯的规模来衡量AI进展,并提出了一个基于梯度指导资源分配的理论框架,通过识别和优先利用高影响力的参数和数据,来显著提升大语言模型(LLM)生命周期中的效率。
关键定义
- 单位资源能力 (Capability-Per-Resource):本文提出的核心评估指标,衡量每单位资源(如GPU小时、能耗)投入所带来的性能提升,即 $\Delta\Psi/\Delta\Gamma$。该指标旨在将AI发展的目标从追求绝对性能转向追求资源效率。
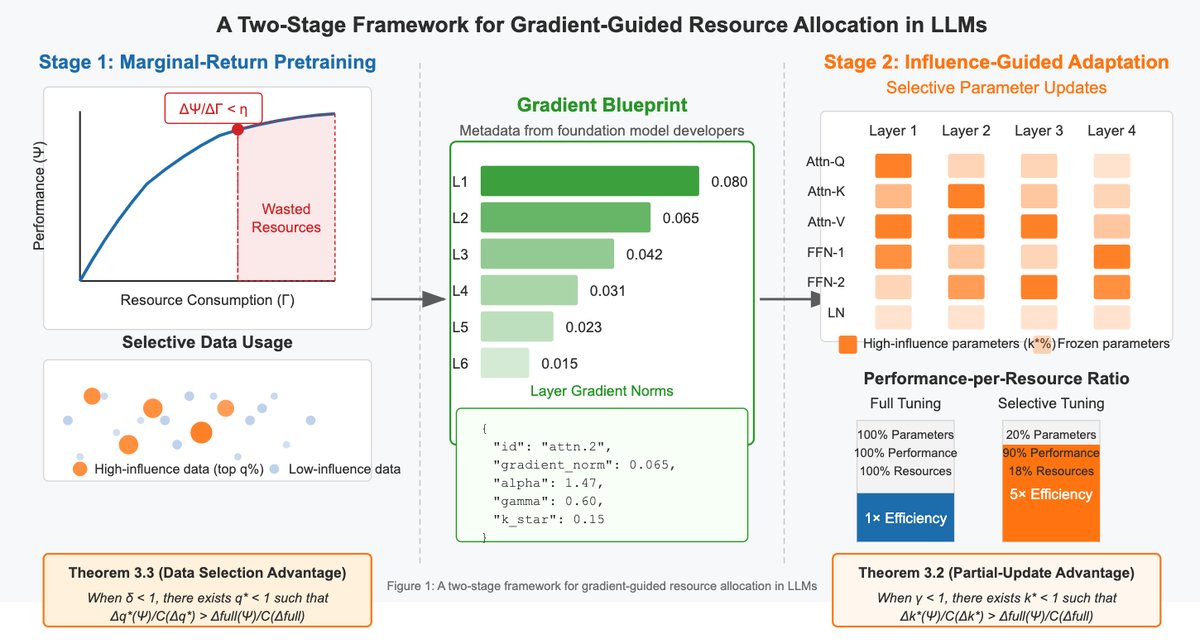
- 梯度蓝图 (Gradient Blueprints):与模型权重一同发布的元数据,它记录了模型在代表性任务上各个子模块(submodule)的梯度范数等统计信息。其目的是为下游用户揭示哪些模型组件对特定任务最“有影响力”,从而指导他们进行高效的参数选择和微调。
- 规模原教旨主义 (Scaling Fundamentalism):本文用来描述当前AI研究领域中一种主流趋势,即认为仅通过不断增大模型规模和计算投入就能带来能力提升,而往往忽略了资源效率和可持续性。
- 部分更新优势 (Partial-Update Advantage):本文提出的一个理论概念,指在梯度呈重尾分布(heavy-tailed distribution)的现实情况下,仅更新一小部分高影响力的参数,在“单位资源能力”这一指标上,其效率严格优于对所有参数进行完整微调。
相关工作
当前AI领域,尤其是大语言模型的发展,被“规模原教旨主义”所主导。研究遵循“Chinchilla”等伸缩法則 (scaling laws),追求更大的模型和更多的数据,这带来了巨大的成功,但也导致了高昂的环境成本和资源鸿沟,形成了少数资源雄厚的机构开发基础模型,而广大研究社区在资源受限下进行适配的“计算寡头”局面。
为应对资源限制,研究界开发了多种效率提升技术。参数高效微调 (Parameter-Efficient Fine-Tuning, PEFT) 方法如LoRA、QLoRA和Adapters通过只更新一小部分参数来降低内存和计算开销。模型压缩技术如剪枝 (pruning) 和注意力头移除在训练后削减模型冗余部分。数据效率方面的研究则包括重要性采样和课程学习等。
本文旨在解决的 конкретно问题是:尽管存在上述各种效率提升方法,但它们大多被视为资源不足时的“权宜之计”或“工程技巧”,缺乏一个统一的理论框架来解释其有效性。此外,参数效率和数据效率的研究常常彼此独立,并且缺乏一种将基础模型开发者(拥有资源)的洞察系统性地传递给下游模型适配者(资源受限)的机制。本文的目标就是建立这样一个理论框架,将选择性更新从“技巧”提升为“原则”,并提出“梯度蓝图”作为实现这一目标的实用工具。
本文方法
本文提出了一个以资源意识为核心的LLM开发和评估框架,其核心思想是最大化“单位资源能力” ($\Delta\Psi/\Delta\Gamma$)。该框架分为两个层面:一个适用于基础模型开发者和下游适配者的两阶段范式,以及支撑该范式的理论基础。
两阶段开发范式
本文框架针对AI生态中的两类主要参与者设计了不同的策略:
-
基础模型开发者 (Foundation Model Developers):在预训练阶段,开发者应采用“边际回报预训练” (marginal-return pretraining) 策略。具体而言,他们应持续监控单位资源带来的性能提升 ($\Delta\Psi/\Delta\Gamma$),当该比率在一定窗口内持续低于预设阈值 $\eta$ 时,便停止训练。这一策略避免了在收益递减阶段浪费大量计算资源。训练完成后,开发者不仅发布模型权重,还应发布梯度蓝图 (Gradient Blueprints)。
-
模型适配者 (Model Adapters):下游用户在资源受限的情况下,利用梯度蓝图进行“影响力指导的适应” (influence-guided adaptation)。蓝图揭示了哪些模型子模块(如特定层的注意力块或前馈网络)对相关任务的梯度贡献最大。适配者只需选择性地微调这些高影响力的参数(例如,仅占总参数10-20%),就能在极低的资源成本下实现接近全量微调的性能,从而大幅降低了内存和计算开销。
这一范式通过梯度蓝图在开发者和适配者之间架起了一座桥梁,实现了效率知识的传递。
理论基础
本文为上述框架提供了坚实的理论依据,证明了选择性更新并非妥协,而是在特定条件下的最优策略。
部分参数更新优势
理论核心: 在梯度分布呈重尾(或幂律)特性的模型中(这在Transformer中很常见),仅更新一小部分参数在“单位资源能力”上比全量更新更优。
许多LLM的梯度分布遵循幂律 (power-law) Decay,即第 $r$ 大的梯度范数 $\ \mid \nabla_{\theta_{(r)}}\ \mid \approx Cr^{-\alpha}$(其中 $\alpha>1$)。这意味着一小撮参数占据了绝大部分梯度量。因此,只更新这部分“高影响力”参数(例如前 $k\%$),可能只用 $k\%$ 的资源就获得了远大于 $k\%$ 的性能提升。 本文从理论上证明,存在一个最优的更新比例 $k^*$,使得部分更新的资源效率严格高于全量更新:
\[\frac{\Delta_{k^{*}}(\Psi)}{\mathcal{C}(\Delta_{k^{*}})} > \frac{\Delta_{\mathrm{full}}(\Psi)}{\mathcal{C}(\Delta_{\mathrm{full}})}\]这一结论将LoRA等PEFT方法从工程技巧,提升到了理论上最优的资源分配策略。
用简单梯度近似影响力
理论核心:昂贵的二阶影响力计算(如Hessian矩阵)可以用简单的一阶梯度范数 $\ \mid \nabla_{\theta_i}\ \mid $ 来有效近似。
确定哪些参数是“高影响力”的,最精确的方法是计算二阶导数,但这在LLM中计算成本极高。本文证明,在Fisher信息矩阵近似下,参数对性能的真实影响力与它的一阶梯度范数近似成正比。因此,通过计算并排序梯度范数,就可以高效且准确地识别出最重要的参数。这为通过梯度蓝图发布梯度范数统计信息提供了理论合理性。
数据选择与交叉影响力
理论核心: 效率增益可以在参数和数据两个维度上实现,并且两者结合可以产生乘法效应。
与参数类似,不同训练数据点对模型更新的贡献也极不均衡(即数据影响力也呈重尾分布)。通过识别并优先使用那些能产生最大梯度更新的“高影响力”数据样本,可以进一步提升训练效率。
本文更进一步提出了交叉影响力 (cross-influence) 的概念,定义为张量 $T_{i,j}=\left \mid \frac{\partial L(z_j;\theta)}{\partial\theta_i}\right \mid $,它描述了数据样本 $z_j$ 对参数 $\theta_i$ 的具体影响。当同时选择高影响力的参数和高影响力的数据进行更新时,资源效率的提升是乘法级的。例如,如果保留20%的参数能达到80%的性能,保留30%的数据能达到90%的性能,两者结合可能用 $20\% \times 30\% = 6\%$ 的资源达到 $80\% \times 90\% = 72\%$ 的性能,实现超过10倍的单位资源效率提升。
实验结论
本文是一篇立场与理论框架论文,其主要贡献在于提出了一个全新的评估与开发范式,并为其提供了数学基础。因此,文章的结论主要源于理论分析,而非大规模的实证实验。文章末尾提到的具体案例研究(如生物医学适配)未能完整展示。
本文的核心结论如下:
-
理论有效性:文章从理论上证明了,在梯度呈重尾分布(这在Transformer中很常见)的条件下,部分更新策略(partial updates)在“单位资源能力”指标上严格优于全量更新策略。这为PEFT等方法的成功提供了坚实的数学解释,并将其从“硬件限制下的妥协”转变为“理论上更优的资源分配策略”。
-
方法可行性:通过证明简单的一阶梯度范数可以作为参数影响力的有效代理,本文为“梯度蓝图”这一实践工具提供了理论支持。开发者无需进行复杂的二阶计算,只需记录并发布易于获取的梯度统计信息,就能为下游用户提供极具价值的指导。
-
效率的乘法效应:本文揭示了LLM训练中存在参数和数据两个维度的冗余。通过协同进行参数选择和数据选择,可以实现效率的乘法级提升,从而可能将资源需求降低几个数量级。
最终,本文得出结论:AI领域应从“唯规模论”转向以“单位资源能力”为核心的评估体系。通过采纳本文提出的梯度指导的资源分配框架和“梯度蓝图”等实践工具,AI社区可以在推动技术进步的同时,构建一个更加可持续、公平和高效的未来,让更多资源有限的研究者也能参与到前沿AI的开发与创新中。