An Augmentation Overlap Theory of Contrastive Learning
-
ArXiv URL: http://arxiv.org/abs/2511.03114v1
-
作者: Yifei Wang; Qi Zhang; Yisen Wang
-
发布机构: MIT; Peking University
TL;DR
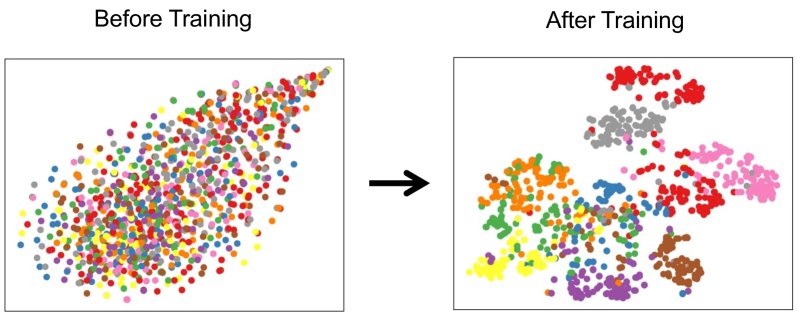
本文提出了一个“增强重叠”（Augmentation Overlap）理论，通过揭示同一类别的不同样本在数据增强下会产生重叠的视图，解释了实例级别的对比学习为何能学习到具有类别区分性的表示，并基于此推导出了更紧密的下游任务性能界。
关键定义
本文的核心理解建立在对以下概念的阐述和更新上：
- 条件独立性假设 (Conditional Independence Assumption)：这是一个在先前理论研究中被广泛采用的假设，它假定给定一个样本的真实标签，通过不同数据增强生成的视图（即正样本对）是相互独立的。本文指出这个假设在现实中难以成立，因为数据增强的效果通常与输入样本自身内容相关。
- 增强重叠 (Augmentation Overlap)：这是本文提出的核心理论。其核心观点是，强有力的数据增强会使得来自同一类别（Intra-class）的不同样本，其增强后视图的支撑集（support）产生重叠。例如，不同汽车的图片可能都会被裁剪出相似的轮胎视图。因此，当对比学习将正样本对（同一张图的两个增强视图）拉近时，也间接地将那些拥有重叠视图的同类样本聚集在一起，从而实现了类级别的区分。
-
平均分类器 (Mean Classifier)：为了便于理论分析，本文采用的一种线性分类器。其权重向量 \(w_y\) 直接使用该类别所有样本在表示空间中的平均表示 \(μ_y\)，即 $$w_y = μ_y = E_{p(x y)}[f(x)]$$。下游任务的性能通过该分类器在交叉熵损失下的表现来衡量。
相关工作
自监督对比学习通过拉近同一样本的增强视图（正样本）并推开不同样本的视图（负样本），在各种任务上取得了与监督学习相媲美的性能。然而，其工作机制的理论解释尚不清晰。
当前存在的关键问题是：为什么旨在进行实例级别区分的对比学习，最终能学习到对类别级别下游任务有效的表示？
- 现有理论的瓶颈：
- 早期的理论（如 Arora et al.）依赖于不切实际的“条件独立性假设”，并且其推导的性能上界错误地暗示了增加负样本数量会有损性能，这与经验观察相悖。
- 另一类理论（如 Wang & Isola）将对比学习的目标分解为正样本的“对齐性”（alignment）和负样本的“均匀性”（uniformity）。然而，本文认为仅有对齐性和均匀性不足以保证良好的下游性能，数据增强策略（即正样本对的选择）至关重要。
- 本文的目标： 本文旨在解决上述理论与实践的脱节问题。首先，通过引入新的分析技术，在既有的条件独立性假设下推导出更紧密的性能界，正确地反映了增加负样本数量的益处。其次，也是更核心的，提出“增强重叠”这一更现实的假设来取代条件独立性假设，从而为对比学习的成功提供一个更根本、更具解释力的理论框架。
本文方法
本文的理论贡献分为两个主要部分：首先改进了基于旧有假设的界，然后提出了全新的增强重叠理论。
改进：基于条件独立假设的更紧密性能界
在挑战条件独立性假设之前，本文首先展示了即便在该假设下，通过更精细的分析技术也能得到远优于先前工作的性能界。
-
创新点：负样本的蒙特卡洛视角 与以往将负样本视为“类别碰撞/覆盖”的视角不同，本文创新地指出，InfoNCE损失中的负样本项可以被看作是下游监督损失（mCE loss）负样本项的一个蒙特卡洛（Monte Carlo）估计。 具体来说，通过应用琴生不等式（Jensen’s inequality），可以证明对比损失的负样本部分 $\bar}_{\rm contr}^{-}(f)$ 是下游损失负样本部分 $\bar}_{\rm mCE}^{-}(f)$ 的一个蒙特卡洛估计 $\bar}_{\rm MC}(f)$ 的下界：
\[\bar{{\mathcal{L}}}\_{\rm contr}^{-}(f) \geq \mathbb{E}\_{\Pi\_{i}p(y^{-}\_{i})}\log\frac{1}{M}\sum\_{i=1}^{M}\exp(f(x)^{\top}\mu\_{y^{-}\_{i}})=\bar{{\mathcal{L}}}\_{\rm MC}(f)\]这个估计的误差会随着负样本数量 $M$ 的增加而减小，其误差界为 $ \mid \bar}_{\rm MC}(f)-\bar}_{\rm mCE}^{-}(f) \mid \leq\frac{e}{\sqrt{M}}$。
-
更紧密的界 (Theorem 4.3) 基于上述分析，本文推导出了新的下游性能上下界：
\[\bar{\mathcal{L}}\_{\rm contr}(f)-\frac{1}{2}{\operatorname*{Var}(f(x)\mid y)}-\frac{e}{\sqrt{M}} \leq \bar{\mathcal{L}}\_{\rm mCE}({f}) \leq \bar{\mathcal{L}}\_{\rm contr}({f})+\frac{e}{\sqrt{M}}\]这个结果的重大意义在于，误差项 $\frac{e}{\sqrt{M}}$ 随着负样本数量 $M$ 的增大而趋于零。这首次从理论上证明了增加负样本数量的益处，解决了以往理论与实践的矛盾，并表明当 $M \to \infty$ 时，对比损失与监督损失是渐近等价的。
| 方法 | 上界 ${\mathcal{L}}_{\rm sup}(f) \leq {\mathcal{L}}_{\rm unsup}(f) + \text{Error}$ |
|---|---|
| Arora et al. (2019) | $O(\log\frac{M}{K}) - \log (1-\tau_M) + \mathrm{Col}$ |
| Von Kügelgen et al. (2021) | $\log\frac{N\tau + (1-\tau)(M-1)}{K}$ |
| HaoChen et al. (2021) | $\frac{\epsilon_{\text{align}}}{2} + 2 \log 2$ |
| 本文 | $\frac{e}{\sqrt{M}}$ |
核心：增强重叠理论
本文最重要的贡献是提出了“增强重叠”理论，以取代不切实际的条件独立性假设。
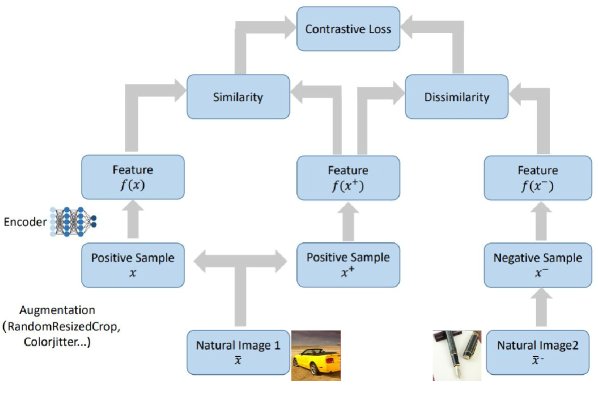
(a) 对比学习框架。 (b) 来自ImageNet的四张图片的增强视图。前两行是汽车，后两行是笔。第一列是锚点样本，2-5列是其对应的增强视图。可见，不同汽车（同类）可能产生相似的局部视图（如轮胎），而汽车和笔（异类）的视图则差异明显。
-
创新点：从实例关联到类别聚合 该理论的核心洞察是：数据增强是连接同类样本的桥梁。虽然对比学习的目标是拉近“同一个样本”的两个不同视图，但由于强数据增强（如随机裁剪、颜色抖动等）的存在，来自“不同样本但属于同一类别”的图片也可能生成非常相似的视图（如上图所示的不同汽车的轮胎）。这种由增强产生的视图“重叠”，使得优化器在拉近正样本对的同时，也间接地将这些共享相似视图的同类样本拉近。
-
优点
- 更真实：该理论不再依赖于难以满足的条件独立性假设，而是关注数据增强这一对比学习成功的关键实践因素，为理论与实践之间建立了更坚实的联系。
- 更具解释力：它清晰地解释了为什么一个旨在区分“实例”的任务，最终能够学习到“类别”结构。这个过程是通过增强重叠作为媒介，将实例级别的吸引力传导至类别内部。
- 指导实践：该理论强调了数据增强策略的重要性。增强的强度需要恰到好处：足够强以在同类样本间创造重叠，但又不能过强以至于在不同类别样本间也产生重叠（例如，将汽车的轮子和披萨饼错误地视为相似），从而为设计和选择数据增强策略提供了理论指导。
实验结论
尽管本文主要是一篇理论性很强的论文，所提供的文本片段未包含完整的实验章节，但其理论推导和观点由以下几方面得到支撑：
- 理论验证：
- 本文提出的上下界在理论上优于先前所有工作。一个对比图（原文Fig 3，未在提供文本中显示但有提及）经验性地展示了本文的理论上界随着负样本数$M$的增加而收紧，而其他理论的界则发散或保持不变，验证了本文理论的准确性。
- 定理4.3的推导解决了先前理论中“负样本越多，性能界越差”的悖论，与“对比学习受益于大量负样本”的经验观察完全一致。
- 理论的应用：
- 基于增强重叠理论，本文提出了一个名为GARC的无监督模型选择指标。该指标通过量化增强重叠的程度来评估表示的质量，无需访问带标签的下游数据即可进行模型评估和选择。这证明了该理论不仅具有解释力，还具有切实的实践价值。
- 最终结论： 本文通过提出“增强重叠”理论，为自监督对比学习的成功提供了一个更坚实、更贴近实践的理论基础。该理论不仅修正了旧有理论的缺陷，推导出了迄今最紧密的性能界，还指出了数据增强在构建类别结构中的核心作用，并催生了实用的无监督模型评估工具。这标志着对对比学习工作机制的理解迈出了重要一步。