Deep sequence models tend to memorize geometrically; it is unclear why

TL;DR

本文通过一个精心设计的实验揭示，深度序列模型在记忆事实时并非简单地存储局部关联，而是会自发形成一种“几何式记忆”结构，这种结构编码了实体间（包括训练中未共现的实体）的全局关系，从而将复杂的多步推理任务简化为易于学习的单步几何问题。

关键定义

本文的核心在于区分并研究了两种记忆范式，它们对于理解模型如何存储和推理知识至关重要：

  1. 关联式记忆 (Associative Memory) 这是文献中对参数化记忆的主流抽象。它将记忆视为一个“查找表”，通过一个权重矩阵（如 ${\bf{W}}_{\tt assoc}$）存储训练期间共同出现的实体（如 $u$ 和 $v$）之间的关联强度。在这种视图下，实体本身的嵌入 ${\bf{\Phi}}$ 可以是任意的，知识检索依赖于矩阵运算，例如查询 ${\bf{\Phi}}(v)^{T}{\bf{W}}_{\tt assoc}{\bf{\Phi}}(u)$ 的值。这种记忆只编码局部共现信息。

  2. 几何式记忆 (Geometric Memory) 这是本文提出的用以解释实验现象的另一种记忆范式。它认为记忆并非存储在独立的权重矩阵中，而是直接编码在实体嵌入 ${\bf{\Phi}}_{\tt geom}$ 的几何结构里。这些嵌入被组织得非常有条理，以至于它们之间的几何关系（如点积或距离）能够反映实体间的全局、多跳（multi-hop）关系，即使这些实体从未在训练中一起出现过。

  3. 权重内路径星图任务 (In-weights Path-star Task) 本文设计的一种实验环境，旨在干净地分析参数化记忆。与将图结构作为上下文输入不同，该任务要求模型首先将一个固定图的边（原子事实）“记忆”到其模型权重中，然后基于这些记忆在图上进行路径查找。这迫使模型完全依赖其内部学到的知识结构进行推理。

  4. 隐式推理 (Implicit Reasoning) 指模型利用存储在权重中的知识进行推理，但并不生成明确的、逐步的“思维链”（chain of thought）。模型直接输出最终答案。

相关工作

当前，学术界对神经网络如何记忆原子事实（如名人生日）的主流理解是，模型采用了一种关联式记忆的机制。这种机制可以被抽象为一个简单的查找过程，即存储实体间的共现关系。然而，这种观点难以解释近年来观察到的一些现象：深度模型，特别是 Transformer，在没有明确的分步监督或思维链的情况下，表现出了一定程度的隐式推理能力。

关联式记忆视图的关键瓶颈在于，它无法有效处理需要多步组合（composition）的推理任务。例如，一个需要 $\ell$ 步推理的任务，在关联式记忆框架下，相当于要组合一个矩阵运算 $\ell$ 次。在没有中间步骤监督的情况下，学习这种 $\ell$ 次组合是一个“大海捞针”式的难题，其学习难度随 $\ell$ 呈指数级增长。

本文旨在解决的具体问题是：为什么深度序列模型（如 Transformer 和 Mamba）能够在被设计为极具挑战性的多步推理任务（权重内路径星图任务）上取得成功？本文试图挑战主流的关联式记忆观点，并探究是否存在一种更根本的记忆机制在起作用。

本文方法

实验设计：权重内路径星图任务

为了干净地分离和研究参数化记忆，本文作者设计了一个名为“权重内路径星图任务”的实验。该任务基于一种特殊的图拓扑——路径星图（path-star graph），它由一个根节点和从该根节点分支出去的多条不相交的路径组成。

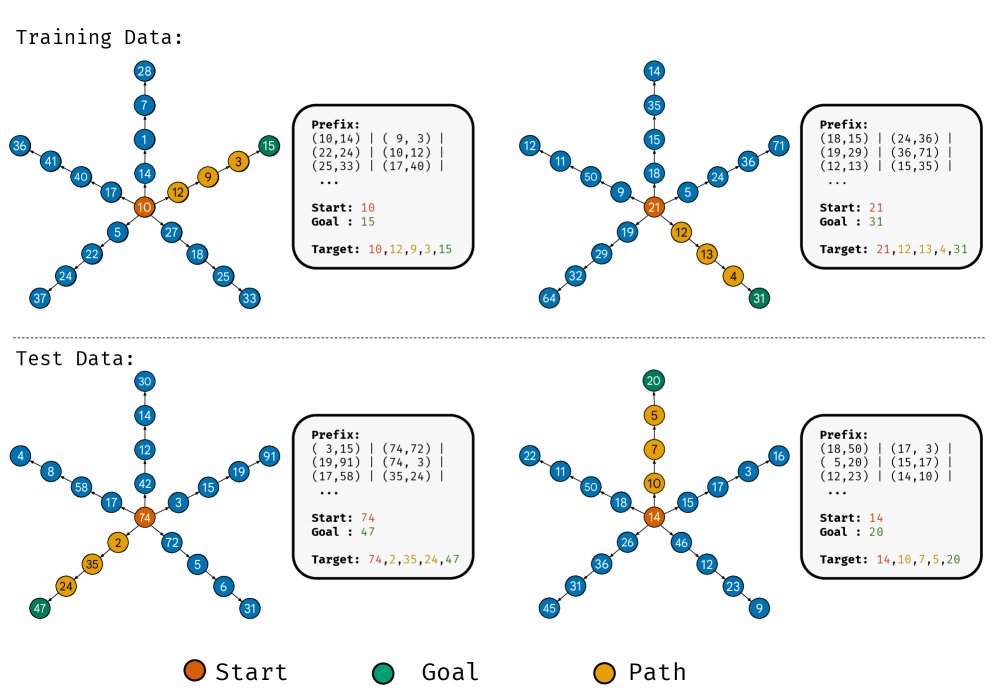
路径星图拓扑结构

与之前研究中将图结构作为上下文输入（in-context）不同，本文的任务范式如下：

  1. 记忆阶段：模型被训练记忆一个固定的路径星图的边。训练样本是图中的一条边，例如输入一个节点 $v$，目标是其相邻节点 $v^{\prime}$。
  2. 推理阶段：模型被给予图中的一个叶子节点 ${v}_{\tt{leaf}}$ 作为输入，要求预测从根节点 ${v}_{\tt{root}}$ 到该叶子节点的完整路径。训练集和测试集分别使用图中不相交的叶子节点子集。

这种“权重内”（in-weights）的设计确保了模型必须依赖其存储在参数中的知识（即对图结构的记忆）来完成推理，而不是依赖于输入的上下文信息。

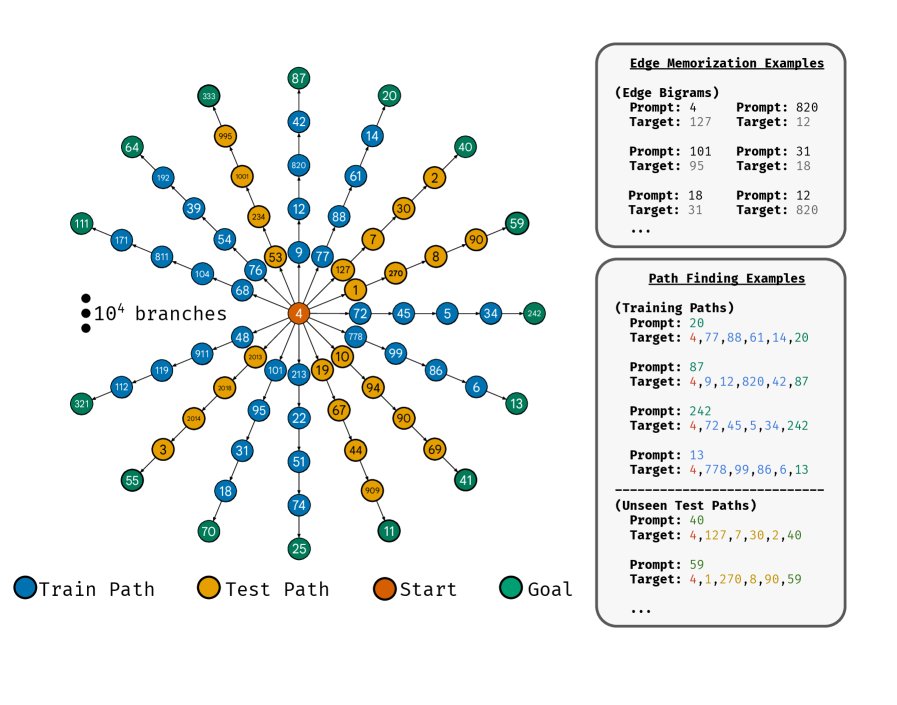
权重内任务的训练和测试示例

核心发现：隐式推理的成功与矛盾

实验首先观察到一个惊人的结果：无论是 Transformer 还是 Mamba 模型，都在这个被设计为对自回归模型极不友好的任务上取得了近乎完美的成功，即使是在包含数千个节点、路径长度达到10的大型图上。这一成功与模型在“上下文内”版本任务中的彻底失败形成鲜明对比。

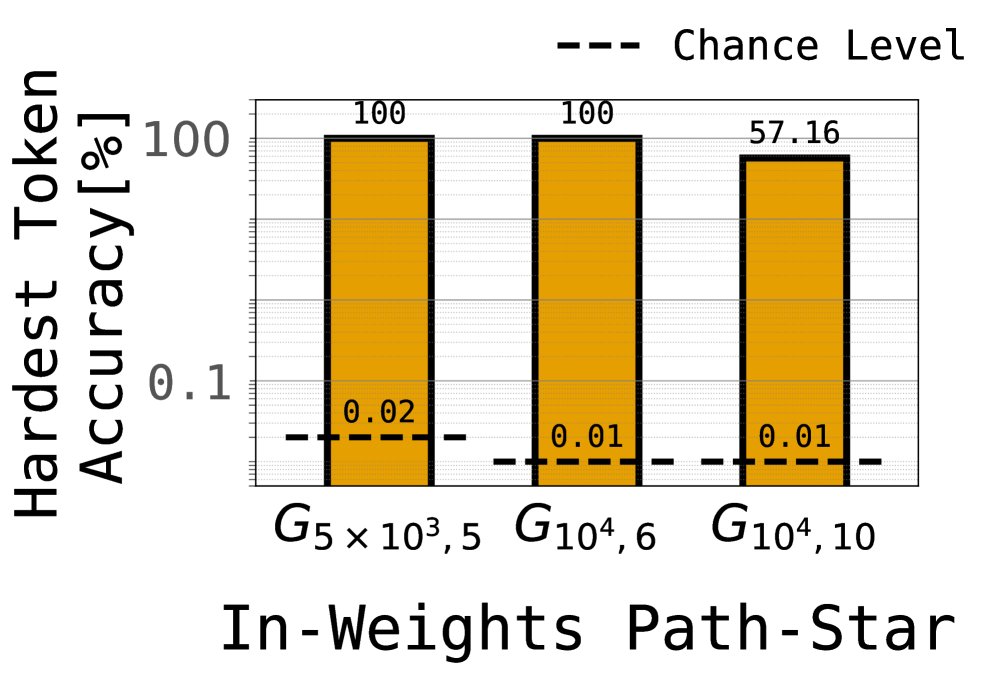在权重内路径星图任务上，Transformer和Mamba均取得成功 左图显示，在不同规模的图上，Transformer 均能达到很高的路径预测准确率。右图显示，即便是只训练模型预测最难的第一个token，模型依然能成功，这直接挑战了关联式记忆的观点。

这个成功引出了一个核心矛盾。按照关联式记忆的观点，预测路径的第一个节点是一个需要 $\ell$ 次组合的推理任务（即从叶子节点回溯 $\ell$ 步到根节点的第一个邻居）。理论和实践都表明，学习这种无中间监督的组合任务极其困难。然而，模型却轻易地学会了。

作者通过实验排除了其他可能的解释（例如模型学会了某种简单的“作弊”策略），最终确认，模型确实解决了这个看似困难的 $\ell$ 次组合问题。

创新点：几何式记忆的提出与佐证

为了解决上述矛盾，本文提出了几何式记忆的核心观点，并论证其在竞争中胜过了关联式记忆。

创新之处在于：本文指出，模型并未将图的边作为孤立的关联事实存储，而是自发地将所有节点组织成一个有意义的几何空间。在这个空间中：

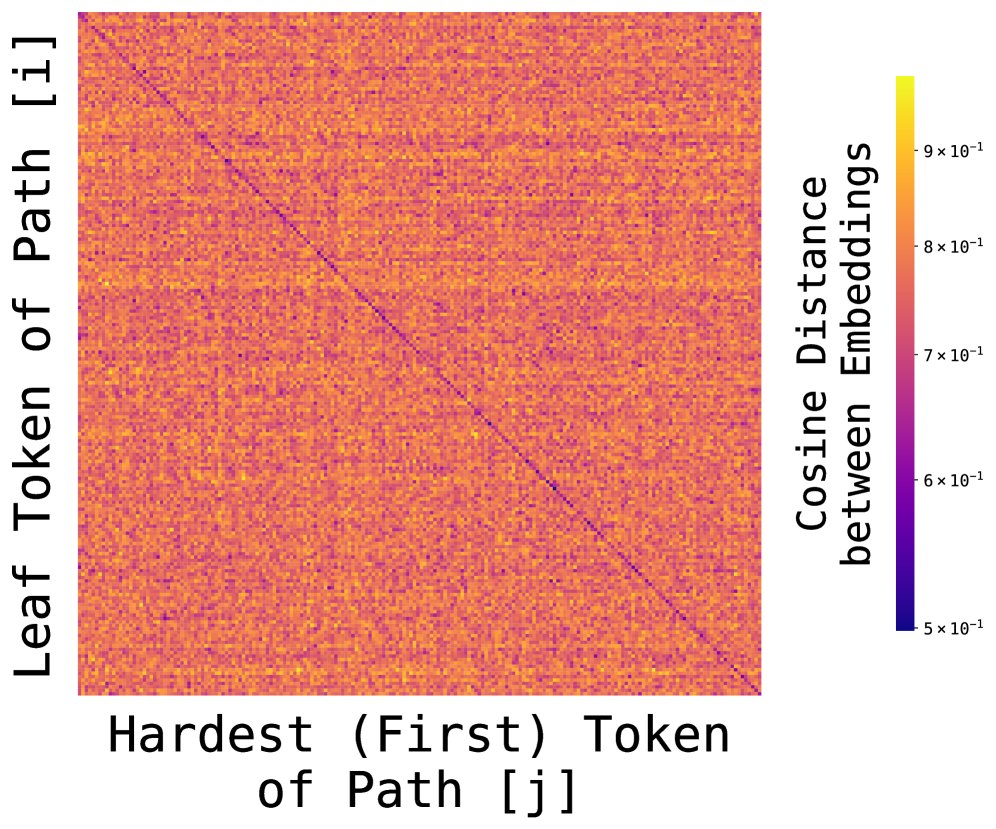Transformer学习到的几何结构 左图：PCA降维后的节点嵌入可视化。不同颜色的点代表不同路径上的节点，可见它们形成了分离的簇。右图：热力图显示了第 i 条路径的叶节点嵌入与第 j 条路径的首跳节点嵌入之间的距离。清晰的对角线表明，同一路径内的节点嵌入更加对齐，反映了全局结构。即使只进行边记忆训练的模型（右下图），也开始呈现出这种几何性。

这个几何式记忆的形成，解释了模型为何能“轻易”解决多步组合推理的难题。因为它从根本上改变了问题的计算复杂度。

悬而未决的问题

尽管几何式记忆的形成解释了模型的成功，但它也带来了更深层次的问题：为什么模型会自发地形成这种优雅而复杂的几何结构？

从优化的角度看，简单的关联式记忆足以让模型在训练集上达到零错误。几何式记忆在参数效率上并不一定更优越。因此，传统的模型容量、优化压力或监督信号都无法直接解释为何模型会“舍近求远”，选择构建一个全局几何结构。本文将此归因于一种尚不明确的谱偏置（spectral bias），并指出这是一个关于深度序列模型记忆机制的根本性开放问题。

实验结论