普特南118分超人类!DeepSeekMath-V2:AI如何学会“自我审日志”?

AI在数学竞赛中再次技惊四座!这一次,DeepSeek-AI推出的DeepSeekMath-V2在顶级的大学生数学竞赛普特南(Putnam)2024中取得了118/120的近乎满分的成绩,远超人类最高分90分。
ArXiv URL:http://arxiv.org/abs/2511.22570v1
更令人瞩目的是,它还在IMO 2025和CMO 2024这两个顶尖高中数学竞赛中达到了金牌水平。
这背后究竟隐藏着怎样的技术突破?答案并非简单的模型堆砌或数据灌输,而是一种全新的范式:自验证数学推理(Self-Verifiable Mathematical Reasoning)。
告别“唯结果论”:从答案到过程的范式转变
过去,训练数学大模型(LLM)的主流方法是奖励最终答案的正确性。模型答对了,就给奖励;答错了,就给惩罚。
这种方法简单粗暴,在一些计算题上效果显著。
但它存在两个致命缺陷:
-
正确答案 ≠ 正确推理:模型可能因为逻辑错误或纯粹的运气猜对答案。这种“知其然不知其所以然”的能力,在严肃的科学研究中毫无用处。
-
无法处理证明题:对于定理证明这类没有数值答案、强调严谨推导过程的任务,最终答案奖励机制完全失效。
结果就是,即使模型能刷榜计算题,其生成的证明过程也常常漏洞百出。要推动AI进行更深层次的推理,就必须教会它不仅要得到答案,更要保证过程的严谨和完备。
DeepSeekMath-V2的核心:三位一体的自验证循环
为了解决这一难题,DeepSeekMath-V2引入了一套精巧的、由生成器和验证器协同工作的训练体系。其核心是一个能够自我迭代、自我完善的闭环。
1. 训练一个“火眼金睛”的证明验证器
研究团队首先训练了一个强大的验证器(Verifier)模型 $\pi_{\varphi}$。
它的任务就像一位数学专家,负责审阅一个证明过程,并根据其完整性、严谨性给出评分(1分:完全正确;0.5分:逻辑正确但有小瑕疵;0分:存在致命错误)。
这个验证器通过强化学习(RL)在大量人工标注的数据上进行训练,学会了如何评判一个证明的质量。
2. 引入“元验证器”确保忠诚度
但问题随之而来:验证器会不会“耍小聪明”?
比如,为了给一个有缺陷的证明打低分,它可能会“凭空捏造”一些不存在的错误来敷衍了事。这种不忠诚(unfaithful)的验证是不可靠的。
为了解决这个问题,研究引入了一个更绝的角色:元验证器(Meta-Verifier)。
它的唯一职责就是审查验证器的“审稿意见”是否合理、是否忠于原文。
通过元验证器的反馈,验证器的奖励函数 $R_{V}$ 变得更加完善,它不仅要预测对分数,还要保证找出的问题是真实存在的。
\[R_{V}=R\_{\text{format}}\cdot R\_{\text{score}}\cdot R\_{\text{meta}}\]引入元验证器后,验证器分析报告的质量分从0.85提升到了0.96,确保了验证的“忠诚度”。
3. 训练一个“自我批判”的证明生成器
有了可靠的验证器作为“裁判”,接下来就是训练证明生成器(Proof Generator)$\pi_{\theta}$。
生成器的目标很简单:生成能从验证器那里获得最高分的证明。
更关键的是,研究团队让生成器学会了“自我批判”。在最终输出答案前,生成器会像验证器一样,反复审视和修改自己的证明,直到找不出任何问题为止。
这个过程被称为通过自验证增强推理(Enhancing Reasoning via Self-Verification)。模型不再是盲目地试错,而是有意识地通过审视和迭代来提升证明质量。
飞轮效应:验证与生成的协同进化
DeepSeekMath-V2最精妙的设计在于,验证器和生成器构成了一个强大的协同进化系统,形成了一个“飞轮效应”。
-
优秀的验证器指导生成器产出更高质量的证明。
-
更强的生成器会产出更复杂、更具挑战性的新证明。
-
这些“难题”反过来成为训练验证器的绝佳新数据,让验证器也变得更强。
-
升级后的验证器又可以更好地指导生成器。
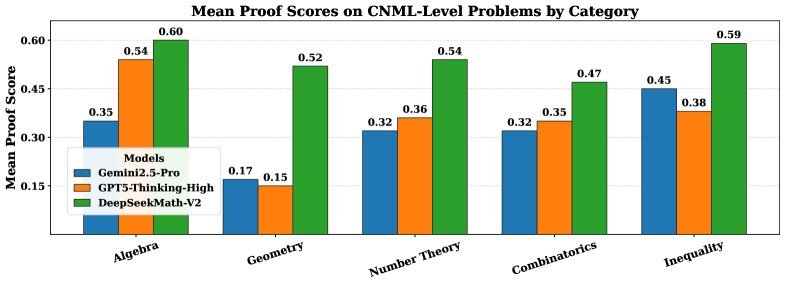
图1:DeepSeekMath-V2在各类问题上均优于其他模型
这个循环一旦启动,就可以在很大程度上实现自动化。在训练的后期迭代中,该流程完全取代了人工标注,实现了可持续的自我提升。
惊人的竞赛表现
理论的先进性最终要靠实践来检验。DeepSeekMath-V2在多个顶级数学竞赛基准上展现了统治级的实力。
研究团队采用了高算力搜索(High-Compute Search)策略,即生成大量候选证明,然后用验证器进行打分,选出最优解。
结果令人震撼:
| 竞赛 | 题目 | 解决情况 | 分数 | 级别 |
|---|---|---|---|---|
| IMO 2025 | 6 | 解决5题 | - | 金牌 |
| CMO 2024 | 6 | 解决4题,1题部分分 | - | 金牌 |
| Putnam 2024 | 12 | 解决11题,1题小错 | 118/120 | 远超人类最高分(90) |
表格1:DeepSeekMath-V2在顶级竞赛中的表现摘要
在与DeepMind的DeepThink(同样达到IMO金牌水平)等模型的对比中,DeepSeekMath-V2也表现出色。
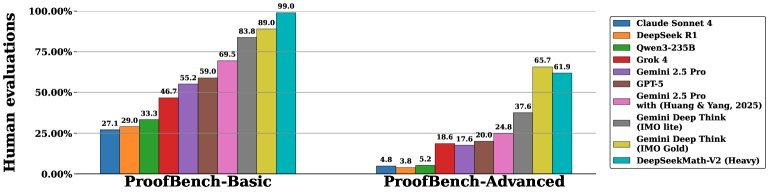
图3:在IMO-ProofBench上的专家评估结果,DeepSeekMath-V2表现优异
值得注意的是,对于那些未能完全解决的难题,模型通常能准确地识别出自己证明中的缺陷。而对于已解决的题目,则能通过所有验证检查。
这证明了模型不仅“能做对”,还“知道自己为什么做对”,真正实现了可靠的自我评估。
总结
DeepSeekMath-V2的成功,标志着AI数学推理从追求“答案正确”迈向了追求“过程可靠”的新阶段。
通过构建验证器、元验证器和生成器的协同进化系统,该研究开创了一条通往自验证AI(Self-Verifiable AI)的可行路径。这种让模型学会“自我审视”和“自我批判”的能力,对于未来构建能够解决科研级别数学难题、甚至推动科学发现的AI系统,具有里程碑式的意义。