Defeating the Training-Inference Mismatch via FP16
-
ArXiv URL: http://arxiv.org/abs/2510.26788v1
-
作者: Zichen Liu; Xiangxin Zhou; Penghui Qi; Chao Du; Tianyu Pang; Min Lin; Wee Sun Lee
-
发布机构: National University of Singapore; Sea AI Lab
TL;DR
本文发现,在强化学习微调大型语言模型时,仅需将训练精度从广泛使用的 BF16 切换回 FP16,即可从根源上解决训练与推理策略之间的数值不匹配问题,从而获得更稳定的优化、更快的收敛和更强的模型性能。
关键定义
- 训练-推理不匹配 (Training-Inference Mismatch): 在现代强化学习(RL)框架中,为了效率,通常会使用不同的计算引擎进行训练(梯度计算)和推理(rollout/采样)。尽管两者在数学上等价,但由于浮点精度误差和硬件特定的优化,它们会产生数值上不同的输出。这种策略上的微小差异被称为“训练-推理不匹配”,它会导致梯度有偏和部署性能下降等问题。
- BF16 (BFloat16): 一种16位浮点数格式,分配8位给指数部分和7位给尾数部分。它的动态范围与32位浮点数(FP32)相同,能有效避免梯度上溢或下溢,因此在大型模型预训练中被广泛采用以保证稳定性。然而,其较低的精度(尾数位数少)使其容易产生舍入误差。
- FP16 (Float16): 一种16位浮点数格式,分配5位给指数部分和10位给尾数部分。相较于BF16,它的动态范围较小,容易出现上溢和下溢问题,但其更高的精度(尾数位数多)使得数值计算结果更加精确。
- 损失缩放 (Loss Scaling): 一种用于稳定FP16训练的技术。通过在反向传播前将损失乘以一个大的缩放因子 \(S\),可以将微小的梯度值放大到FP16可表示的范围内,避免因下溢而丢失信息。在权重更新前,再将梯度除以 \(S\) 恢复原样。
相关工作
当前,通过强化学习微调大型语言模型(LLMs)以提升推理性能是一种前沿方法,但其训练过程极不稳定,经常面临训练崩溃的风险。一个关键的瓶颈是训练-推理不匹配问题:用于快速采样的推理引擎和用于梯度计算的训练引擎在数值上存在差异,即使它们加载的是同一套模型参数。
为解决此问题,先前的工作主要分为两类:
- 算法修正:通过重要性采样(Importance Sampling, IS)来修正有偏的梯度。例如,Yao et al. (2025) 提出了Token级别的截断重要性采样(Truncated Importance Sampling, TIS)作为补丁,但其梯度仍有偏。Liu et al. (2025a) 提出了序列级别的掩码重要性采样(Masked Importance Sampling, MIS),虽然无偏,但收敛速度慢。这些方法不仅增加了约25%的额外计算开销(需要一次额外的前向传播),而且无法解决“部署差距”——即模型参数是针对训练引擎优化的,而非部署时使用的推理引擎。
- 工程对齐:尝试从工程实现上统一训练和推理的行为。例如,手动对齐底层实现或强制确定性推理。但这类方法需要深厚的领域知识,工程量巨大,且难以跨框架或模型泛化。
本文旨在从根源上解决训练-推理不匹配问题,而不是通过复杂的算法或脆弱的工程手段进行弥补。
本文方法
本文的核心论点是,训练-推理不匹配的根源在于数值精度本身,特别是广泛使用的 BF16 格式。作者提出一个极其简单的解决方案:在RL微调阶段,将训练精度从 BF16 切换回 FP16。
创新点
本文的创新之处在于,它没有设计新的复杂算法,而是回归问题的本源,识别出浮点数精度是导致策略不匹配的关键因素。
BF16 拥有与 FP32 相同的动态范围(8位指数),但牺牲了精度(7位尾数)。这使其在预训练中非常稳定,能避免梯度消失或爆炸。然而,在RL微调中,正是这种低精度导致了问题:训练和推理引擎中不同的计算实现(如CUDA内核优化、并行策略差异)会产生不同的舍入误差,这些误差在自回归生成过程中不断累积,最终导致两个引擎输出的概率分布 \($\operatorname\*{{\color[rgb]{0,0,1}\pi}}\)$ (训练) 和 \($\operatorname\*{{\color[rgb]{1,0,0}\mu}}\)$ (推理) 显著偏离。
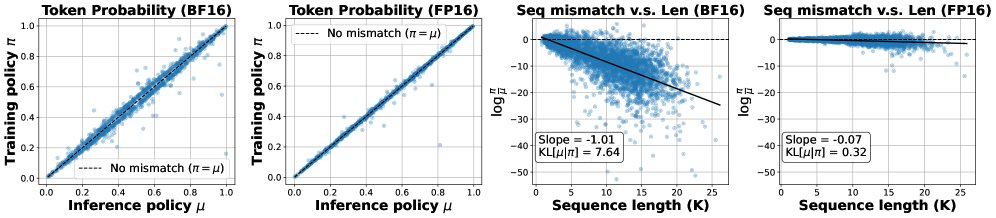
上图的离线分析直观地展示了这一点。左侧两图显示,相比于BF16,FP16下训练和推理引擎计算的Token概率分布更紧密地聚集在对角线附近,表明不匹配程度更低。右侧两图显示,随着生成序列变长,BF16下序列级别的对数概率比率(\($\log(\pi/\mu)\)$)的偏差会急剧增大,而FP16则能将偏差维持在非常小的水平。
优点
切换到 FP16 的核心优势在于其更高的精度。FP16 拥有10位尾数,其精度是 BF16 的 $2^3=8$ 倍。
| FP16 | BF16 | |
|---|---|---|
| 指数位 (Exponent Bits) | 5 | 8 |
| 尾数位 (Mantissa Bits) | 10 | 7 |
| 最小正规数 | $\approx 6.1\times 10^{\mathbf{-5}}$ | $\approx 1.2\times 10^{\mathbf{-38}}$ |
| 最大值 | $\approx 6.6\times 10^{\mathbf{4}}$ | $\approx 3.4\times 10^{\mathbf{38}}$ |
| 大于1的下一个可表示数 | $1+2^{\mathbf{-10}}\approx 1.000977$ | $1+2^{\mathbf{-7}}\approx 1.007812$ |
这种高精度使得计算结果对底层实现差异的敏感度大大降低,有效抑制了舍入误差的累积,从而从根本上消除了策略不匹配。
对于RL微调而言,模型的权重和激活值的动态范围已在预训练阶段确定,BF16的超大动态范围并非必需,反而其牺牲的精度成为了主要短板。而FP16虽然动态范围小,但可以通过成熟的损失缩放技术有效解决梯度下溢问题。在PyTorch等现代框架中,启用动态损失缩放仅需几行代码,非常便捷。
总结而言,该方法的优点包括:
- 根本性解决:直接消除不匹配的根源,而非事后补偿。
- 简单高效:无需修改模型架构或RL算法,仅需更改数据类型配置,并避免了额外计算开销。
- 解决部署差距:由于训练和推理策略高度一致,优化后的模型在部署时能表现出更佳的性能。
实验结论
本文引入了一个“理智检查测试(Sanity Test)”来评估RL算法的可靠性。该测试构建了一个“可完美解决的数据集”,其中所有问题都已知模型有能力解决(初始准确率在20%-80%之间),但并非轻而易举。一个可靠的算法应该能在这个数据集上达到近乎100%的准确率。
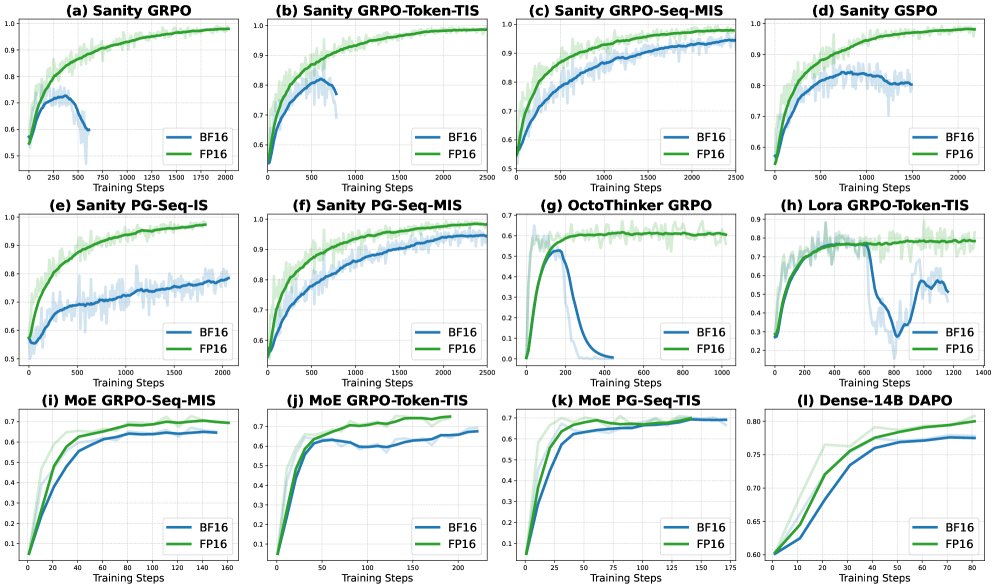
上图展示了在多种实验设置下,FP16相比BF16的训练奖励对比。关键结论如下:
- 普遍有效性:无论是在本文设计的理智检查测试上,还是在不同的RL算法(如GRPO, GSPO, TIS, MIS, PG)、不同的模型家族(R1D, Qwen)、不同的微调方法,以及更大规模的模型上,使用FP16(实线)进行训练均一致地获得了比BF16(虚线)更高且更稳定的训练奖励。
- 框架无关性:这一优势在两个独立的RL框架(VeRL和Oat)中都得到了验证,证明了该方法的普适性。
离线分析也表明,尽管FP16在推理精度上本身不一定带来直接性能提升(如下表所示),但它通过减小训练-推理不匹配(偏差减小约24倍),为RL优化过程创造了更稳定、更一致的环境。
DeepSeek-R1-Distill-Qwen-1.5B模型在不同精度下的离线评估分数
| dtype | AMC23 (8K) | AIME24 (8K) | AMC23 (32K) | AIME24 (32K) |
|---|---|---|---|---|
| BF16 | 50.38 | 22.60 | 62.35 | 29.90 |
| FP16 | 50.60 | 20.10 | 63.10 | 30.94 |
| FP32 | 51.54 | 22.30 | 62.42 | 28.44 |
最终结论是,在RL微调LLM的场景下,简单地从BF16切换到FP16是一个纯粹的胜利:它以极小的实现成本,换来了更稳定的优化、更快的收敛和更强的最终性能,有效解决了长期困扰该领域的训练不稳定性问题。