Do Not Step Into the Same River Twice: Learning to Reason from Trial and Error

• ArXiv URL: http://arxiv.org/abs/2510.26109v1

• 作者: Yunfang Wu; Saiyong Yang; Chenming Tang; Hsiu-Yuan Huang; Weijie Liu

• 发布机构: Peking University; Tencent

---

TL;DR

本文提出了一种名为 LTE（Learning to reason from Trial and Error） 的方法，通过利用大语言模型（LLM）自身在推理失败时产生的错误答案作为提示信息，来克服强化学习中的探索停滞问题，从而无需任何外部专家指导即可提升模型的推理能力。

关键定义

• 可验证奖励的强化学习 (Reinforcement Learning with Verifiable Rewards, RLVR)：一种面向大语言模型后训练的新兴强化学习范式。在该框架下，模型响应的正确性可以被自动、客观地验证，从而自动给予奖励信号，特别适用于数学推理等任务。
• 探索停滞 (Exploration Stagnation)：现有 RLVR 方法的一个核心瓶颈。当模型对于某个难题的所有尝试（rollouts）都失败时，它收到的奖励均为零，导致梯度也为零，从而无法从该样本中学习，其能力被自身的初始水平所限制，无法攻克更难的问题。
• LTE (Learning to reason from Trial and Error)：本文提出的核心方法。它旨在解决探索停滞问题。对于模型完全无法解决的难题（即所有尝试都失败的样本），LTE 会收集这些失败尝试中产生的错误答案，并将这些错误答案作为“提示”信息融入到新的输入中，引导模型进行额外的尝试，从而提高找到正确解的概率。

相关工作

目前，利用可验证奖励的强化学习（RLVR）是提升大语言模型（LLM）推理能力的主流技术。然而，现有的 RLVR 方法大多依赖模型自身的策略进行探索（on-policy），这导致了一个严重的瓶颈：探索停滞。具体来说，如果一个训练问题超出了模型当前的能力上限，模型的所有尝试都会失败，从而获得零奖励。在这种情况下，如 GRPO 等标准优化算法的梯度会变为零，模型无法从这些高难度的失败样本中获得任何有效的学习信号，其能力提升因此陷入停滞。

为了打破这一瓶颈，一些研究工作尝试引入外部指导，例如使用人类标注的正确解题步骤或更强模型的输出。但这些方法要么成本高昂、难以扩展，要么在训练顶级模型时（不存在更强的模型）不可行。

本文旨在解决上述探索停滞问题，但其核心目标是在不依赖任何外部专家（无论是人类还是更强的模型）指导的情况下，仅凭模型自身的“试错”经验来突破能力上限。

本文方法

本文提出的 LTE (Learning to reason from Trial and Error) 框架旨在利用模型自身的失败经验来克服探索停滞。其核心思想是：当模型对一个问题的所有尝试都失败时，不应白白浪费这些计算，而应从中提取信息，以指导后续的探索。

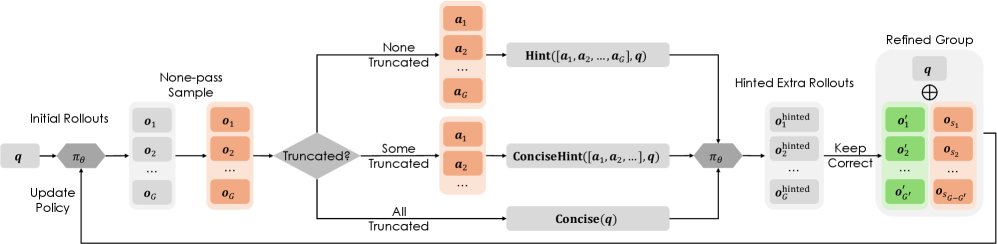对于所有尝试都失败的样本，LTE 会提取模型生成的错误答案作为提示，用于额外的 rollouts。为简洁起见，图中省略了其他类型的样本。

创新点：带提示的额外探索 (Hinted Extra Rollouts)

与简单地增加尝试次数（vanilla extra rollouts）不同，LTE 根据失败的具体原因生成特定的提示，进行更有针对性的额外探索。

1. 识别“探索停滞”样本：对于一个给定的问题，首先让模型生成 $G$ 次响应（rollouts）。如果所有 $G$ 次响应都未能通过验证（即奖励全为0），则该样本被标记为“停滞样本”。

2. 生成提示：根据失败的模式，生成不同类型的提示：

   • 冗长失败 (Overlong Failure)：如果所有失败的响应都因为过长而被截断，模型可能陷入了冗长无效的思考。此时，向模型提供一个简单的提示，让它“简明扼要地思考”。
   • 答案错误 (Incorrect Answer Failure)：如果存在未被截断的失败响应，系统会从中提取出所有错误的答案。这些答案反映了模型容易犯的错误。接着，将这些错误答案整合进提示中，要求模型在新的尝试中不要再次生成这些答案，从而缩小搜索空间，避免“在同一条河里跌倒两次”。

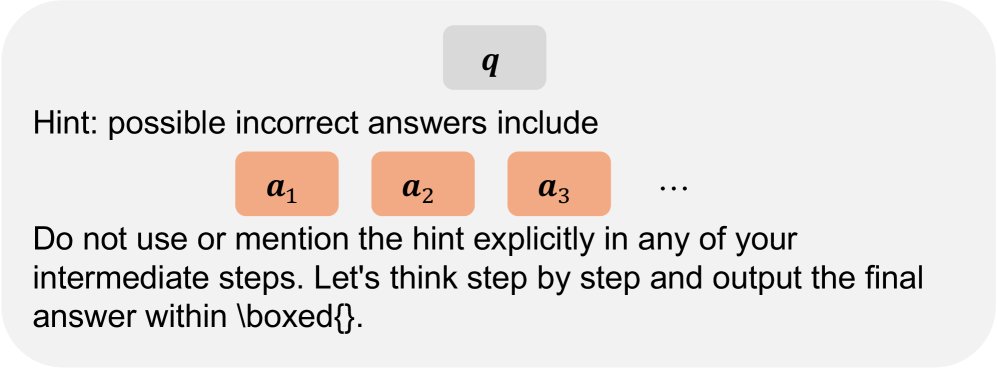
   下图展示了不同场景下使用的提示模板：

正常提示模板 $\textbf{Prompt}(\cdot)$	\(overlong-all\) 样本提示模板 $\textbf{Concise}(\cdot)$
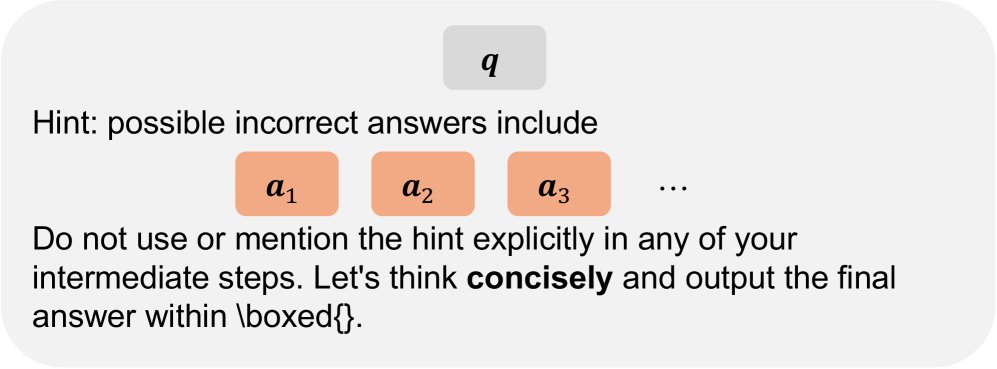\(overlong-some\) 样本提示模板 $\textbf{ConciseHint}(\cdot)$	\(pass-none\) 样本提示模板 $\textbf{Hint}(\cdot)$

1. 执行额外探索：使用包含上述提示的新 prompt，模型再进行 $G$ 次额外的探索。

核心机制：混合策略优化 (Mixed-policy Optimization)

通过带提示的额外探索，模型现在有更大概率获得正确的解。然而，这些正确解是在“提示”这个额外条件下生成的，属于离策略 (off-policy)数据，不能直接用于优化原始策略（即在没有提示下解决问题的策略）。

为了解决这个问题，LTE 采用了一种混合策略优化方法：

• 如果额外的探索产生了 $G’$ 个正确解，就用这些正确解随机替换掉原始的 $G’$ 个失败解。
• 在更新模型时，对这些离策略的正确解采用正则化的重要性采样 (regularized importance sampling)进行处理，以修正其对策略梯度的贡献。其目标函数结合了离策略和在策略的样本进行更新：

\[\mathcal{J}_{\text{Mixed}}(\theta)= \mathbb{E}_{q,\{o'_{i},o_{s_{i}}\}}\Bigl[\frac{1}{Z'}\sum_{i=1}^{G'}\sum_{t=1}^{ \mid o'_{i} \mid }(f(\hat{r}'_{i,t}(\theta))\cdot\hat{A}'_{i,t}) +\frac{1}{Z}\sum_{i=1}^{G-G'}\sum_{t=1}^{ \mid o_{s_{i}} \mid }\Bigl(\operatorname{CLIP}(r_{s_{i},t}(\theta),\hat{A}_{s_{i},t},\varepsilon\Bigr)\Bigr]\]

其中，$f(\hat{r}’_{i,t}(\theta))$ 是对离策略样本的重要性采样比率 $\hat{r}’_{i,t}(\theta)$ 进行正则化的函数。通过这种方式，模型能够安全地从这些来之不易的正确解中学习，同时保持对原始任务的优化。

以下是 LTE 的完整训练流程伪代码： ``$$ Algorithm 1: Learning from Trial and Error (LTE)

Input: 策略模型 π_θ, rollout数量 G, 批大小 n, 训练步数 T, 训练数据 D Output: 更新后的策略模型 π_θ

for t = 1 to T do:

1. 从 D 中采样一批问题 Q
2. for 每个问题 q in Q do: a. 初始探索：用 π_θ 生成 G 个响应 O_q b. 验证与评估：检查 O_q 中每个响应的正确性，得到奖励 R_q c. if 所有奖励均为 0 (探索停滞) then: i. 根据失败类型（是否全为超长响应）生成提示 q’ ii. 额外探索：用提示 q’ 和 π_θ 生成 G 个新响应 O_hinted_q iii. 验证新响应，找出其中的正确解 O_q iv. 用正确解 O_q 替换 O_q 中的部分失败解 d. 计算最终响应组的优势函数 Â
3. 执行混合策略更新：使用所有问题的响应 O 和优势 Â 更新 π_θ return π_θ \(`\)

优点

• 自给自足：完全不依赖外部专家知识（如人工标注或更强模型），仅利用模型自身的计算和失败经验，通用性强且成本低。
• 信息利用高效：将失败的探索从“无用功”转化为有价值的“负向指导”，比简单增加探索次数更有效率。
• 兼顾探索与利用：不仅解决了难题，提高了模型的利用能力（exploitation），实验还证明它能提升模型的探索上界（exploration）。

实验结论

本文在 Qwen3-4B-Base 和 Qwen3-8B-Base 模型上，针对六个数学推理基准进行了实验。

核心结果

• 性能全面超越基线：在 Pass@1（衡量利用能力）和 Pass@k（衡量探索能力）指标上，LTE 方法均显著优于标准的 GRPO 以及简单增加探索次数的基线方法。在 Qwen3-4B-Base 模型上，LTE 平均将 Pass@1 提高了 6.38%，Pass@k 提高了 9.00%。

  Qwen3-4B-Base Pass@1 (%) 结果

  方法	MATH-500	Minerva	OlympiadBench	AMC’23	AIME’24	AIME’25	平均
  无 Entropy Loss
  Base Model	45.40	19.49	22.81	35.31	8.75	3.75	22.59
  GRPO	69.65	32.17	34.33	50.62	12.08	4.38	33.87
  GRPO + Extra Rollouts	69.30	31.99	35.59	55.78	11.88	6.46	35.17
  LTE (本文方法)	70.60	33.30	35.70	55.94	17.29	10.63	37.24
  有 Entropy Loss
  GRPO	73.25	30.15	38.44	55.00	18.96	13.96	38.29
  GRPO + Extra Rollouts	69.75	33.46	34.52	54.84	19.17	8.96	36.78
  LTE (本文方法)	76.05	35.70	35.59	57.19	23.96	14.17	40.44

  Qwen3-4B-Base Pass@k (%) 结果

  方法	MATH-500	Minerva	OlympiadBench	AMC’23	AIME’24	AIME’25	平均
  无 Entropy Loss
  Base Model	69.80	37.87	39.70	82.50	33.33	26.67	48.31
  GRPO	77.20	37.50	42.07	75.00	26.67	26.67	47.52
  GRPO + Extra Rollouts	76.00	38.60	44.30	80.00	26.67	20.00	47.60
  LTE (本文方法)	81.00	39.46	45.47	80.00	36.67	23.33	50.99
  有 Entropy Loss
  GRPO	81.80	39.34	47.11	77.50	46.67	33.33	54.29
  GRPO + Extra Rollouts	77.80	40.44	41.93	85.00	40.00	26.67	51.97
  LTE (本文方法)	83.60	43.75	45.74	85.00	50.00	36.67	57.46

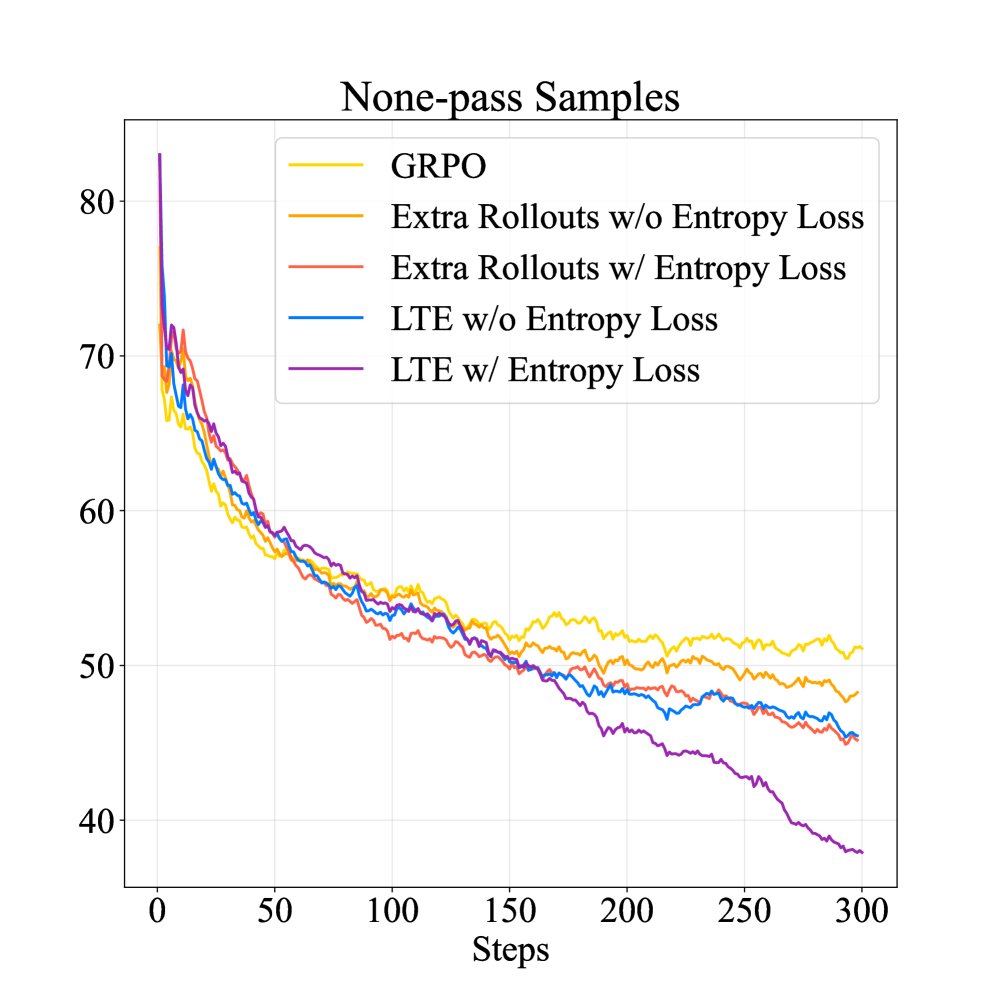
• 有效缓解探索停滞：训练过程分析表明，标准 GRPO 方法在训练后期无法解决更多难题（\(all-fail\) 样本数量不再下降），而 LTE 能持续降低 \(all-fail\) 样本的数量，直接证明其成功缓解了探索停滞问题。

• 提升探索与学习效率：LTE 在训练中保持了较高比例的“可学习样本”（\(some-pass\) 样本，即有成功也有失败的样本，提供最有效的学习信号），同时降低了“过度自信样本”（$$all-pass` 样本）的比例。这表明 LTE 维持了更高的探索水平，避免了过早收敛。

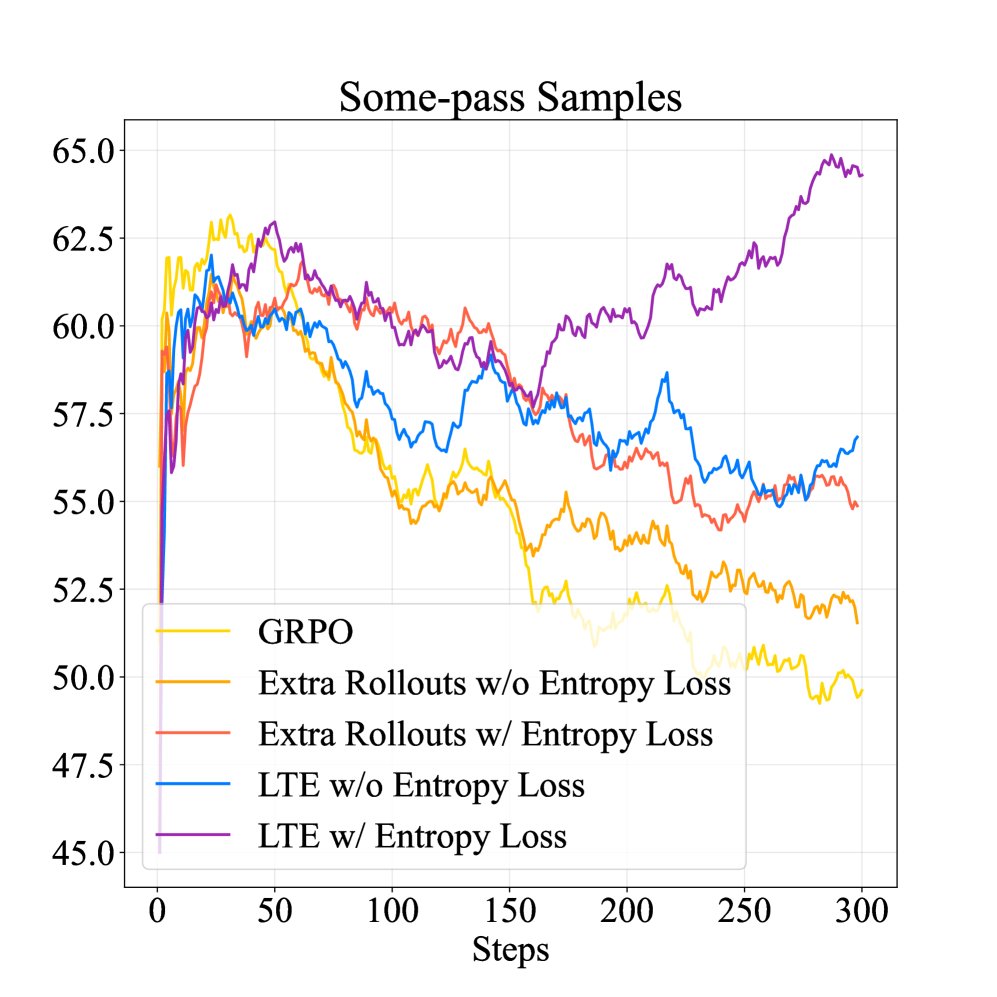
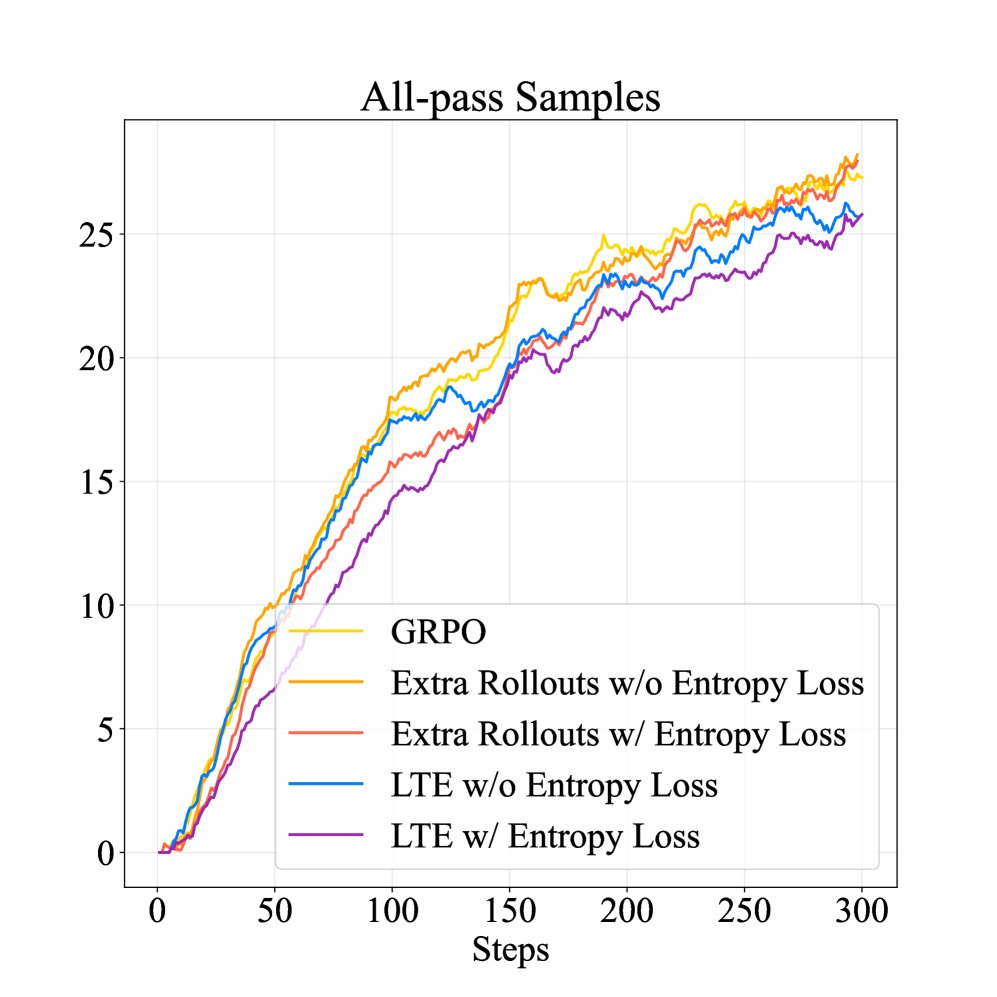
• 激发深度思考与探索：训练动态分析显示，相比于基线方法，LTE 不仅在验证集上取得了持续的性能提升，还显著增加了模型生成答案的长度。这表明 LTE 隐式地鼓励了模型进行更深入的“测试时深度思考”（test-time deep thinking），花费更多 token 进行探索，最终形成了一个更具探索性的策略。

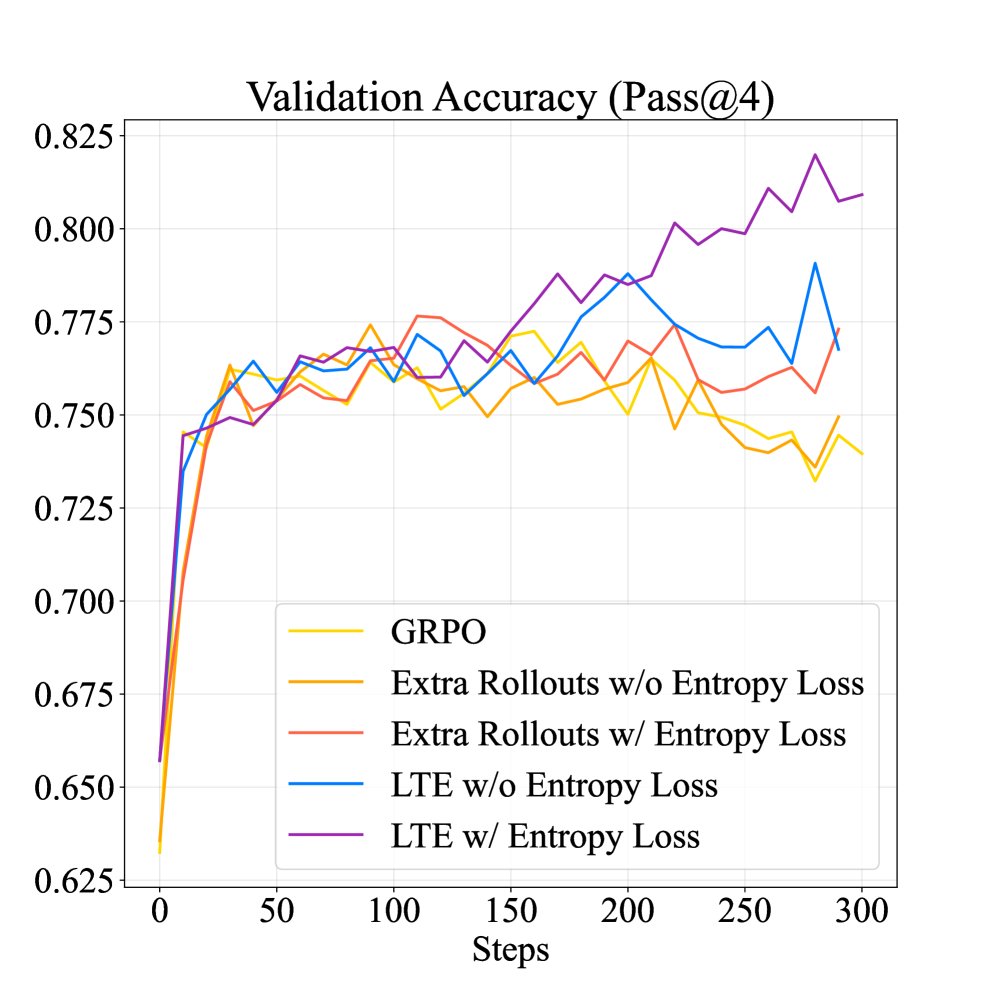
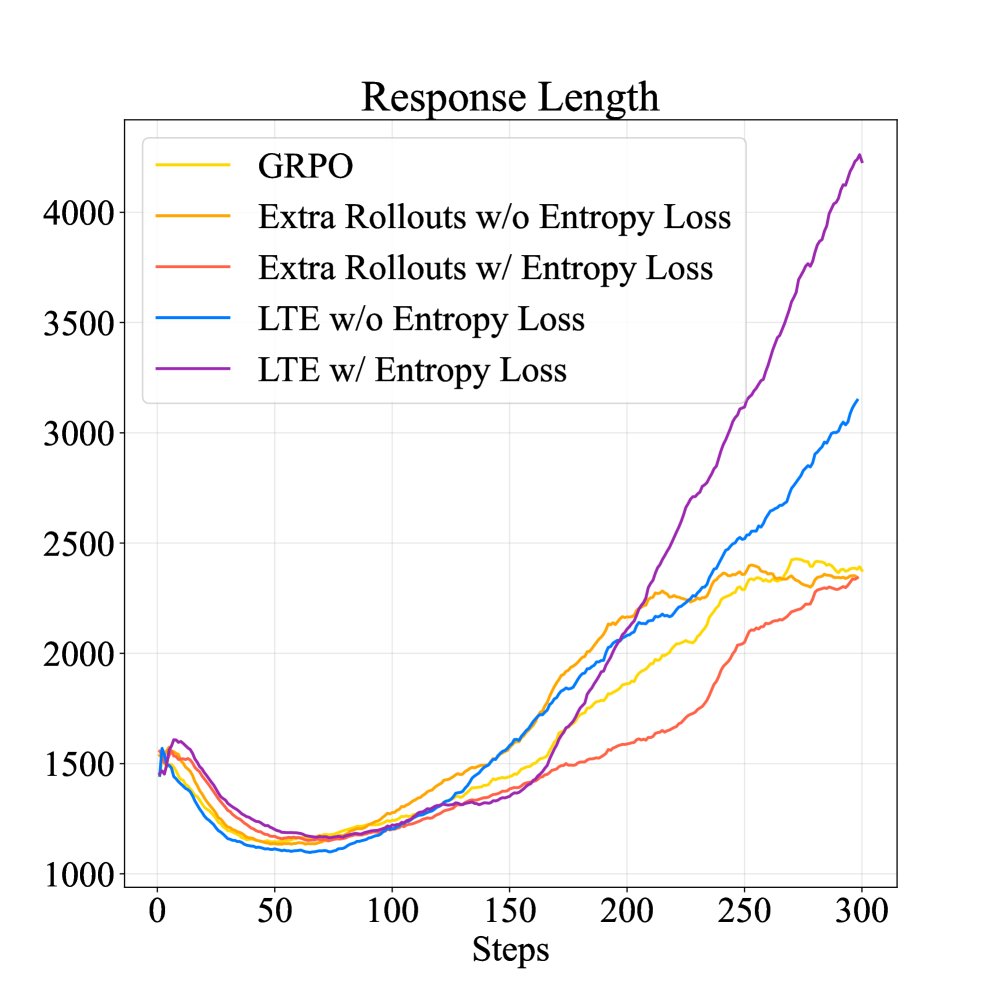
结论

实验结果有力地证明，LTE 方法通过利用模型自身的试错经验，成功地解决了 RLVR 中的探索停滞问题。它在不依赖任何外部专家指导的前提下，同时提升了模型的利用（exploitation）和探索（exploration）能力，为提升大语言模型推理能力提供了一条有效、通用且高效的路径。