AMD力作Dual LoRA：性能最高提升1.8%！将参数更新分解为“幅值”与“方向”

大模型微调技术LoRA已经无处不在，但你是否想过，它为何总是与全量微调（FFT）存在性能差距？现在，来自AMD的研究团队给出了一个全新的答案，并带来了一个优雅而强大的解决方案——Dual LoRA。

ArXiv URL：http://arxiv.org/abs/2512.03402v1

这项研究不搞复杂的结构，而是回归本源，通过一个简单的“拆分”思想，让LoRA的性能在同等参数量下稳定超越了DoRA等一众SOTA变体，在部分任务上甚至取得了高达1.8%的性能提升！

首先，我们快速回顾一下参数高效微调（Parameter-Efficient Fine-Tuning, PEFT）领域的明星——LoRA。

它的核心假设是：模型在适应下游任务时，参数的改变量是“低秩”的。因此，它冻结原始权重$W_0$，并通过训练两个低秩矩阵$A$和$B$来学习一个更新矩阵$\Delta W = BA$。

这种方法极大地减少了需要训练的参数，但“低秩假设”也成了一把双刃剑。它限制了模型更新的自由度，导致与全量微-调相比，性能常常不尽如人意。

那么，如何突破这一瓶颈？Dual LoRA的思路非常巧妙：模拟全量微调中基于梯度的优化过程。

在梯度下降中，对每个参数的更新都包含两个核心信息：

传统的LoRA用一个$\Delta W$矩阵混合了这两个信息，而Dual LoRA则主张将它们解耦，分开学习！

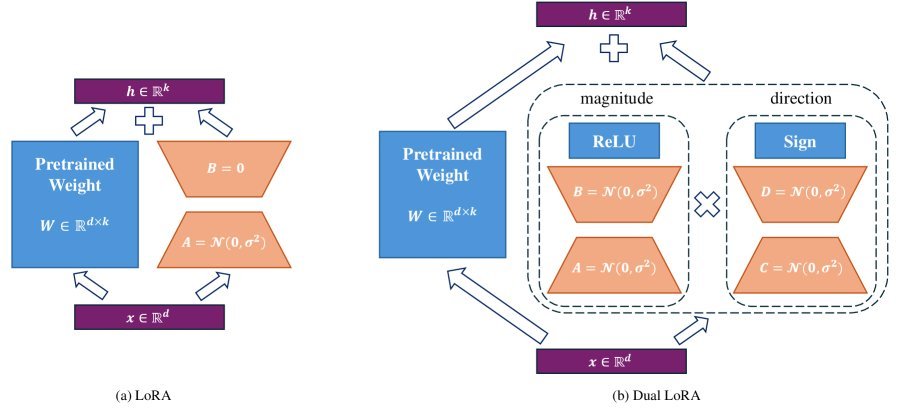
图1：原始LoRA（左）与Dual LoRA（右）的架构对比

如上图所示，Dual LoRA引入了两组、共四个低秩矩阵：

幅值组 (Magnitude Group)：由矩阵$A$和$B$组成，通过$ReLU$激活函数生成幅值矩阵$W_m = \text{ReLU}(BA)$。$ReLU$确保了所有更新幅值都是非负的，这很直观——更新的“力度”没有正负之分。
方向组 (Direction Group)：由矩阵$C$和$D$组成，通过$Sign$函数生成方向矩阵$W_d = \text{Sign}(DC)$。$Sign$函数将输出限制在$+1$或$-1$，清晰地决定了每个参数是“前进”还是“后退”。

最终，总的更新矩阵$\Delta W$通过将幅值和方向进行逐元素相乘（Hadamard Product, $\odot$）得到：

\[\Delta W = \frac{\alpha}{\sqrt{r_1 r_2}} (\text{ReLU}(BA) \odot \text{Sign}(DC))\]

其中$r_1$和$r_2$分别是两组的秩，$\alpha$是缩放因子。

这个设计引入了一个强大的归纳偏置（inductive bias）：模型被引导去分别学习“更新多大幅度”和“朝哪个方向更新”，这比混合学习要更接近优化的本质。

理论上的优雅是否能转化为实际的性能提升？答案是肯定的。

该研究在自然语言生成（NLG）、理解（NLU）和常识推理等多种任务上，对GPT-2、RoBERTa、DeBERTa以及LLaMA-1/2/3系列模型进行了广泛测试。

结果显示，在可训练参数相同或更少的情况下，Dual LoRA全面且稳定地优于LoRA、LoRA+和DoRA等现有SOTA方法。

常识推理任务：在LLaMA-7B/13B模型上，Dual LoRA的平均准确率比之前的最佳结果高出0.9%和0.6%。在LLaMA2-7B和LLaMA3-8B/70B上同样表现出色。
NLU任务（GLUE基准）：在RoBERTa-base模型上，Dual LoRA相比LoRA、LoRA+和DoRA分别高出1.6%、1.2%和1.8%！在更大的模型上，优势依然显著。
超越全量微调：更令人惊讶的是，在某些NLU任务上，Dual LoRA的表现甚至超过了全量微调（FFT），这充分证明了其方法的优越性。

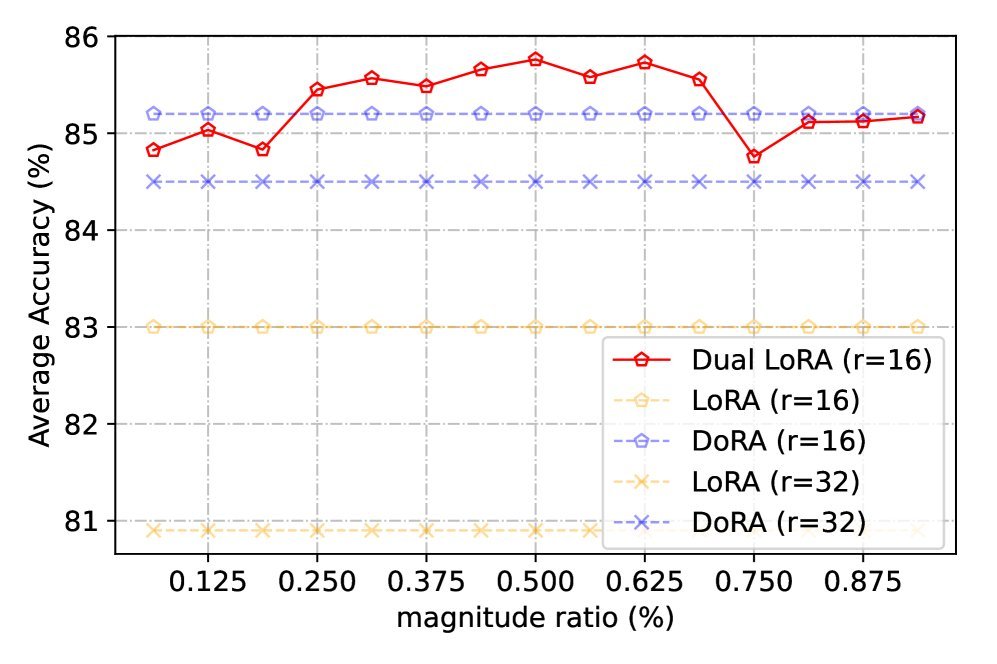
图2：在LLaMA3-8B上的实验，Dual LoRA（红线）在不同秩分配下始终优于DoRA（蓝线）和LoRA（橙线）

Dual LoRA成功的背后，还有一个更深层次的原因：它能实现更高秩的更新。

标准LoRA的更新矩阵$\Delta W = BA$的秩最高只能为$r$。而Dual LoRA的更新矩阵$\Delta W’ = W_m \odot W_d$，其秩理论上可以远超$r_1$和$r_2$。两个矩阵的逐元素积的秩最高可以达到$r_m \times r_d$。

这意味着Dual LoRA有潜力产生一个表达能力更强、更复杂的更新矩阵，从而更接近全量微调的效果。

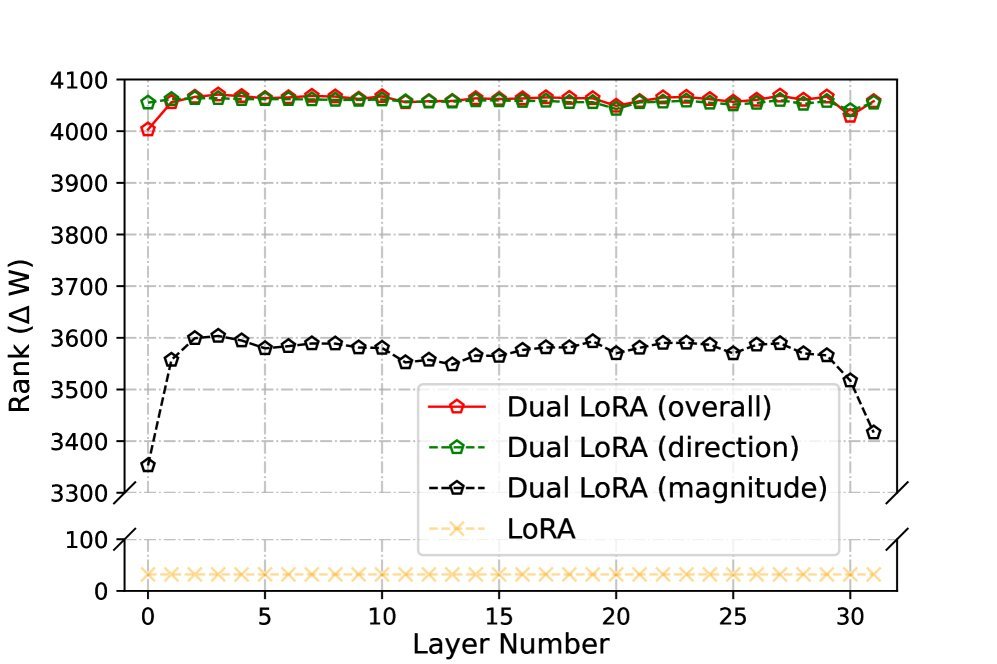
图3：在LLaMA2-7B上不同层的更新矩阵秩。Dual LoRA（绿色）的整体更新秩远高于原始LoRA（蓝色）

上图清晰地展示了这一点。在LLaMA2-7B的实验中，Dual LoRA的最终更新矩阵（绿色）和方向矩阵（红色）几乎达到了满秩（4096），而原始LoRA的更新秩（蓝色）则非常低。这从数学上解释了Dual LoRA为何如此有效。

面对PEFT方法性能普遍不及全量微调的挑战，Dual LoRA没有选择堆叠复杂的模块，而是回归到梯度优化的基本原理。

通过将参数更新解耦为“幅值”和“方向”两个独立部分，Dual LoRA为LoRA框架引入了一个强大且符合直觉的归纳偏置。它不仅在概念上简单优雅，更在大量实验中证明了其SOTA级别的性能。

对于追求更高微调性能的开发者来说，Dual LoRA无疑是一个值得立即尝试的新选择。它再次证明，有时候，最深刻的洞察往往源于对基础原理的重新审视。