Efficient Reinforcement Learning for Large Language Models with Intrinsic Exploration
-
ArXiv URL: http://arxiv.org/abs/2511.00794v1
-
作者: Zihao Wang; Stanley Kok; Jia Guo; Zujie Wen; Yan Sun; Zhiqiang Zhang
-
发布机构: Ant Group; National University of Singapore
TL;DR
本文提出了一种名为PREPO的高效强化学习方法,通过结合基于提示困惑度(Perplexity)的课程学习调度和基于相对熵(Relative Entropy)的探索性序列加权,在不牺牲模型性能的前提下,将大语言模型在强化学习训练中的数据效率提升了高达3倍。
关键定义
- 带可验证奖励的强化学习 (Reinforcement Learning with Verifiable Rewards, RLVR):一种强化学习范式,用于提升大语言模型的推理能力。模型通过生成多个解题路径(rollouts),并根据是否有可验证的正确答案(如数学题的最终结果)来获得奖励,从而优化自身策略。
- 困惑度调度在线批选择 (PPL-Schedule Online Batch Selection):本文提出的提示(prompt)选择策略。它利用提示的困惑度(Perplexity)作为模型对其理解程度的代理指标,通过一个预设的调度机制,使模型在训练初期专注于“简单”(低困惑度)的提示,然后逐渐过渡到“困难”(高困惑度)的提示,实现一种无监督的课程学习。
- 相对熵加权 (Relative-Entropy Weighting):本文提出的对生成序列(rollout)进行加权的策略。它计算每个序列的平均熵,并将其与当前批次内所有序列的平均熵进行比较,得出一个相对权重。该权重会放大那些不确定性更高、更具探索性的序列在训练中的影响,从而在优化过程中保持探索性。
- PREPO (Perplexity-Schedule with Relative-Entropy Policy Optimization):本文提出的核心方法,是上述两种策略的结合。它在RLVR训练流程中,首先通过PPL调度选择信息量大的提示,然后在策略优化时,通过相对熵加权来优先学习那些探索性强的生成序列。
相关工作
当前,通过带可验证奖励的强化学习(RLVR)来优化模型自生成的解题路径,已成为提升大语言模型(LLM)推理能力的主流方法。然而,RLVR的训练成本极高,其主要瓶颈在于生成rollout的过程非常耗时。
一个关键的低效来源是并非所有训练样本都对模型优化有同等贡献。在提示(prompt)层面,一些问题对于当前模型来说可能过于简单或过于困难,无法产生有效的学习梯度。在生成序列(rollout)层面,即使答案正确,模型生成的路径也存在置信度差异;高置信度(低熵)的回答产生的梯度较小,而高不确定性(高熵)的回答则可能揭示了多样的推理路径,更有利于探索。
现有方法尝试通过参数化模型、重放缓冲区或选择性执行rollout来解决数据效率问题。本文从一个新的角度出发,旨在解决以下具体问题:如何利用数据内在的、几乎无计算开销的属性(如文本困惑度和生成熵),来智能地筛选训练数据,从而在保证甚至提升模型性能的同时,大幅降低RLVR的训练成本?
本文方法
本文提出了PREPO (Perplexity-Schedule with Relative-Entropy Policy Optimization),该方法整合了两个互补的组件来提升RLVR的数据效率,其核心是利用数据的内在属性来指导训练过程。
PPL调度在线批选择
该组件旨在实现一种从易到难的课程学习。其基本思想是,一个提示(prompt)对于当前模型的困惑度(PPL)可以作为其难度的动态指标。
-
动态难度衡量:对于一个提示 $x_i$,其在训练进度为 $\rho$ 时的困惑度计算如下,其中 $\pi_\rho$ 是当时的模型:
\[P_{i}(\rho)=\exp\left(-\frac{1}{T}\sum_{t=1}^{T}\log\pi_{\rho}(x_{i,t}\mid x_{i},x_{i,<t})\right)\]初步分析表明,提示的PPL与任务的成功率(passrate)呈显著负相关,即低PPL通常对应高成功率。
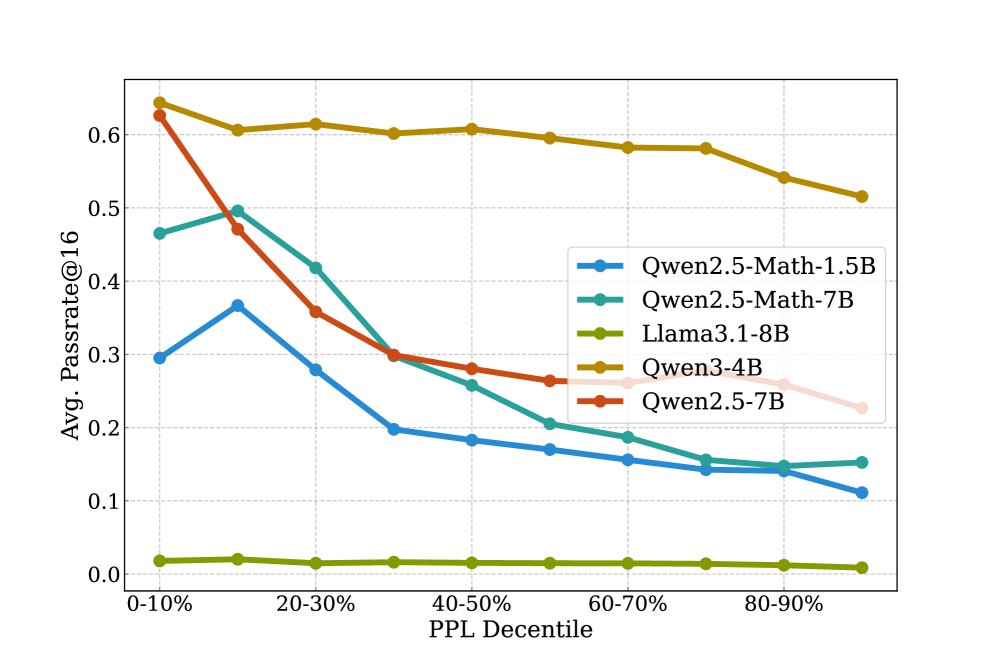
-
调度选择机制:在每个训练批次 $\mathcal{B}$ 中,首先根据所有提示的PPL值 $P_i(\rho)$ 对其进行升序排序。然后,根据当前的训练进度 $\rho \in [0, 1]$,通过一个线性调度函数 $l(\rho)=\big\lfloor\rho\cdot( \mid \mathcal{B} \mid -K)\big\rfloor$ 来确定选择窗口的起始位置,从而选出一个大小为 $K$ 的子批次 $\mathcal{I}_\rho$。
\[\mathcal{I}_{\rho}=\{\,\sigma(j):l(\rho)\leq j\leq l(\rho)+K-1\,\}\]这种设计使得模型在训练初期($\rho$ 较小)主要学习低PPL的“简单”提示,随着训练进行,逐渐转向高PPL的“困难”提示。

相对熵加权
该组件旨在缓解因专注于简单提示而可能导致的“熵崩溃”(即模型变得过于自信,失去探索能力)问题。
-
序列熵计算:对于每个生成序列 $o_i$,计算其平均Token熵 $\bar{H}_i$。
\[\bar{H}_{i}=\bar{H}(o_{i}\mid x)=\frac{1}{ \mid o_{i} \mid }\sum_{t=1}^{ \mid o_{i} \mid }H_{t}\] -
相对权重分配:计算当前批次内所有序列的平均熵 $\bar{H}$,然后为每个序列 $i$ 分配一个相对权重 $w_i$。
\[w_{i}=\frac{\bar{H}_{i}}{\bar{H}}\]这个权重是尺度不变的,它放大了那些比批次平均水平更具不确定性(高熵)的序列的影响,同时抑制了那些过于自信(低熵)的序列。这样可以在PPL调度的过程中,依然鼓励模型进行探索。
目标函数
PREPO将PPL调度和相对熵加权整合到策略梯度目标函数中。其最终的优化目标如下:
\[\mathcal{L}_{\text{PREPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{I}_{\rho}} \left[ \frac{1}{M} \sum_{i=1}^{M} w_i \sum_{t=0}^{ \mid o_i \mid -1} \min\left(s_{i,t}(\theta)\hat{A}_{i,t}, \text{clip}(s_{i,t}(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_{i,t}\right) \right]\]其中:
- $\mathcal{I}_\rho$ 是经过PPL调度选择的提示子集。
- $w_i$ 是第 $i$ 个序列的相对熵权重。
- $s_{i,t}(\theta)$ 是重要性采样比率。
- $\hat{A}_{i,t}$ 是优势函数估计。
通过这种方式,PREPO在宏观上(提示层面)遵循从易到难的课程,在微观上(序列层面)则鼓励对不确定路径的探索,从而实现了高效且稳健的学习。
实验结论
本文在Qwen和Llama系列多个模型上,针对数学推理任务进行了广泛实验,以验证PREPO方法的有效性。
主要结果
实验结果表明,PREPO在显著减少训练数据(rollouts)的同时,保持了与基线相当甚至更好的性能。
- 数据效率提升:与随机选择20%数据的基线相比,PREPO在不同模型上均实现了显著的rollout数量削减。例如,在Qwen2.5-Math-1.5B模型上减少了\(3倍\)(63.3%),在Llama3.1-8B上减少了\(2倍\)(48.9%),普遍将rollout需求降低了2到3倍。
- 性能表现:尽管使用了更少的数据,PREPO在AIME、MATH-500等多个数学推理基准测试上,其passrate@16的性能与使用更多数据的基线(如Random、GRESO)持平,甚至在某些情况下更优。
Qwen系列模型性能对比 (%)
| 模型 | 方法 | AIME25 | AIME24 | MATH500 | Olympiad | 平均 pass@16 | Rollouts |
|---|---|---|---|---|---|---|---|
| Qwen-M-1.5B | SFT | 1.46 | 5.31 | 63.35 | 33.09 | 25.80 | – |
| + Random | 6.98 | 15.28 | 75.70 | 38.47 | 34.39 | 716K | |
| + GRESO | 9.22 | 10.83 | 77.20 | 41.13 | 34.59 | 680K | |
| + PREPO | 13.04 | 16.09 | 76.30 | 39.85 | 36.32 | 263K | |
| Qwen-M-7B | SFT | 1.88 | 2.97 | 27.85 | 27.41 | 15.03 | – |
| + Random | 15.42 | 16.67 | 76.25 | 30.50 | 35.86 | 3.0M | |
| + GRESO | 15.38 | 10.83 | 75.40 | 24.17 | 34.16 | 2.5M | |
| + PREPO | 14.58 | 16.67 | 76.25 | 32.17 | 34.92 | 1.8M | |
| Qwen3-4B | SFT | 1.56 | 3.70 | 20.70 | 39.56 | 16.38 | – |
| + Random | 10.00 | 18.33 | 77.80 | 39.88 | 39.45 | 905K | |
| + GRESO | 18.33 | 25.83 | 77.80 | 26.83 | 37.46 | 654K | |
| + PREPO | 22.50 | 26.15 | 78.20 | 41.58 | 42.11 | 569K | |
| Qwen2.5-7B | SFT | 30.00 | 53.33 | 94.10 | 52.67 | 57.53 | – |
| + Random | 60.00 | 70.00 | 96.00 | 59.33 | 71.33 | 553K | |
| + GRESO | 56.67 | 69.17 | 96.40 | 57.33 | 69.89 | 472K | |
| + PREPO | 60.83 | 70.83 | 96.20 | 59.33 | 71.80 | 233K |
Llama模型性能对比 (%)
| 模型 | 方法 | GSM8K | MATH500 | 平均 pass@16 | Rollouts |
|---|---|---|---|---|---|
| Llama3.1-8B | SFT | 9.53 | 6.05 | 7.79 | – |
| + Random | 46.63 | 14.60 | 30.61 | 266K | |
| + GRESO | 41.77 | 16.80 | 29.29 | 273K | |
| + PREPO (Ours) | 49.80 | 18.00 | 33.90 | 136K |
消融研究与分析
-
组件贡献:消融研究证实,PPL调度和相对熵加权均对最终效果有贡献。仅使用PPL调度的版本性能已优于基线,而完整的PREPO方法(加入相对熵加权)则能获得进一步的稳定提升。
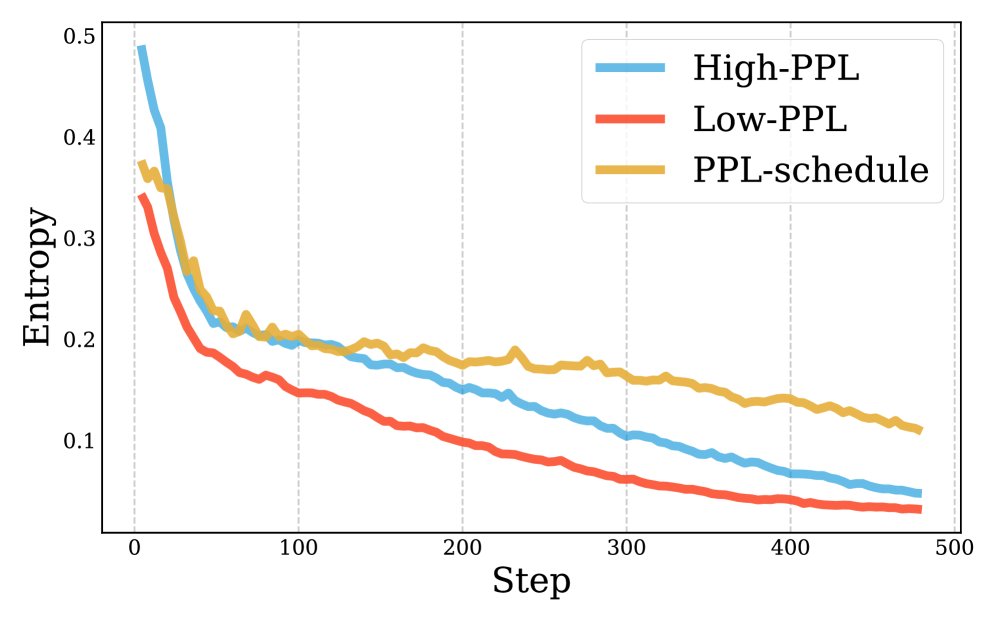
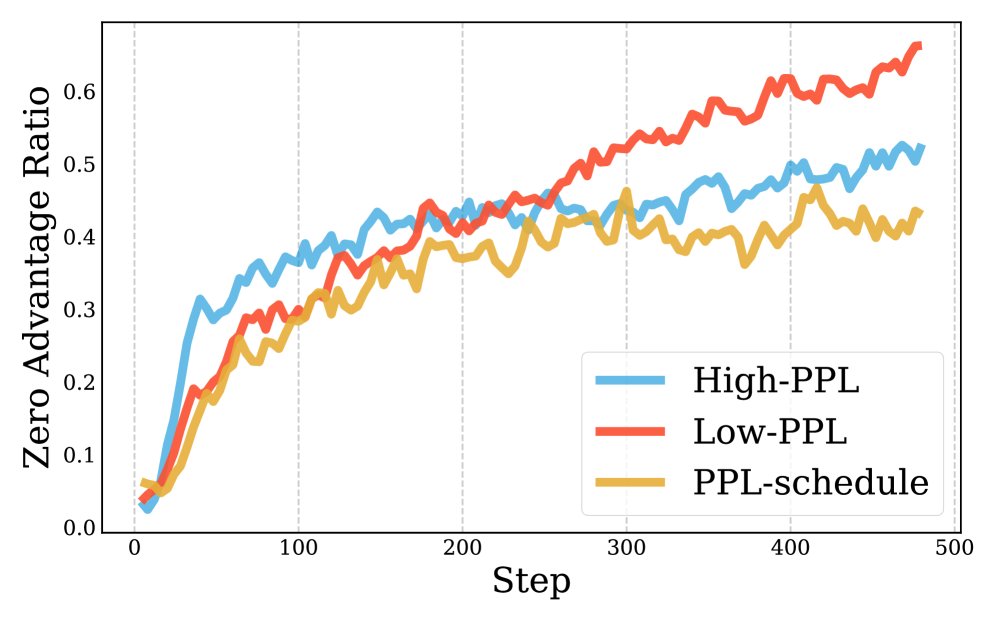 PPL调度(蓝色曲线)相比静态选择(仅低PPL或仅高PPL)能更好地维持探索(熵衰减更慢)并提高梯度有效性(零优势比例更低)。
PPL调度(蓝色曲线)相比静态选择(仅低PPL或仅高PPL)能更好地维持探索(熵衰减更慢)并提高梯度有效性(零优势比例更低)。 -
机制分析:分析表明,相对熵加权能有效降低“零优势比例”(zero-advantage ratio),这意味着更多样本为模型提供了有意义的梯度信号,从而提升了样本效率。
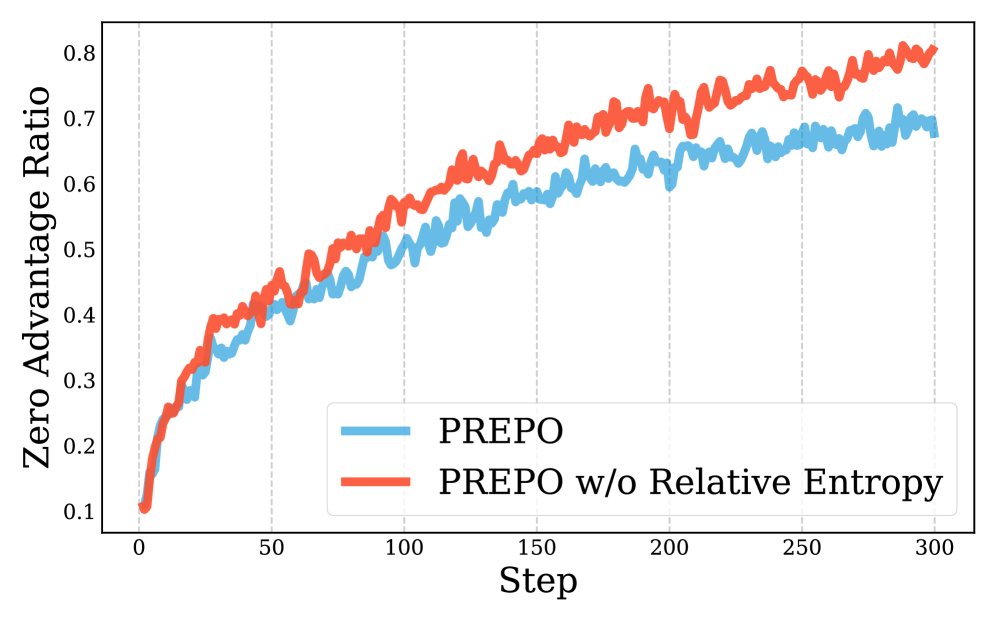 加入相对熵加权的PREPO(红色)比仅PPL调度(蓝色)的零优势比例更低。
加入相对熵加权的PREPO(红色)比仅PPL调度(蓝色)的零优势比例更低。 -
其他优点:PREPO的计算开销极小,不影响训练速度;它能促使模型学习更多样化类型的问题;并且实验证明,性能的提升来源于泛化推理能力的增强,而非对训练数据的死记硬背。
总结
实验结果有力地证明,通过利用困惑度和熵这两种内在数据属性,PREPO能够有效指导RLVR的训练过程,在大幅降低计算成本的同时,保证甚至提升了模型的推理性能,为大语言模型的高效强化学习提供了一条简单而有效的路径。