RL训练的秘密：LLM学会了举一反三，为何却被“先易后难”的结构卡住？

我们都知道，强化学习（RL）是提升大模型推理能力的一剂“猛药”。但它究竟是如何起作用的？仅仅是让模型能处理更长、更复杂的任务序列吗？还是说，它教会了模型一种更根本的能力——像搭乐高一样，将已知的小技能组合成全新的解决方案？

ArXiv URL：http://arxiv.org/abs/2512.01775v1

最近，普林斯顿大学的一项研究深入“解剖”了RL训练过程，试图揭开这个谜团。研究发现，RL不仅能让模型处理更长的问题，更重要的是，它确实能引导模型学会组合泛化（compositional generalization）。

然而，研究也揭示了一个令人意外的瓶颈：模型的学习能力，与其说受问题长度影响，不如说被问题的“结构”死死卡住。这究竟是怎么回事？

解构推理：从表达式到“模式树”

为了精确研究模型的推理过程，研究者选择了一个绝佳的实验场：Countdown任务。

任务很简单：给定$n$个数字和一个目标值，你需要用这些数字和四则运算（$+,-,\times,\div$）构造一个表达式，使其结果等于目标值。

这个任务的巧妙之处在于，任何一个解（比如 $8+(2\times 9)\div 3$）都可以被唯一地解析成一棵“表达式树”。通过规范化处理，这棵树可以对应到一个唯一的、抽象的计算模式（Canonical Pattern），如下图所示。

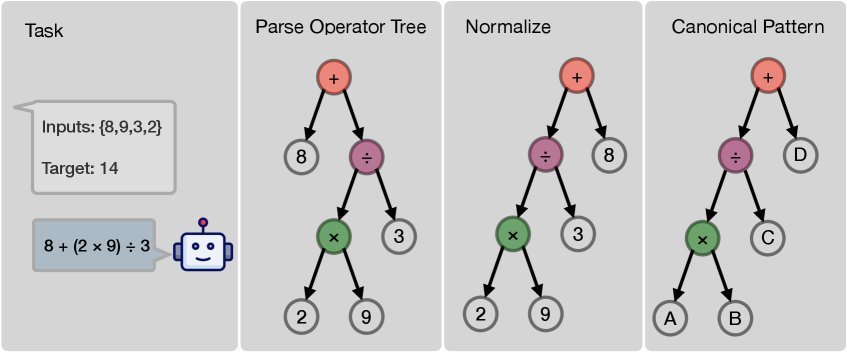
从表达式到模式树

图1：从模型生成的表达式到唯一的“计算模式”。这使得研究者可以精确分析模型采用的推理结构。

有了这个框架，我们就能清晰地区分两种泛化能力：

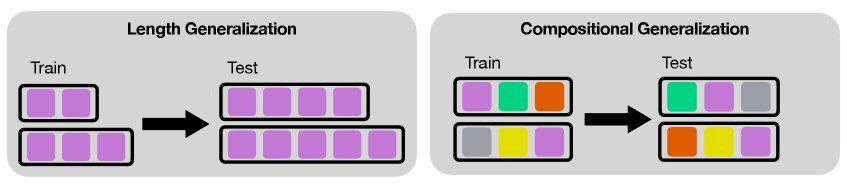
两种泛化能力

图2：长度泛化关注“量”的增加，而组合泛化关注“结构”的创新。

为了确保实验的严谨性，研究团队还精心设计了数据集生成方法，保证了所有计算模式的出现频率大致均匀，从而排除了数据偏见对“模式难度”判断的干扰。

长度不再是瓶颈，结构才是

研究者使用Qwen2.5系列模型（1.5B, 3B, 7B）在仅包含$n=3$和$n=4$（即3个或4个数字）的Countdown任务上进行RL微调。

结果首先证实了模型的长度泛化能力。只见过$n=3,4$问题的模型，在面对从未见过的$n=5$问题时，准确率（Pass@32）能达到近70%，在$n=6$问题上也能达到40%左右。

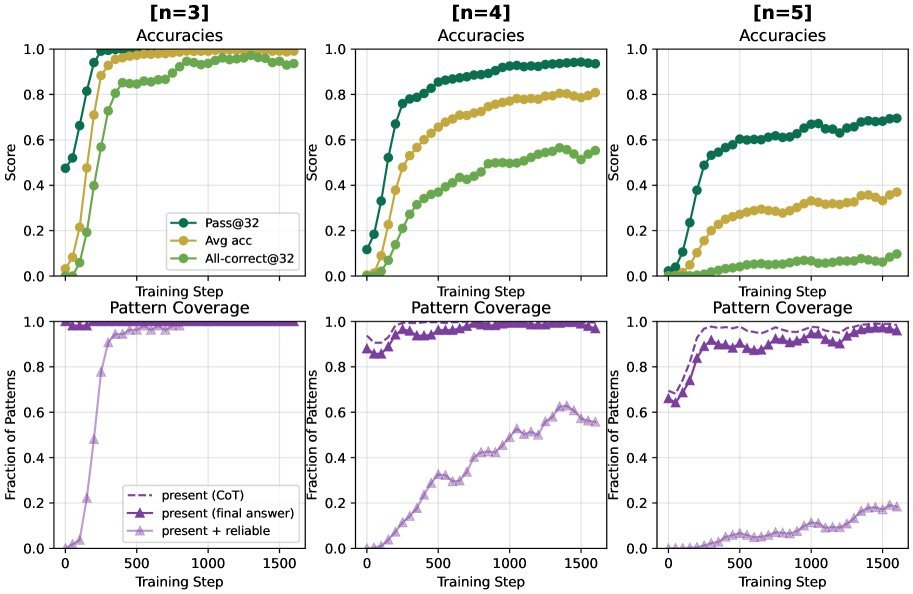
模型在不同长度任务上的表现

图3：模型在$n=5,6$的未见任务上表现出色，证明了长度泛化能力。

然而，当我们深入分析模型对不同“计算模式”的掌握情况时，一个更深层次的规律浮现了：决定任务难度的，根本不是问题长度，而是计算模式的结构！

如下图所示，在$n=4$的任务中，模型学习不同模式存在明显的先后顺序：

令人惊讶的是，这种难度层级在泛化到$n=5$的任务时依然存在。这说明，结构复杂度才是限制模型推理能力的真正瓶颈。

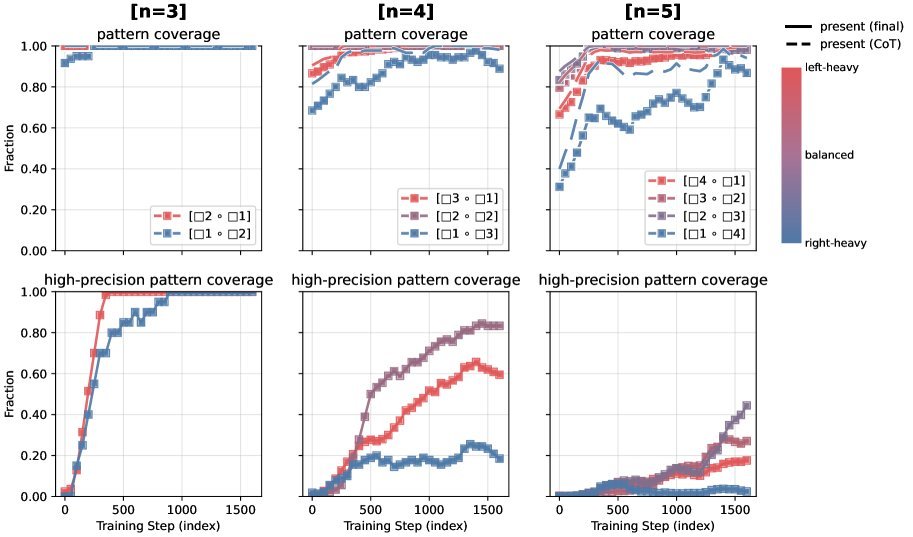
模式结构决定学习难度

图4：无论问题长度如何，模型总是先学会平衡结构（紫色），再学不平衡结构（红/蓝）。

“前瞻瓶颈”：先易后难的诅咒

更有趣的现象发生在同样深度、同样长度的不平衡结构之间。研究发现，右重结构（right-heavy，如 $[1]\circ[3]$，对应 $A\circ(B\circ C\circ D)$）比左重结构（left-heavy，如 $[3]\circ[1]$，对应 $(A\circ B\circ C)\circ D$）要难得多！

为什么会这样？

研究者将其归因于自回归模型固有的“前瞻瓶颈”（Lookahead Bottleneck）。

对于左重结构 $(A\circ B\circ C)\circ D$，模型可以先处理简单的子问题 $(A\circ B\circ C)$，再将其结果与 $D$ 结合。这是一个“先难后易”的过程。

但对于右重结构 $A\circ(B\circ C\circ D)$，模型必须在生成序列的早期就定下第一个运算符 $\circ$，然后再去解决后面那个复杂的子问题 $(B\circ C\circ D)$。这要求模型具备强大的“规划能力”，在未完全探索复杂部分之前就做出关键决策。

这种“先易后难”的结构，对自回归模型来说是一个巨大的挑战，导致其在右重结构上表现脆弱。

真正的“无中生有”：RL学会了组合新技能

为了验证RL是否能真正教会模型“创造”新技能，研究者进行了一项堪称严苛的实验。他们在训练数据中，完全移除了某个$n=3$的模式（$A/B+C$）及其所有$n=4$的衍生模式（如 $A/B+C+D$ 等）。

结果令人振奋：模型在训练后，不仅成功“重构”出了被移除的$n=3$模式，还进一步泛化，掌握了其更复杂的$n=4$衍生模式！

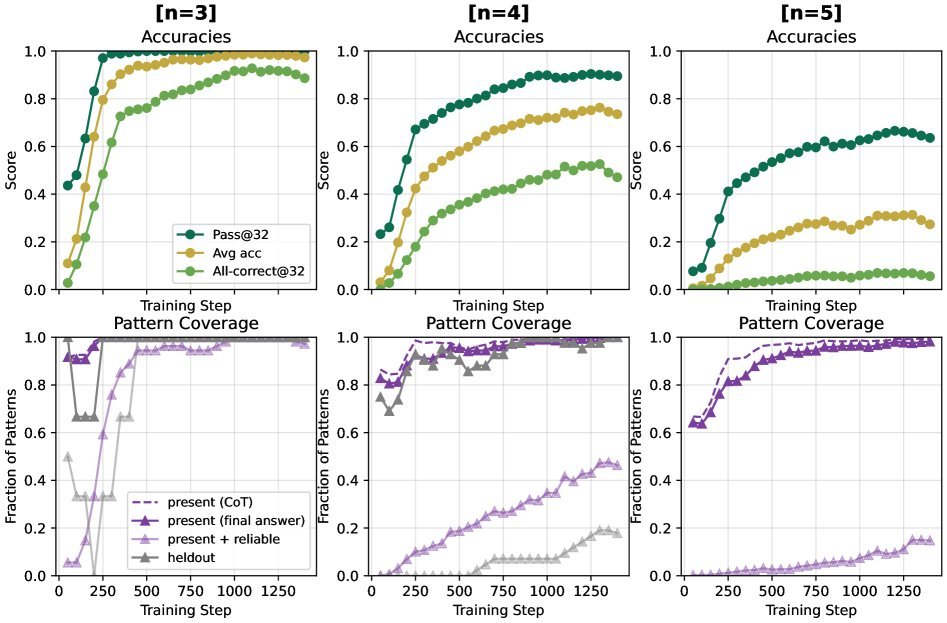
模型泛化到未见过的模式家族

图5：模型成功恢复了在训练中被完全移除的模式家族，证明了其组合新技能的能力。

这个实验强有力地证明了，RL不仅仅是在“锐化”模型对已知路径的认知，而是在实实在在地教会模型如何将学到的小技能（如计算 $A/B$）与其它技能（如计算 $X+C$）组合起来，从而解决从未见过的、结构全新的问题。

RL为何优于SFT？

研究还对比了强化学习（RL）与监督微调（Supervised Fine-tuning, SFT）的效果。结果显示，SFT模型即使在有思维链（CoT）的情况下，也远远不及RL模型，尤其在向更长的$n=5$任务泛化时表现很差。

这表明，RL的“探索-利用”机制比SFT的“模仿学习”更能有效地激发模型的组合泛化潜力。

结论

这项研究为我们揭示了RL训练LLM推理能力的深刻机制：

  1. 结构为王：决定推理难度的不是问题长度，而是其内在的“计算模式”结构。

  2. 前瞻瓶颈：“先易后难”的右重结构是自回归模型的一个根本性弱点，限制了其组合能力。

  3. RL激发创造：RL能够引导模型超越模仿，学会“无中生有”地组合技能，实现真正的组合泛化。

这些发现不仅加深了我们对LLM推理机制的理解，也为未来的模型训练提供了宝贵的启示。或许，我们不应再盲目地用“更长更难”的数据去训练模型，而是应该设计一套针对“结构瓶颈”的课程，通过引入少量但结构复杂的关键样本，更高效地推动模型推理能力的边界。