告别炼丹玄学:谷歌用概率统一AI Agent,提出“自由度”新思路

AI Agent的浪潮正席卷而来,从能自主思考和使用工具的ReAct,到分工协作的多智能体(Multi-Agent)系统,各种新架构层出不穷。然而,这个繁荣的背后也隐藏着一个巨大的挑战:我们如何科学地比较这些设计?一个ReAct Agent和一个多智能体系统,哪个更优?我们是该优化提示词,还是该引入更复杂的控制流程?
ArXiv URL:http://arxiv.org/abs/2512.04469v1
过去,Agent的设计更像一门“炼丹玄学”,依赖直觉和大量的经验试错。现在,来自Google Cloud的研究者们提出了一套统一的数学框架,试图将这门艺术转变为一门严谨的工程科学。他们认为,无论Agent的架构多么复杂,其本质都可以被描述为一个概率过程。
这篇论文的核心洞见是:任何Agent的目标,都是在给定初始上下文 $c$ 的情况下,最大化一系列“正确”动作 $\mathbf{a}_g$ 出现的概率。有了这个统一的视角,我们终于有了一把衡量所有Agent设计的“标尺”。
万物皆可概率:Agent的统一数学语言
让我们把Agent的复杂行为简化一下。它的每一步,都是在当前状态 $s_{i-1}$ 下,选择一个动作 $a_i$。这个过程本身就充满了不确定性。这篇研究巧妙地将其建模为一个概率链:
\[P(\mathbf{a} \mid c)=P(a_{n} \mid s_{n-1},c)P(a_{n-1} \mid s_{n-2},c)\dots P(a_{1} \mid s_{0},c)\]这个公式看起来可能有点吓人,但它的意思很简单:整个动作序列 $\mathbf{a}$ 发生的总概率,等于每一步选择正确动作的概率的连乘积。
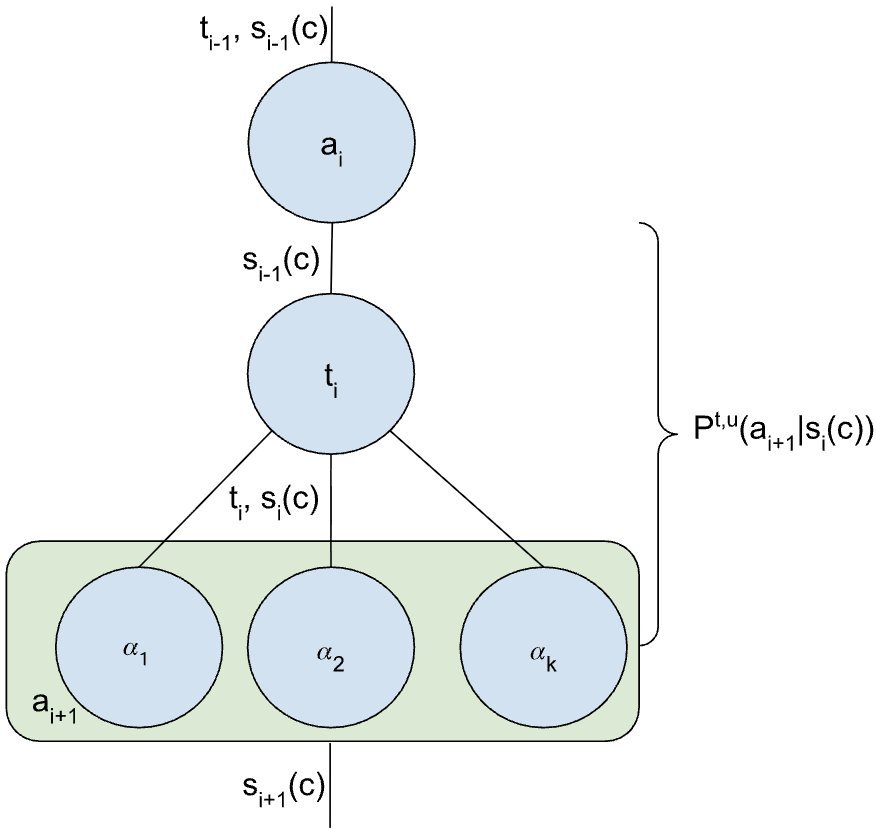
Agent设计师的终极目标,就是想尽办法让这个总概率 $P(\mathbf{a} \mid c)$ 最大化。而不同的Agent策略,如ReAct、控制流或多智能体,其实是在用不同的方式“操纵”这个概率链。
用概率解构ReAct:”思考“的价值是什么?
ReAct是目前最经典的单Agent范式之一,它通过“思考(Thought)-行动(Action)”循环来完成任务。那么,在概率框架下,“思考”这一步究竟起到了什么作用?
该研究指出,“思考” $t_i$ 的本质,是为了提升模型在当前状态 $s_{i-1}$ 下选择正确动作 $a_i$ 的概率。用公式表达就是,它将原本的 $P(a_i \mid s_{i-1})$ 分解为了两步:
\[P^{t}(a_{i} \mid s_{i-1})=P(a_{i} \mid t_{i},s_{i-1})P(t_{i} \mid s_{i-1})\]模型首先生成一个最有帮助的“思考” $t_i$,然后基于这个思考去选择动作 $a_i$。这就像解数学题时,先写下解题思路再动笔计算,可以大大提高正确率。所以,CoT(Chain-of-Thought)和ReAct的有效性,在这里得到了清晰的数学解释。
核心概念:“自由度”(Degrees of Freedom)
这篇论文引入了一个极其重要的概念——自由度(Degrees of Freedom)。它指的是在设计和优化一个Agent时,我们可以调控的“杠杆”或“旋钮”。
-
对于一个基础的ReAct Agent,我们的自由度相对有限。我们能优化的主要是:
-
初始状态 $s_0$:通过提示词工程(Prompt Engineering)来优化。
-
状态更新函数 $u$:决定如何将新信息(如工具返回结果)整合到历史记录中。
-
推理功能 $\mathcal{F}$:这通常与底层LLM模型本身有关,比如通过微调来改变它。
-
这些杠杆虽然有效,但它们是“静态”的,一旦设定就不易在任务执行中动态改变。
多智能体系统:解锁全新的“自由度”
多智能体系统(Multi-Agent Systems, MAS)的威力在哪里?这套框架给出了一个漂亮的答案:它引入了全新的、动态的自由度。
想象一个任务被拆分给两个Agent协作完成。Agent 1执行一系列动作 $\mathbf{a}_L$ 后,需要把它的成果传递给Agent 2。这个“传递”过程,就不是一个简单的信息复制,而是一个可以被优化的概率事件:$P(c_L \mid \mathbf{a}_L)$。
这个公式 $P(c_L \mid \mathbf{a}_L)$ 代表了什么?它代表了Agent 1在完成自己的子任务 $\mathbf{a}_L$ 后,生成一个“最佳上下文” $c_L$ 给Agent 2的概率。
这正是“协作”的数学本质!Agent之间可以通过沟通、协商、甚至“讨价还价”,来动态地寻找一个最优的上下文 $c_L$,从而最大化下游Agent成功的概率。这相当于在系统运行时,增加了一个强大的动态调优旋钮,这是单个Agent所不具备的。
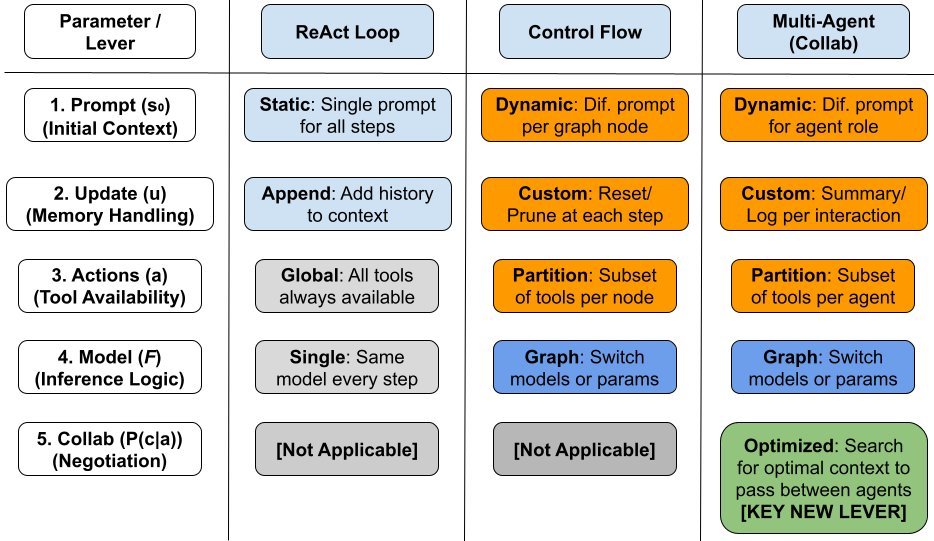
上图直观地展示了不同策略的“自由度”差异。
-
单体架构(Monolithic,如ReAct):自由度被“锁定”,主要依赖于初始设定。
-
控制流(Control Flow):通过预设的图或状态机,可以动态地改变状态 $s$ 或推理功能 $\mathcal{F}$,增加了灵活性。
-
多智能体(Multi-Agent):不仅拥有前两者的自由度,更解锁了独一无二的协作(Collaboration)维度,即优化跨Agent的上下文传递概率 $P(c \mid a)$。
平衡理论与现实:别忘了“协作成本”
当然,更多的自由度也意味着更高的复杂性。多智能体间的通信和协商会带来额外的延迟、计算和Token消耗,这就是协作成本(Collaboration Cost)。
一个负责任的框架必须考虑这些现实因素。因此,研究者提出了一个带有正则项的优化目标:
\[\text{Maximize}\left(P(...)-\lambda\cdot\text{CollabCost}(\cdot)\right)\]这里的 $\lambda$ 是一个平衡系数,它确保我们在追求最高成功概率的同时,也兼顾系统的效率和成本。这使得整个框架从一个纯理论模型,走向了具有现实指导意义的工程蓝图。
结论:从“炼丹”到“工程”
这篇来自Google Cloud的论文,为当前略显“混沌”的AI Agent领域带来了一缕清风。它没有提出一个全新的、更强的Agent模型,而是提供了一套更根本的东西:一个统一的、严谨的数学语言。
通过将Agent行为统一到概率框架下,并引入“自由度”这一核心概念,该研究清晰地揭示了不同Agent架构(如ReAct与多智能体)之间的本质区别和各自的优化潜力。它让我们明白,多智能体系统的强大之处,并不仅仅是“人多力量大”,而在于它通过“协作”这一独特机制,解锁了全新的、可在运行时动态优化的概率杠杆。
这项工作标志着AI Agent设计正从一门经验性的“艺术”,向一门可量化、可分析的“工程学”迈出坚实的一步。未来,基于这个框架,我们或许能开发出更智能的算法,让Agent系统能自主地探索和利用这些“自由度”,从而在通往更高性能的道路上自我进化。