Sampling and Loss Weights in Multi-Domain Training

TL;DR

本文提出，在多领域训练中，应将传统的单域权重分解为两个互补的角色：用于提升泛化能力的损失权重 (loss weights)和用于降低梯度方差、加速优化的采样权重 (sampling weights)，并为它们分别设计了估计算法。

相关工作

当前，大规模模型（如 LLM）的成功严重依赖于在海量、异构的数据集上进行训练，这些数据来自维基百科、GitHub 等多个领域 (domain)。这些领域在数据质量、噪声水平和信息多样性上存在显著差异。

普遍的做法是为每个领域分配一个固定的标量权重，然后在这个混合体上进行训练。这种“单权重”方法简单有效，但它模糊了权重的两个根本不同的作用：

  1. 目标影响：一个领域对最终学习目标的贡献程度，这应取决于其数据的可靠性和泛化能力。
  2. 采样频率：在随机优化过程中从一个领域采样数据的频率，这应取决于其梯度特性以提高优化效率。

本文旨在解决这一问题，通过解耦这两种权重，分别研究并提出实用的估计算法，以期在不进行显式领域自适应的情况下，同时改善模型的泛化性能和优化效率。

本文方法

本文的核心思想是将领域权重分解为损失权重和采样权重两个维度，并分别对其进行优化。

概念框架

  1. 损失权重 (\(w\))：这类权重直接作用于经验风险最小化 (Empirical Risk Minimization, ERM) 的目标函数中。它们调整了每个领域的经验风险对总损失的贡献。直观地说，更可靠、噪声更低的领域应该被赋予更高的权重，以减小泛化差距。其目标函数形式为：

    \[\hat{\mathcal{L}}_{\mathcal{S},\pi,w}(\theta)\;=\;\sum_{i=1}^{K}\pi_{i}w_{i}\,\hat{\mathcal{L}}_{\mathcal{S}_{i}}(\theta)\]

    其中 \(π\) 是给定的领域重要性先验，\(w\) 是待优化的损失权重。

  2. 采样权重 (\(b\))：这类权重决定了在构建每个小批量 (mini-batch) 时，从各个领域中抽取的样本数量 \(b_i\)。其主要目标是降低随机梯度估计的方差，从而加速模型收敛。梯度方差更大的领域应该被更多地采样。

损失权重的估计算法

1. 线性回归下的洞察与 One-shot FGLS

在线性回归的设定下，本文从广义最小二乘法 (Generalized Least Squares, GLS) 理论出发。Aitken 定理表明，最优的权重与数据标签的噪声方差成反比：

\[w_{i}^{\star}\propto\frac{1}{\sigma_{i}^{2}}\]

传统的做法（可行广义最小二乘法，FGLS）需要多次迭代训练来估计噪声方差 \(σ_i^2\)，计算成本高昂且在过参数化时可能失效。

为解决此问题，本文提出了 One-shot FGLS 算法。该方法在训练过程中动态调整损失权重：

2. 通用模型下的 ERMA

为了将此思想推广到任意模型，本文提出了一种基于最小化泛化上界的 ERMA (Empirical Risk Minimization with Adaptation) 更新规则。该方法通过一个动态公式来调整损失权重：

\[w_{i}^{(t+1)}\propto w_{i}^{(t)}\exp\left(\gamma_{1}\,\pi_{i}G(t)\,\mathcal{L}_{i}(\theta_{t})-\gamma_{2}\,\pi_{i}w_{i}^{(t)}\,\operatorname{Var}_{i}(\theta_{t})\right)\]

此更新规则会根据每个领域在当前模型下的损失和方差，自适应地调整其权重。

采样权重的估计算法：VA

采样权重的目标是最小化小批量梯度估计的方差。梯度估计的总方差可以表示为：

\[\mathbb{E}\Bigl[\,\bigl\ \mid g_{t}-\nabla_{\theta}\hat{\mathcal{L}}_{\mathcal{S}}(\theta_{t})\bigr\ \mid ^{2}\,\Bigr]=\sum_{i=1}^{K}\frac{\pi_{i}^{2}w_{i}^{2}}{b_{i}}\,v_{i}^{2}\]

其中 \(b_i\) 是从领域 \(i\) 采样的数量，\(v_i^2\) 是领域 \(i\) 内的梯度方差。

通过求解一个约束优化问题（在总批量大小 \(B\) 固定的情况下最小化上述方差），可以得到最优的采样数量 \(b_i\)：

\[b_{i}\;\propto\;\pi_{i}w_{i}v_{i}\]

基于此，本文提出了 VA (Variance-Aware Sampling) 方案。该方案在训练过程中：

实验结论

本文通过在线性回归、逻辑回归以及一个简单的神经网络（在MNIST上）进行实验，以验证所提方法的有效性。

实验设置

实验通过人工方式构建了多个领域，这些领域在数据协方差 (\(C_i\))、标签噪声 (\(p_i\) 或 \(σ_i^2\)) 等方面存在差异，以模拟真实世界的多领域异构性。

关键结果

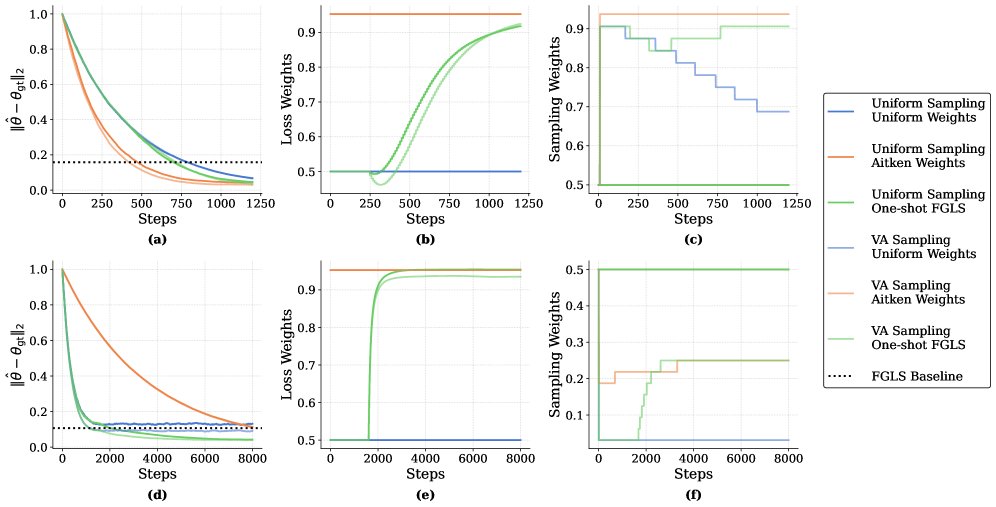图1：线性回归实验结果。上排 \((C1, C2) = (100, 1)\)，下排 \((C1, C2) = (1, 100)\)。可以看到 One-shot FGLS（损失权重）和 VA（采样权重）都比基线方法（Uniform）收敛得更快，误差更低。

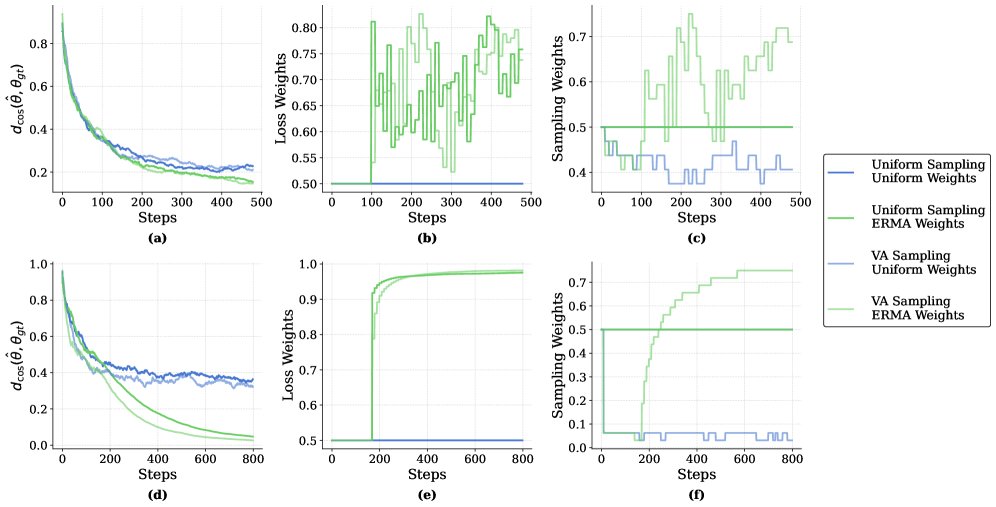图2：逻辑回归实验结果。与线性回归类似，ERMA（损失权重）和 VA（采样权重）均展现出优势，并且它们的组合（ERMA+VA）通常能取得最佳或接近最佳的性能，证明了它们的互补性。

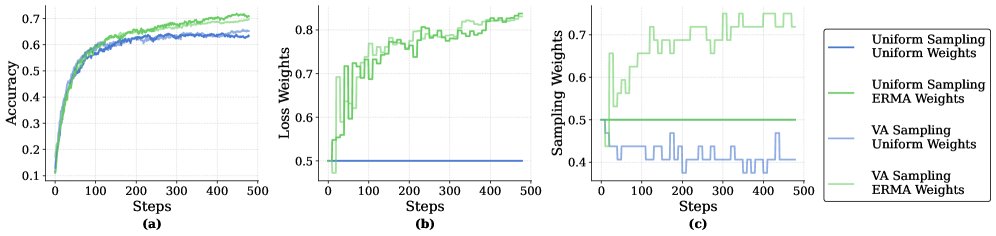图3：神经网络（MNIST）实验结果。在此设置下，ERMA（损失权重）取得了最佳效果，显著优于均匀加权。然而，VA（采样权重）几乎没有带来改善。作者推测，这是因为在该任务中，干净领域和噪声领域的数据输入高度相似，导致它们之间的梯度方差差异不显著，VA 无法发挥作用。

最终结论