Scaling Latent Reasoning via Looped Language Models
-
ArXiv URL: http://arxiv.org/abs/2510.25741v2
-
作者: Kai Hua; Jiajun Shi; Jiaheng Liu; Enduo Zhao; Jian Yang; Ziniu Li; Lu Li; Bohong Wu; Tianle Cai; Xun Zhou; 等30人
-
发布机构: ByteDance; Carnegie Mellon University; Conscium; M-A-P; Mila - Quebec AI Institute; Peking University; Princeton University; University of California, Santa Cruz; University of Manchester; University of Montreal; University of Pennsylvania
好的,我将以世界顶级AI研究科学家的身份,遵循您的指示,撰写这份论文笔记。
TL;DR
本文提出了一种名为Ouro的循环语言模型(Looped Language Model, LoopLM),通过在预训练阶段引入潜在空间中的迭代计算,使得1.4B和2.6B参数的小模型能够达到比自身大2-3倍的SOTA模型(最高12B)的性能,从而开辟了一条提升模型参数效率的全新扩展路径。
关键定义
本文提出或沿用了以下关键概念:
- 循环语言模型 (Looped Language Model, LoopLM): 一种在单次前向传播中,递归地、多次应用同一组共享参数的Transformer层的模型架构。这种设计将计算深度与参数数量解耦,实现了在不增加模型大小的情况下深化计算。
- 自适应计算 (Adaptive Computation): 模型根据输入样本的复杂性,动态决定执行多少次循环计算的能力。这通过一个可学习的“提前退出”门控机制实现,简单任务消耗更少计算,复杂任务则分配更多计算。
- 熵正则化目标 (Entropy-Regularized Objective): 一种创新的训练目标函数,它在标准的下一词元预测损失之外,增加了一个关于“退出步数”概率分布的熵项。该正则项旨在防止模型在训练中倾向于总是使用最大循环次数,鼓励其根据输入难度探索不同的计算深度。
- 聚焦自适应门控训练 (Focused Adaptive Gate Training): 在预训练之后的一个专门阶段,冻结语言模型的参数,仅训练退出门控机制。此阶段的目标是让门控的决策(即决定在第几步退出循环)与每一步循环带来的实际性能提升对齐,从而在计算开销和模型精度之间做出更优的权衡。
相关工作
当前,大语言模型(LLMs)的发展主要依赖于扩大模型尺寸、数据量和计算资源,但这导致部署成本高昂、延迟增加且可及性受限。因此,在固定的参数预算内提升模型能力,即提高参数效率,变得至关重要。
现有的提升参数效率的方法主要有两个方向:一是增加训练数据量,但面临数据稀缺的瓶颈;二是在推理时通过思维链(Chain-of-Thought, CoT)等方式增加计算量,但这会增加输出序列的长度。
本文旨在解决的核心问题是:如何在不显著增加模型参数数量的前提下,提升模型的推理和知识运用能力? 具体而言,本文探索能否将“推理过程”内化到模型的预训练阶段,通过在潜在空间中进行迭代计算,而非生成冗长的显式文本(如CoT),来构建更高效、更强大的语言模型。
本文方法
LoopLM 架构
本文提出的Ouro模型家族基于循环语言模型(LoopLM)架构。与标准的Transformer模型堆叠L个独立的层(参数为$\theta_1, \dots, \theta_L$)不同,LoopLM重复使用一个包含L个共享参数层的块$\mathcal{M}^L$。
一个标准的L层Transformer模型可以表示为:
\[F(\cdot) := \mathrm{lmhead} \circ \mathcal{M}^{L} \circ \mathrm{emb}(\cdot), \quad \mathcal{M}^{L}(\cdot) := \mathcal{T}_{\theta_{L}} \circ \cdots \circ \mathcal{T}_{\theta_{1}}(\cdot)\]而LoopLM则将这个块$\mathcal{M}^L$迭代应用$t$次:
\[F^{(t)}(\cdot) = \mathrm{lmhead} \circ \underbrace{\mathcal{M}^{L} \circ \mathcal{M}^{L} \circ \cdots \circ \mathcal{M}^{L}}_{t \text{ iterations}} \circ \mathrm{emb}(\cdot)\]其中,$t$是循环步数。当$t=1$时,该模型等价于标准Transformer。这种循环结构允许模型通过增加循环次数$t$来加深计算图,而不是通过增加物理层数来增加参数。在每个循环步$t$,模型都会产生一个输出,其对应的损失为$\mathcal{L}^{(t)}$。
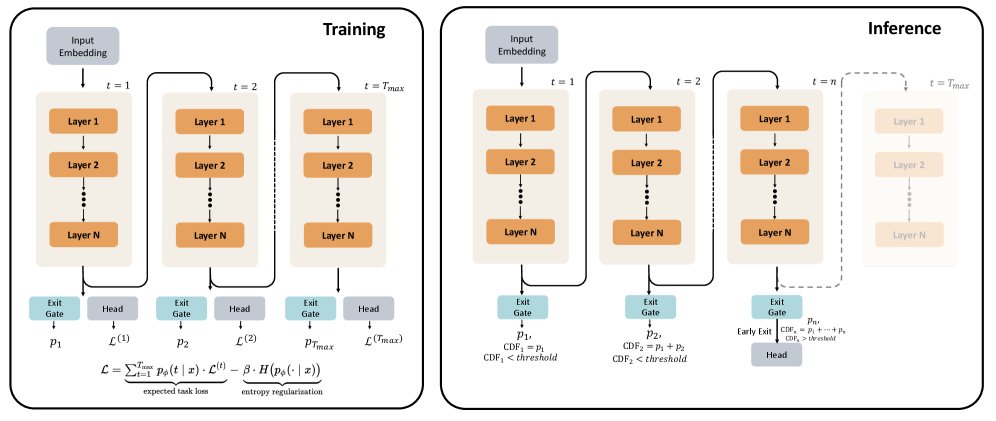
自适应计算与门控机制
为了让模型能根据输入难度自适应地选择循环步数$t$,本文引入了一个提前退出门控机制。在每个循环步 $t$ (当 $t \leq T_{\max}$),一个门控网络会并行计算一个即时退出概率 $\lambda_t(x)$:
\[\lambda_t(x) = \sigma(\mathrm{Linear}_{\phi}(h^{(t)})) \in (0, 1)\]其中 $h^{(t)}$ 是第$t$步的最终隐藏状态,$\phi$是门控的参数。
模型在第 $t$ 步退出的(归一化)概率 $p_\phi(t \mid x)$ 由此导出。在推理时,给定一个阈值 $q \in [0, 1]$,模型会在累积退出概率首次超过 $q$ 的那一步 $t_{\mathrm{exit}}(x)$ 停止计算并输出结果,从而实现计算资源的动态分配。
两阶段训练策略
为了有效训练LoopLM及其自适应门控,本文设计了一个两阶段的训练流程。
阶段一:熵正则化预训练
在预训练阶段,为了避免模型简单地学习到总是使用最大循环次数(因为更深的计算通常会带来更低的单步损失),本文引入了一个熵正则化的目标函数:
\[\mathcal{L} = \underbrace{\sum_{t=1}^{T_{\max}} p_{\phi}(t \mid x) \, \mathcal{L}^{(t)}}_{\text{预期任务损失}} - \underbrace{\beta \, H(p_{\phi}(\cdot \mid x))}_{\text{熵正则化项}}\]该损失函数由两部分组成:
- 预期任务损失:将每一步的损失 $\mathcal{L}^{(t)}$ 按该步的退出概率 $p_\phi(t \mid x)$ 加权求和。
- 熵正则化项:$H(\cdot)$ 是退出概率分布的熵,$\beta$ 是一个超参数。这一项惩罚过于集中的概率分布,鼓励模型探索不同的计算深度。
从变分推断的角度看,这个目标等价于在一个隐变量模型中最大化证据下界(ELBO),其中隐变量是退出步数,其先验分布被设定为均匀分布。均匀先验是无偏的,它将决定计算深度的任务完全交给模型根据输入难度来判断。
阶段二:聚焦自适应门控训练
在第一阶段之后,语言模型的参数被冻结,只对退出门控的参数 $\phi$ 进行微调。此阶段的目标是让门控的决策更“聪明”,即只有当增加一次循环能带来足够大的性能提升时,才选择继续循环。
具体方法是,首先计算从 $t-1$ 步到 $t$ 步的实际损失改进量 $I_i^{(t)}$。然后,基于这个改进量与一个阈值 $\gamma$ 的比较,生成一个“理想”的继续/退出标签 $w_i^{(t)}$。最后,使用标准的二元交叉熵损失 $\mathcal{L}_{\text{adaptive}}$ 来训练门控,使其预测的继续概率 $(1-\lambda_i^{(t)})$ 接近这个理想标签 $w_i^{(t)}$。这个过程强迫门控学会了如何在计算成本和性能收益之间进行权衡。
整体训练流程
Ouro模型的训练分为多个阶段,总共使用了7.7T tokens。 
-
架构与数据:模型基于标准的Decoder-only Transformer,使用RoPE、SwiGLU和RMSNorm。训练数据涵盖了网页文本、数学、代码和长文本等,全部来自开源数据集。
-
多阶段训练:
- 预训练(Pre-training):使用6T tokens,主要为网页数据,辅以代码和数学数据,构建模型基础能力。
- 持续训练(Continual Training):使用1.4T tokens更高质量的数据,提升模型能力。
- 长上下文训练(LongCT):使用20B tokens的长文本数据,将模型上下文能力扩展到64K。
- 中期训练(Mid-training):使用高质量的问答和思维链数据,进一步开发高级能力。
- 推理SFT(Reasoning SFT):最终进行监督微调,得到推理增强版的模型。
下面是Ouro模型架构和预训练配方的概览表格。
| 模型 | 参数 | 层数 | 隐藏层大小 | MHA头数 | FFN中间层大小 | 词表大小 |
|---|---|---|---|---|---|---|
| Ouro-1.4B | 1.4B | 24 | 2048 | 16 | 5632 | 49152 |
| Ouro-2.6B | 2.6B | 32 | 2560 | 32 | 6912 | 49152 |
| 阶段 | 初始学习率 | 衰减学习率 | tokens数量(T) | 序列长度(K) | 全局批次大小(M tokens) |
|---|---|---|---|---|---|
| Stage 1 (Warmup) | $3.0\times 10^{-4}$ | - | 0.05 | 4 | 4 |
| Stage 1 (Stable) | $3.0\times 10^{-4}$ | - | 6.0 | 4 | 4 |
| Stage 2 (CT Anneal) | $3.0\times 10^{-5}$ | $3.0\times 10^{-6}$ | 1.4 | 16 | 4 |
| Stage 3 (LongCT) | $3.0\times 10^{-5}$ | $3.0\times 10^{-6}$ | 0.02 | 64 | 4 |
| Stage 4 (Mid-training) | $1.0\times 10^{-5}$ | $1.0\times 10^{-6}$ | 0.1 | 4 | 4 |
实验结论
尽管完整的实验部分未提供,但根据引言和贡献部分的总结,可以得出以下关键结论:
- 显著的参数效率提升:经过7.7T tokens的预训练后,1.4B和2.6B参数的Ouro模型在广泛的基准测试中,其性能表现与参数量高达4B、8B甚至12B的SOTA标准Transformer模型相当。这证明LoopLM架构带来了2-3倍的参数效率增益,对于资源受限的部署环境至关重要。
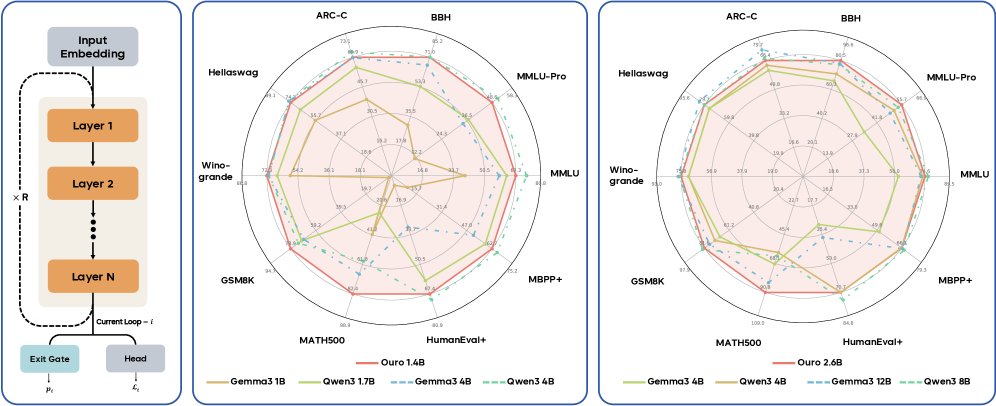
- 增益来源是知识操纵能力:通过受控实验发现,循环计算并没有增加模型的原始知识存储容量(循环和非循环模型每个参数约存储2比特信息),而是显著增强了其知识操纵(knowledge manipulation)能力,特别是在需要事实组合和多跳推理的复杂任务上。
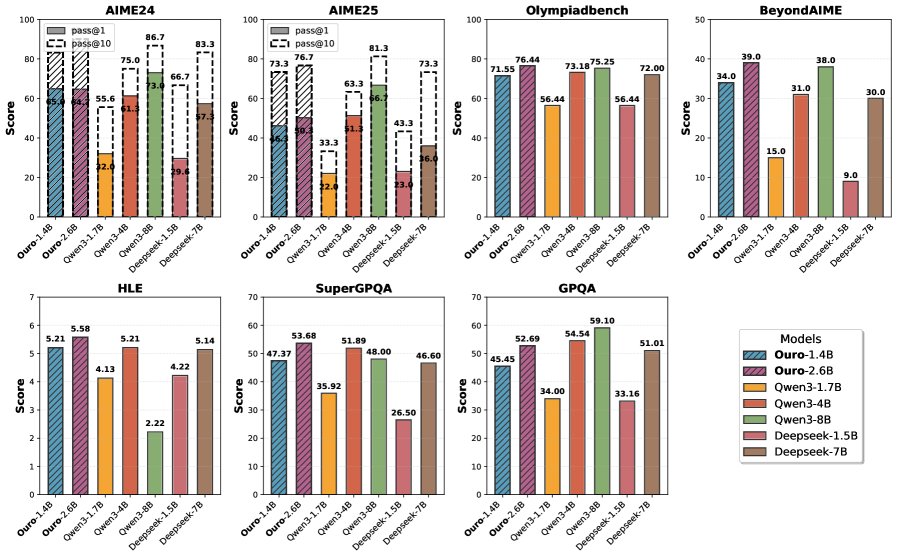
- 更忠实的推理轨迹:与生成显式文本的CoT相比,LoopLM在潜在空间中通过迭代更新生成的“推理轨迹”与最终的输出结果更加一致。这表明其推理过程更具因果忠实性,而不是事后合理化(post-hoc rationalization)。
- 安全性的提升:在HEx-PHI等安全性基准上,LoopLM的有害性更低。并且,随着循环步数的增加(包括外推到训练时未见的步数),模型的安全性也随之提高。
- 最终结论:本文的研究成功确立了循环深度(loop depth)作为模型尺寸和数据量之外的第三个有效的扩展轴。Ouro模型的成功表明,Looped Language Model是进入推理时代后,一个极具潜力的、用于构建更强大、更高效基础模型的新方向。