Shrinking the Variance: Shrinkage Baselines for Reinforcement Learning with Verifiable Rewards

• ArXiv URL: http://arxiv.org/abs/2511.03710v1

• 作者: Andrea Zanette; Zhaoyi Zhou; Guanning Zeng; Daman Arora

• 发布机构: Carnegie Mellon University

---

TL;DR

本文提出了一种基于收缩估计 (shrinkage estimators) 的新型基线 (baseline) 方法，通过在统计上更优地结合单个提示 (per-prompt) 和跨提示批次 (across-prompt) 的奖励均值，来显著降低策略梯度估计的方差，从而为大型推理模型的强化学习训练带来更强的稳定性与性能。

关键定义

本文的核心方法建立在对强化学习中基线方法的统计学再思考之上，关键定义如下：

1. 带可验证奖励的强化学习 (Reinforcement Learning with Verifiable Rewards, RLVR): 一种针对大型推理模型（LRMs）的训练范式。在该范式中，模型根据稀疏的、基于规则的标量奖励进行优化，这些奖励明确地指示模型最终答案的正确性（例如，数学问题回答正确奖励为1，错误为0）。
2. 基线 (Baseline): 在策略梯度方法中，为了降低梯度估计器的方差而从奖励中减去的一项。它是一个与状态（在本文中是提示 \(prompt\)）相关的标量值 \(b(x)\)，理想的基线应能在不引入梯度偏差的前提下最小化方差。其最优选择通常是状态值函数 \(μ(x)\)。
3. 收缩估计器 (Shrinkage Estimator): 一种统计估计方法，它通过将单个独立的估计值（如单个提示的样本均值）“收缩”或拉向一个共同的中心值（如整个批次的全局均值），来提高整体估计精度。这种方法通过引入少量偏置来换取方差的大幅降低，从而获得更低的总均方误差 (MSE)。
4. James-Stein (JS) 基线: 本文提出的具体基线方法。它应用了 James-Stein 收缩原理，为每个样本计算一个基线。该基线是“单个提示的留一法均值”和“跨提示的批次均值”的加权平均。为了确保策略梯度的无偏性，该方法在计算均值和收缩系数时均采用了精巧的留一法 (leave-one-out) 构造。

相关工作

当前，使用策略梯度方法（如 REINFORCE、GRPO）进行 RLVR 训练是提升大型推理模型能力的主流技术之一。然而，这些方法普遍面临策略梯度估计器方差过高的问题，这会导致训练过程不稳定，收敛困难。

为了解决这一问题，研究者们引入了基线 (baseline) 来降低方差。现有方法主要分为两类：

1. 经典强化学习方法: 引入一个辅助的神经网络来学习和近似值函数 (value function)。这种方法虽然有效，但显著增加了模型的复杂性、超参数调优的难度以及训练和维护的成本。
2. 近期针对推理模型的方法: 放弃使用额外的网络，直接利用蒙特卡洛采样得到的奖励来构造基线。典型做法是使用每个提示 (per-prompt) 下多次生成结果的奖励经验均值作为基线（如 GRPO、RLOO）。这种方法简单、无偏，但当每次采样的数量（rollouts）较少时，其估计的方差依然很大，存在改进空间。

本文旨在解决上述第二类方法中，因采样数量少而导致的基线估计不准、梯度方差过高的问题。通过引入统计学中的收缩估计原理，本文提出了一种更精确的基线估计方法，以在不增加计算开销和超参数的情况下，更有效地降低梯度方差。

本文方法

本文方法的核心在于，将估计一组基线的问题视为一个经典的“联合估计多个均值”的统计问题，并为此引入了 James-Stein (JS) 收缩估计器。

理论推导：从梯度方差到基线均方误差

策略梯度 \(g\) 的方差可以表示为其协方差矩阵的迹，等价于估计的均方误差 $\mathrm{Var}[g]=\mathbb{E}\left[\ \mid g(\mathbf{x},\mathbf{Y};\theta)-\nabla_{\theta}J(\theta)\ \mid ^{2}\right]$。为了最小化此方差，需要选择最优的基线 \(b\)。在忽略得分函数（score function）范数影响的常见简化下，最优基线 \(b(x)\) 就是能最小化奖励预测误差的真实值函数 $\mu(x) = \mathbb{E}_{y\sim\pi_{\theta}(\cdot\mid x)}[r(x,y)]$。 因此，降低策略梯度方差的问题，转化为如何更准确地估计值函数 $\mu(x)$ 的问题，即最小化基线的均方误差 (MSE)：

\[\mathbb{E}[(b(x)-\mu(x))^{2}] = \mathrm{Var}[b(x)] + (\text{Bias}[b(x)])^2\]

创新点：引入收缩估计实现偏置-方差权衡

在RLVR的实践中，通常会有一个批次 \(n\) 个不同的提示，每个提示生成 \(m\) 个回答。对于每个提示 \(i\) 的值函数 $\mu_i$，存在两种极端的估计方法：

1. 单个提示均值 (Per-prompt mean): $\widehat{\mu}_i=\frac{1}{m}\sum_{j=1}^{m}r_i^j$。这是对 $\mu_i$ 的无偏估计，但当 \(m\) 很小时，其方差很大。
2. 全局批次均值 (Global batch mean): $\widehat{\bar{\mu}}=\frac{1}{nm}\sum_{i=1}^{n}\sum_{j=1}^{m}r_i^j$。该估计的方差较小，但当不同提示的真实值函数 $\mu_i$ 差异较大时，会引入巨大的偏置。

本文的洞察在于，根据 James-Stein 悖论，当同时估计多个均值时，独立的经验均值并非最优解。通过将各个提示的均值向全局均值“收缩”，可以获得整体上更低的均方误差。因此，本文提出了一个插值形式的收缩估计器：

\[b_{i}^{j,\mathrm{JS1}}=(1-\lambda)\,\widehat{\mu}_{i}+\lambda\,\widehat{\bar{\mu}}\]

其中，收缩系数 $\lambda \in [0,1]$ 控制着偏置与方差之间的权衡。

最终方法：确保无偏性的 James-Stein 基线

直接使用上述 \(b_i^{j,JS1}\) 会引入梯度偏差，因为基线的计算依赖于用于计算梯度的奖励 \(r_i^j\)。为解决此问题，本文设计了一种精巧的双重留一法 (two-level leave-one-out) 构造，以确保基线与对应奖励的独立性。

对于每个样本 $(x_i, y_i^j)$，其基线 $b_i^j$ 的计算步骤如下：

1. 计算留一法单个提示均值 (Leave-one-out prompt-level mean)：不使用当前奖励 $r_i^j$，只用同提示下的其他奖励计算均值。

\[\widehat{\mu}_{i}^{-j} :=\frac{1}{m-1}\sum_{j^{\prime}\neq j}r_{i}^{j^{\prime}}\]

1. 计算留一法全局批次均值 (Leave-one-out batch-level mean)：不使用当前提示 \(i\) 的任何信息，只用批次内其他提示的均值来计算全局均值。

\[\widehat{\bar{\mu}}_{-i} :=\frac{1}{n-1}\sum_{k\neq i}\widehat{\mu}_{k} \quad (\text{其中 } \widehat{\mu}_{k}=\frac{1}{m}\sum_{j=1}^{m}r_k^j)\]

1. 估计最优收缩系数 $\widehat{\lambda}_i$：系数的估计也基于留一法数据，以避免信息泄露。

\[\widehat{\lambda}_{i}=\frac{n-1}{n}\cdot\frac{\widehat{v}_{-i}}{\widehat{v}_{-i}+\widehat{s}_{-i}}\]

其中，$\widehat{v}_{-i}$ 估计了提示内奖励的平均方差（鼓励收缩），$\widehat{s}_{-i}$ 估计了不同提示真实值函数之间的离散度（抑制收缩）。

1. 构建最终的 James-Stein 基线:

\[b_{i}^{j}=(1-\widehat{\lambda}_{i})\,\widehat{\mu}_{i}^{-j}+\widehat{\lambda}_{i}\,\widehat{\bar{\mu}}_{-i}\]

这个最终的基线 $b_i^j$ 在构造上与 $r_i^j$ 无关，因此保证了策略梯度的无偏性。

优点

• 更低的梯度方差: 理论上可证明，该方法能得到比单独使用单个提示均值或全局均值更低的基线MSE，从而降低策略梯度的方差。
• 即插即用: 该方法是现有无评判员（critic-free）RL算法（如RLOO, GRPO）的直接替代品，无需修改模型架构或增加任何新的超参数。
• 计算高效: 所有计算都基于批次内的奖励样本，计算开销极小。

实验结论

本文在数学推理和逻辑谜题推理两大类任务上，对提出的 James-Stein (JS) 基线和标准的 RLOO 基线（即仅使用留一法单个提示均值）进行了对比实验。实验算法基于 GRPO（不带优势归一化，等价于 RLOO）。

数学推理

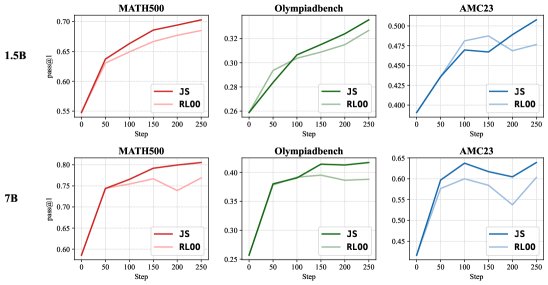
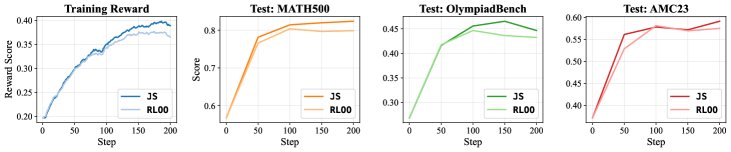
• 设置: 使用 Qwen 系列数学模型在 DAPO17k 和 MATH12k 数据集上进行训练，在 MATH500、OlympiadBench 等基准上进行评测。
• 结果: JS 基线方法在不同模型和评测基准上均显著优于 RLOO 基线，带来了 1.1% 到 4.3% 的准确率提升。训练曲线显示，JS 基线下的模型奖励提升速度也明显更快。

在 Qwen2.5 数学模型上，JS 基线（绿色）相较于 RLOO 基线（蓝色）在多个测试集上均取得显著性能优势。

在 Qwen3-4B-Base 模型上，JS 基线不仅训练奖励（左图）上升更快，在测试集上的准确率（右图）也持续领先。

逻辑谜题推理

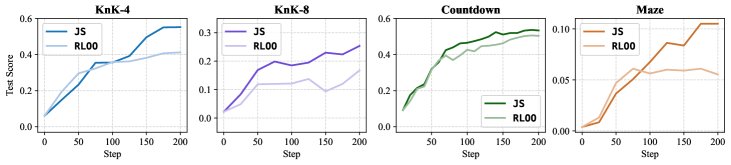
• 设置: 在骑士与无赖（Knights-and-Knaves）、倒计时（Countdown）和迷宫（Maze）等多种逻辑谜题上，使用 Qwen 和 Mistral 系列模型进行实验。
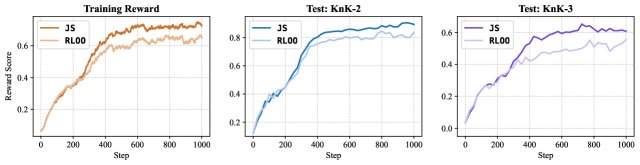
• 结果: JS 基线在各项任务和模型上均表现出优越性。特别是在一个对 Qwen2.5-1.5B 进行的长达 1000 步的训练实验中，JS 基线不仅使训练奖励更快达到并维持在更高水平，其最终的测试准确率也显著高于 RLOO 基线，进一步验证了其稳定性和有效性。

在多种逻辑谜题任务上，JS 基线一致地超越了 RLOO 基线。

在骑士与无赖（KnK）任务的长期训练中，JS 基线（橙色）的训练奖励和测试准确率均稳定优于 RLOO 基线（蓝色）。

最终结论

实验结果有力地证实了理论分析：本文提出的 James-Stein 收缩基线通过更有效地降低策略梯度方差，能够带来更稳定的训练过程和更优的模型性能。作为一个无需调参、计算高效的即插即用模块，它为改进大型推理模型的强化学习训练提供了一个简单而强大的新工具。