Token级优化为何能对齐序列级奖励？阿里耗费数十万GPU时，揭秘LLM强化学习稳定之道

用强化学习（RL）来“调教”大模型，使其在复杂任务上表现更佳，已是行业共识。但一个棘手的问题始终困扰着研究者们：训练过程极其不稳定，常常像坐过山车。

ArXiv URL：http://arxiv.org/abs/2512.01374v1

这背后隐藏着一个根本矛盾：我们通常基于模型生成的完整序列（如一个完整的答案）给予奖励，但在优化时，却是在逐个Token的粒度上调整模型。

这种“序列级奖励”与“Token级优化”的错位，真的科学吗？它会不会就是导致训练不稳定的罪魁祸首？

来自阿里巴巴的研究者们，通过一篇新论文给出了一个深刻的数学解释。他们耗费了数十万GPU小时，在一个300亿参数的MoE模型上进行了详尽实验，不仅揭示了其中的原理，还提供了一套稳定RL训练的实用“配方”。

序列奖励 vs. Token优化：一个理论近似

直接优化期望的序列级奖励 $ \mathcal{J}^{\text{seq}}(\theta) $ 非常困难。因为一个长序列的生成概率 $ \pi_{\theta}(y \mid x) $ 往往是一个极小的数，这会导致梯度计算时出现巨大的数值范围和方差，让优化过程难以控制。

\[\nabla_{\theta}\,\mathcal{J}^{\text{seq}}(\theta) = \mathbb{E}_{y\sim\mu_{\theta_{\text{old}}}}\left[\frac{\pi_{\theta}(y \mid x)}{\mu_{\theta_{\text{old}}}(y \mid x)}\,R(x,y)\sum_{t=1}^{ \mid y \mid }\nabla_{\theta}\log\pi_{\theta}(y_{t} \mid x,y_{<t})\right]\]

这篇论文的核心洞见在于，它指出我们常用的Token级优化目标 $ \mathcal{J}^{\text{token}}(\theta) $，实际上是序列级目标 $ \mathcal{J}^{\text{seq}}(\theta) $ 的一种一阶近似。

\[\nabla_{\theta}\,\mathcal{J}^{\text{token}}(\theta)=\mathbb{E}_{y\sim\mu_{\theta_{\text{old}}}}\left[\sum_{t=1}^{ \mid y \mid }\frac{\pi_{\theta}(y_{t} \mid x,y_{<t})}{\mu_{\theta_{\text{old}}}(y_{t} \mid x,y_{<t})}\,R(x,y)\,\nabla_{\theta}\log\pi_{\theta}(y_{t} \mid x,y_{<t})\right]\]

简单来说，只有当目标策略 $ \pi_{\theta} $ 与采样策略 $ \mu_{\theta_{\text{old}}} $ 非常接近时，这两个目标的梯度才近似相等。这意味着，通过优化Token级目标，我们才能够有效地提升真正的序列级奖励。

逼近有效的两大基石

那么，如何保证这种“近似”是有效的呢？研究指出，关键在于最小化两个核心差异：

1. 训练-推理差异（Training-Inference Discrepancy）：即训练系统和推理引擎在计算上的细微差别。即使参数完全相同，这两个引擎的输出也可能不一致，尤其是在复杂的硬件和软件栈上。

2. 策略陈旧度（Policy Staleness）：在进行多次梯度更新时，用于采样数据的策略（旧策略 $ \theta_{\text{old}} $）和正在优化的策略（新策略 $ \theta $）之间的差距。差距越大，近似就越不成立。

\[\frac{\pi_{\theta}(y_{t} \mid x,y_{<t})}{\mu_{\theta_{\text{old}}}(y_{t} \mid x,y_{<t})}=\underbrace{\frac{\pi_{\theta_{\text{old}}}(y_{t} \mid x,y_{<t})}{\mu_{\theta_{\text{old}}}(y_{t} \mid x,y_{<t})}}\_{\text{训练-推理差异}}\times\underbrace{\frac{\pi_{\theta}(y_{t} \mid x,y_{<t})}{\pi_{\theta_{\text{old}}}(y_{t} \mid x,y_{<t})}}\_{\text{策略陈旧度}}\]

这个公式清晰地告诉我们，为了让Token级优化有效，必须同时控制好这两个“变量”。

MoE模型的特殊挑战与“路由回放”

对于混合专家模型（Mixture-of-Experts, MoE）来说，问题变得更加复杂。

MoE模型在生成每个Token时，都会动态地选择一部分“专家”来参与计算。这种动态的专家路由（Expert Routing）机制，为上述两个差异引入了新的变数。

例如，策略陈旧不仅体现在模型参数的变化，还体现在专家选择路径的改变上，这会急剧地放大策略间的差异。

为了解决这个问题，研究者引入了路由回放（Routing Replay）技术。其核心思想是在策略优化期间，固定住生成数据时所选择的专家路径，让MoE模型暂时像一个稠密模型一样被优化。

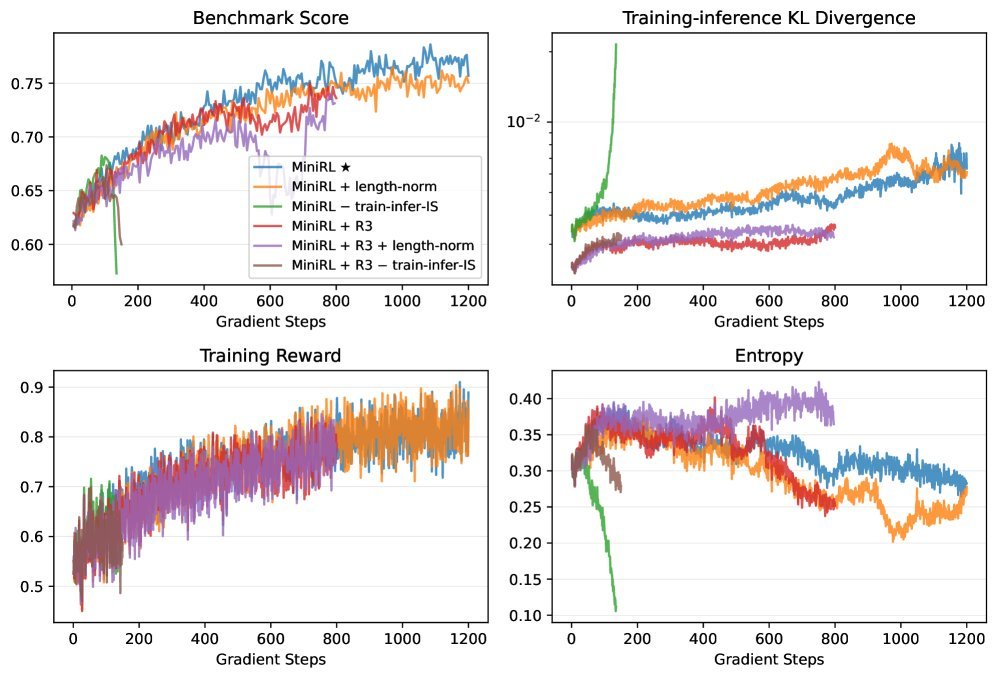
如上图所示，在On-policy（即每次更新都用新数据）训练中，遵循理论的基线方法（MiniRL）表现最为稳定。而移除重要性采样（wo/ train-infer-is）或引入不合理的长度归一化（w/ length-norm）都会破坏近似的有效性，导致训练崩溃。

实验验证：稳定才是硬道理

为了加速训练，我们通常会采用Off-policy的方式，即用一批数据进行多次梯度更新。但这会不可避免地增加“策略陈旧度”。实验结果表明，此时稳定训练的秘诀在于Clipping和路由回放的结合。

• Clipping：限制单步更新的幅度，直接控制策略陈旧度。

• 路由回放（Routing Replay）：通过固定专家路径，同时降低了训练-推理差异和策略陈旧度带来的不确定性。

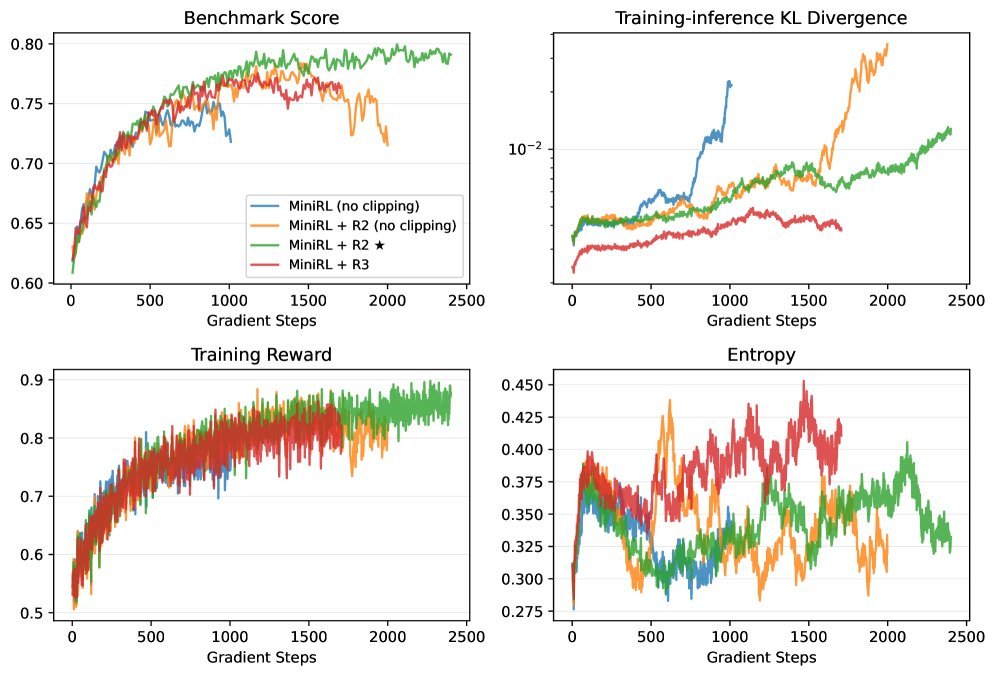
上图展示了在Off-policy（N=2，即每批数据更新2次）设定下，不同策略的稳定性。可以看到，简单的MiniRL（蓝色）很快就崩溃了。而结合了路由回放（R2/R3）和Clipping的策略（绿色和紫色）则表现出优异的稳定性，并取得了最好的性能。

当Off-policy的程度加剧（N=4或N=8），这种稳定性差异更加明显。

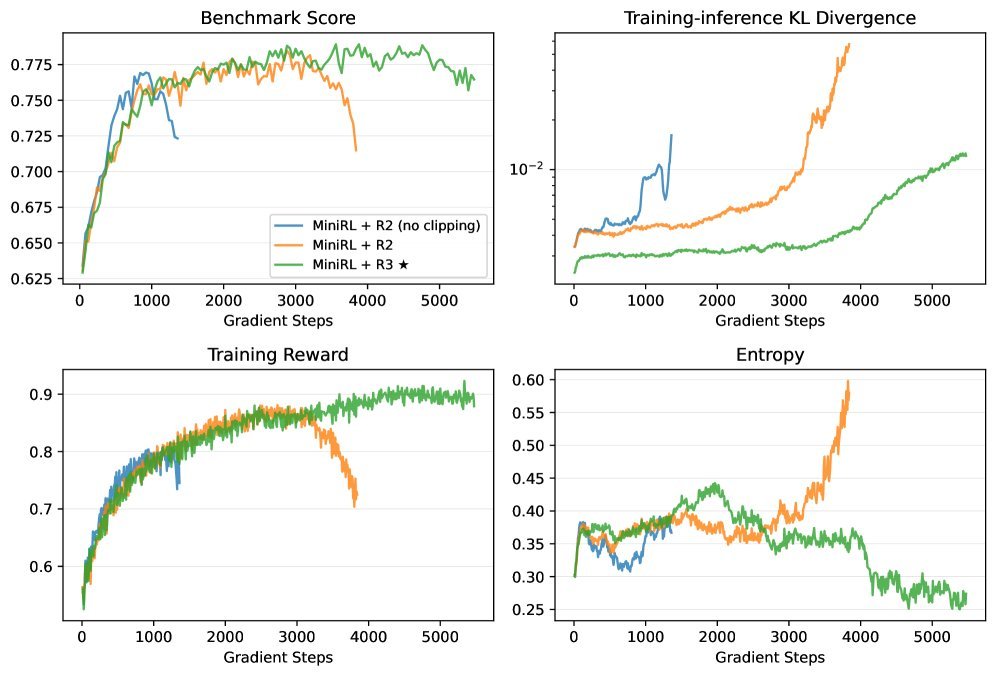
稳定训练的终极价值

这项研究还有一个非常振奋人心的发现：一旦找到了稳定的RL训练“配方”，模型的初始状态（冷启动）对最终性能的影响会大大减小。

研究者们用三个不同的前沿模型蒸馏出的数据作为冷启动，使用稳定的“MiniRL + R2”配方进行训练。

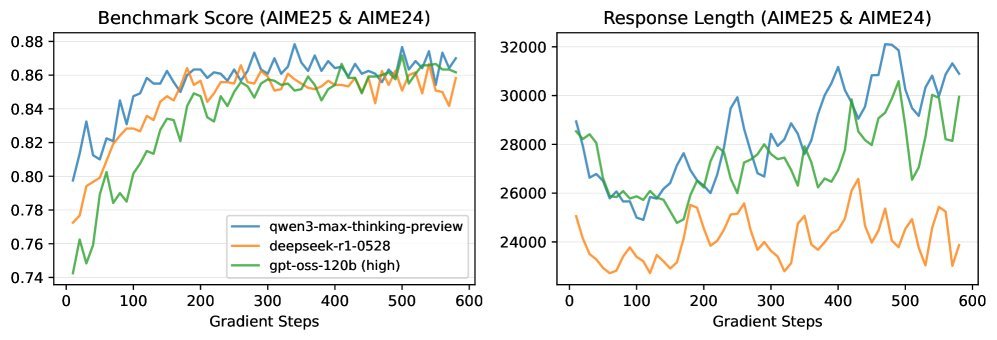
结果如上图所示，尽管起点不同，但经过足够长的稳定训练后，三个模型最终达到了非常接近的性能水平。

这意味着，未来的研究可以更专注于RL算法和训练过程本身，而不必过度纠结于“如何获得一个完美的SFT初始模型”。

结论

这篇论文为“用Token级优化实现序列级目标”这一RL for LLMs的普遍实践，提供了坚实的理论基础。它明确了训练稳定性的两个关键支柱：减小训练-推理差异和控制策略陈旧度。

通过在300亿MoE模型上进行的超大规模实验，该研究不仅验证了理论的正确性，还为业界提供了一套行之有效的稳定训练方案，特别是针对MoE模型的路由回放技术，展现了其在稳定训练中的关键作用。

稳定，是成功规模化RL的决定性因素。有了这份“稳定之道”的指引，我们离充分释放大模型潜力又近了一步。